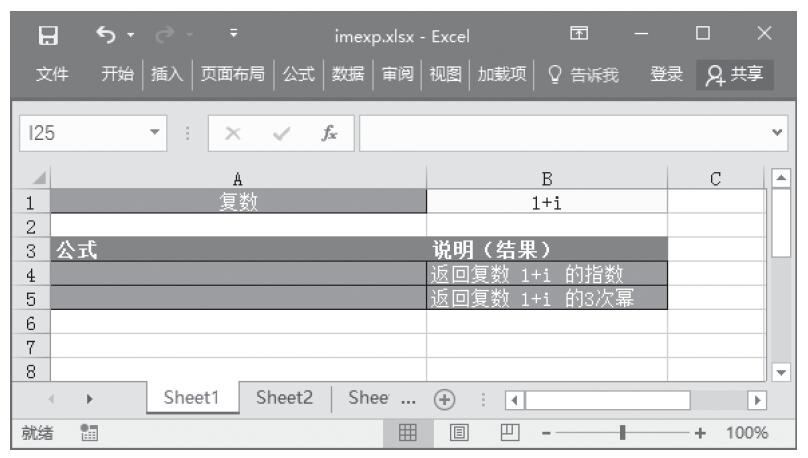
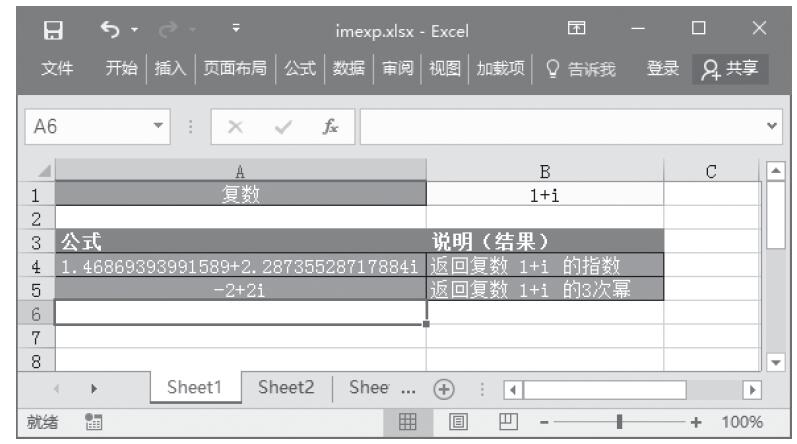
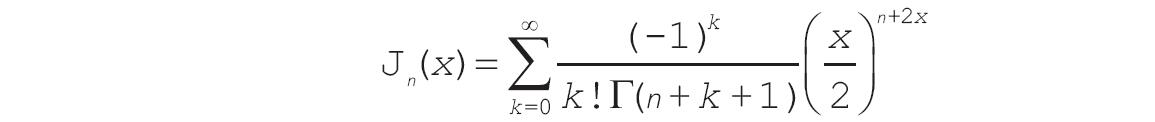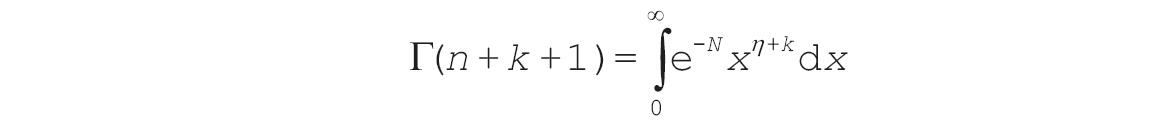GESTEP函数用于检验数字是否大于阈值。如果number大于等于step,返回1,否则返回0。使用该函数可筛选数据。例如,通过计算多个函数GESTEP的返回值,可以检测出数据集中超过某个临界值的数据个数。
GESTEP(number,step)
其中参数number为待测试的数值,step为阈值。如果省略step,则函数GESTEP假设其为零。
典型案例
检验数字是否大于阈值。本例的原始数据如图18-45所示。
步骤1:在单元格A2中输入公式“=GESTEP(8,7)”,用于检查8是否大于等于7。
步骤2:在单元格A3中输入公式“=GESTEP(8,8)”,用于检查8是否大于等于8。
步骤3:在单元格A4中输入公式“=GESTEP(-7,-8)”,用于检查-7是否大于等于-8。
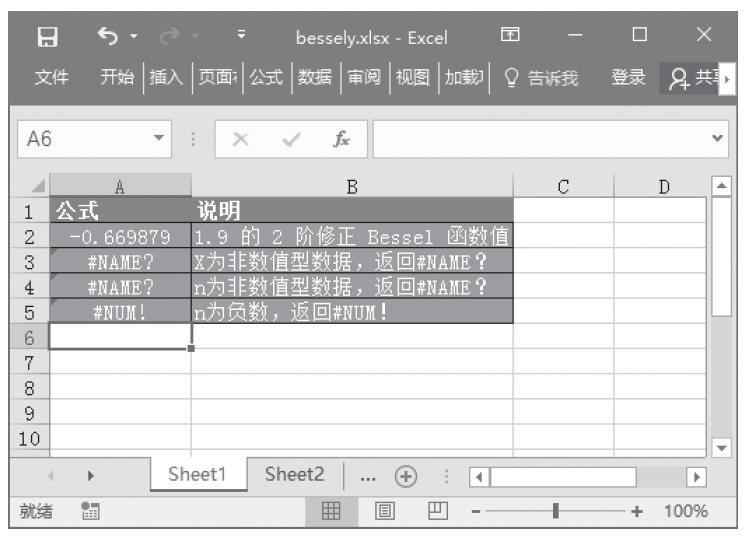
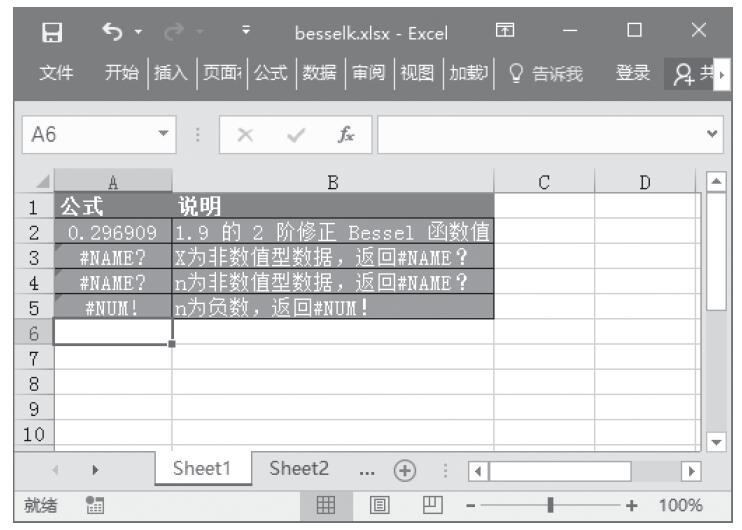
步骤4:在单元格A5中输入公式“=GESTEP(-1,0)”,用于检查-1是否大于等于0。最终计算结果如图18-46所示。
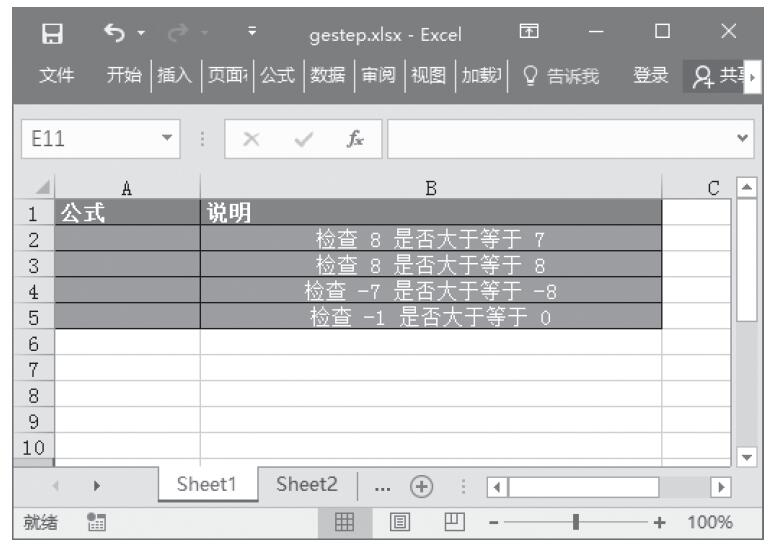
图18-45 原始数据
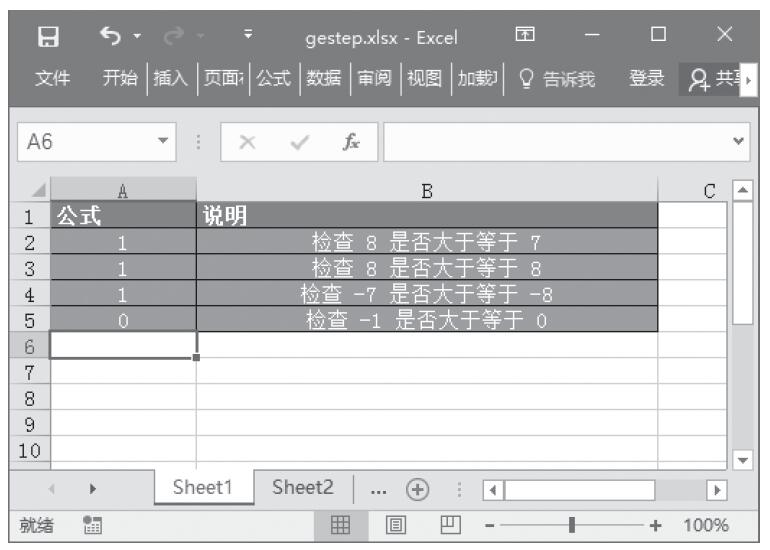
图18-46 计算结果
使用指南
如果任一参数为非数值,则函数GESTEP返回错误值“#VALUE!”。