Excel中提供了大量的数学与三角函数，以帮助用户提高运算效率。本章将介绍Excel 2016中数学与三角函数的用途、语法以及参数的详细说明，并结合实例介绍函数在实际中的应用。本章最后提供一个综合案例，以帮助读者理解数学与三角函数的具体用法。
ATANH函数的功能是计算参数的反双曲正切值，参数必须介于-1到1之间（除去-1和1）。ATANH函数的语法如下：
ATANH(number)
其中参数number为-1到1之间的任意实数。
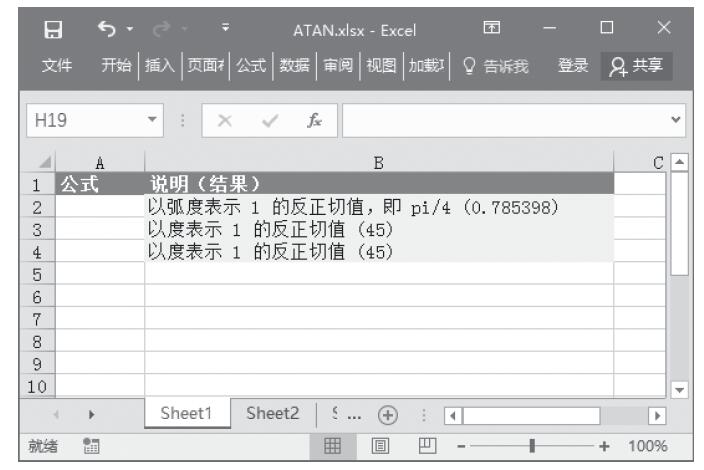
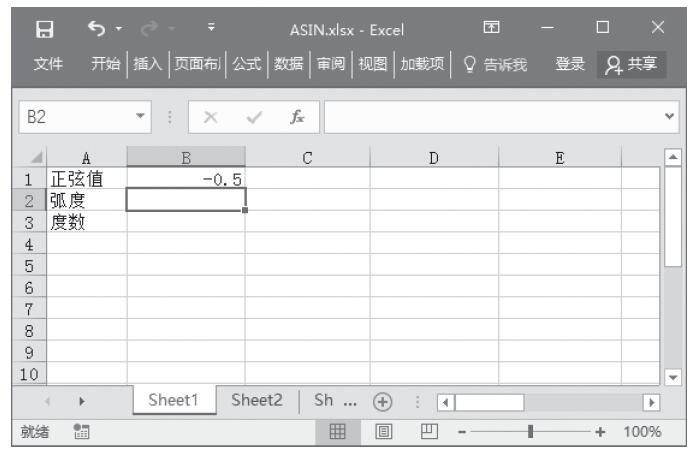
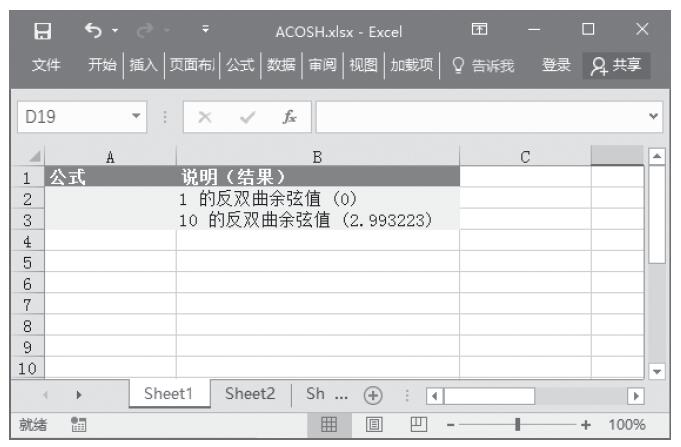
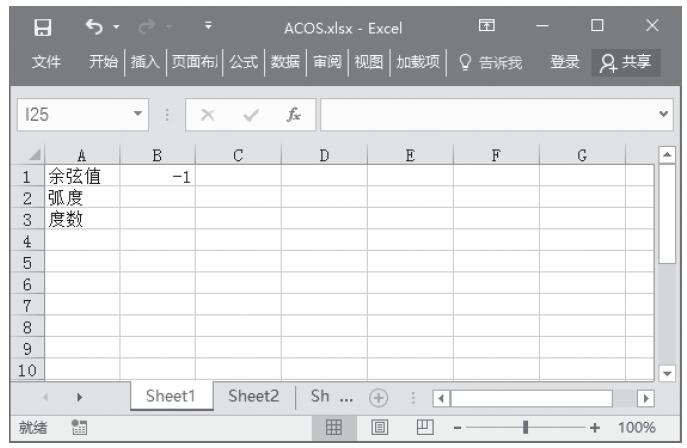
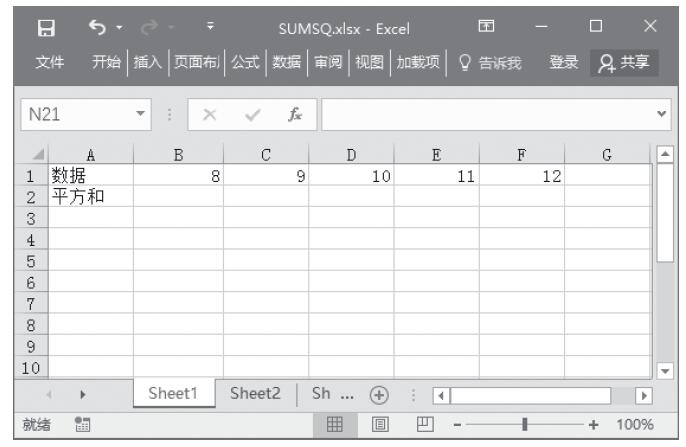
【典型案例】求解各数值的反双曲正切值。本例的原始数据如图13-108所示。
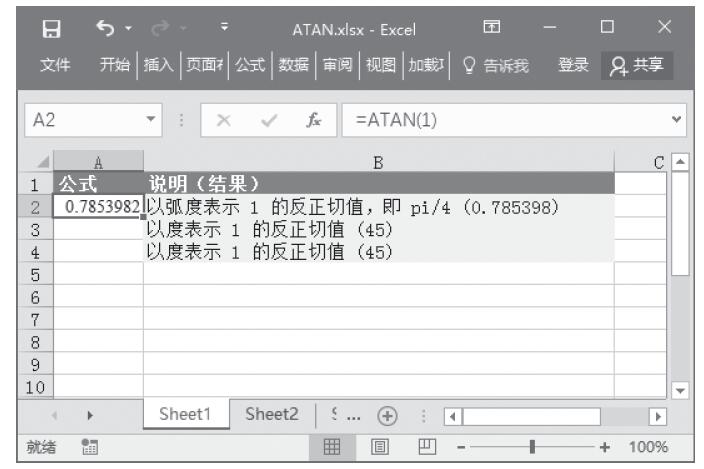
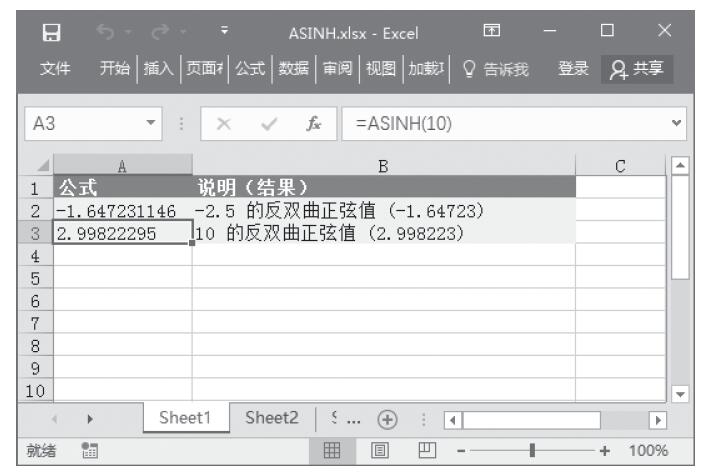
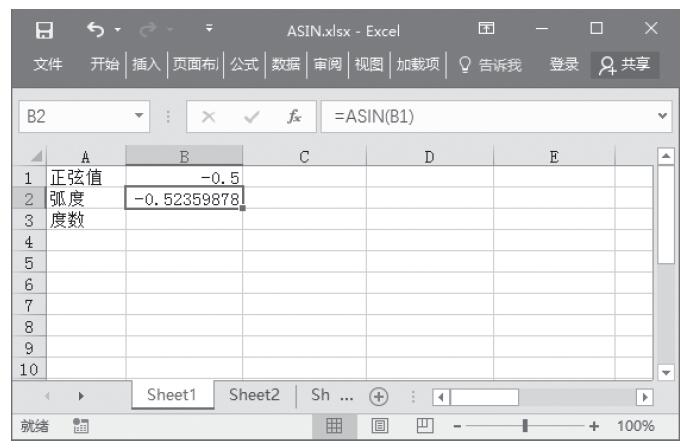
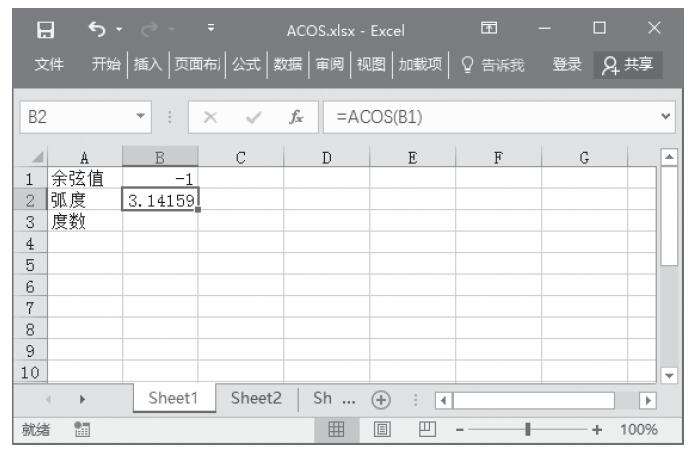
步骤1：在A2单元格中输入公式“=ATANH（0.76159416）”，得到0.76159416的反双曲正切值。
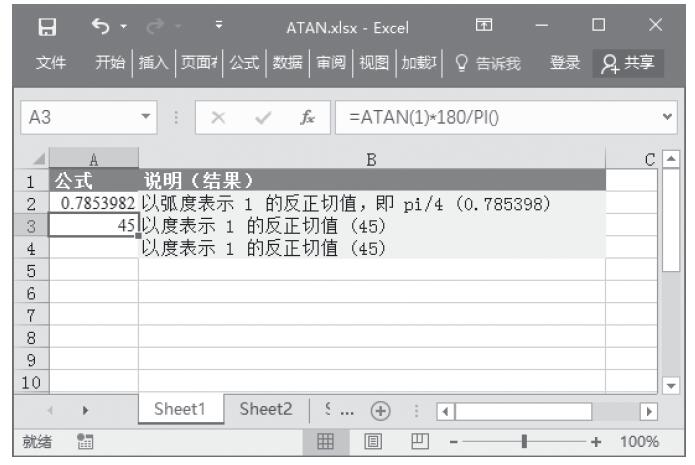
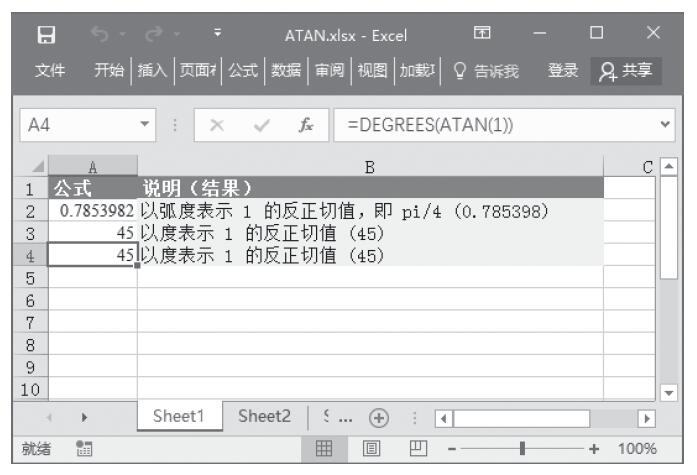
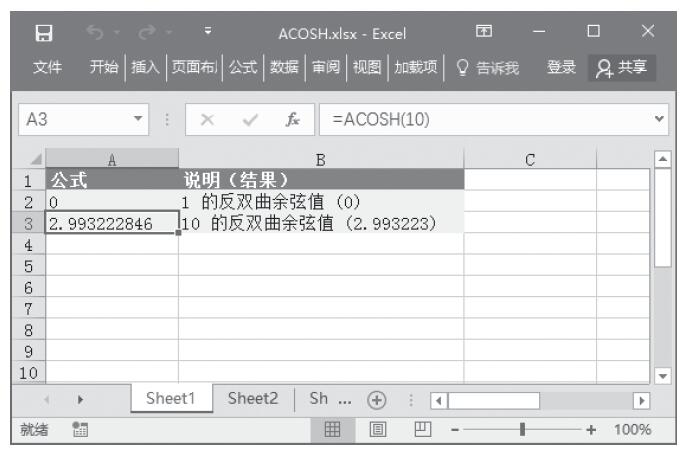
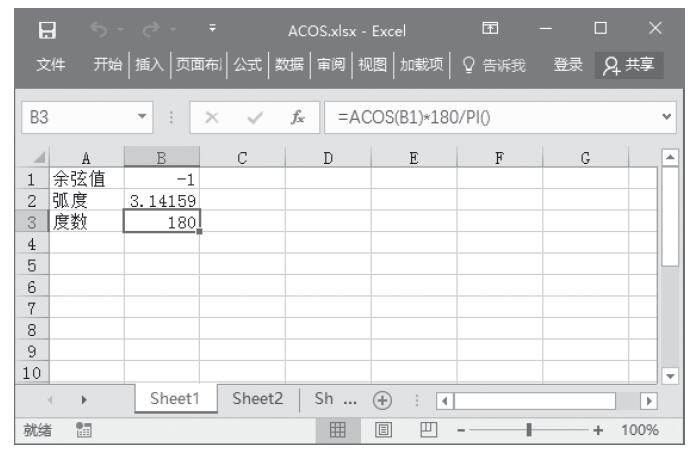
步骤2：在A3单元格中输入公式“=ATANH（-0.1）”，得到-0.1的反双曲正切值，计算结果如图13-109所示。
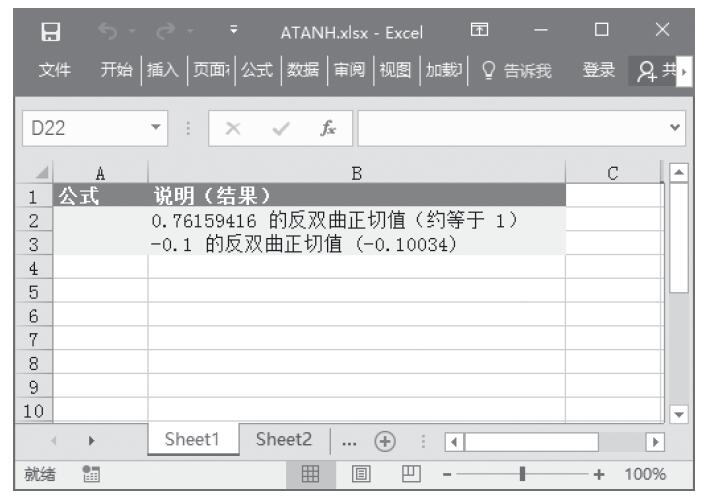
图13-108 原始数据
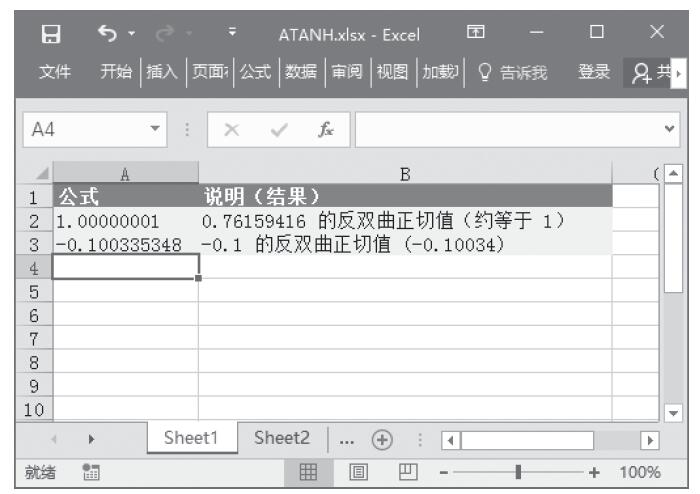
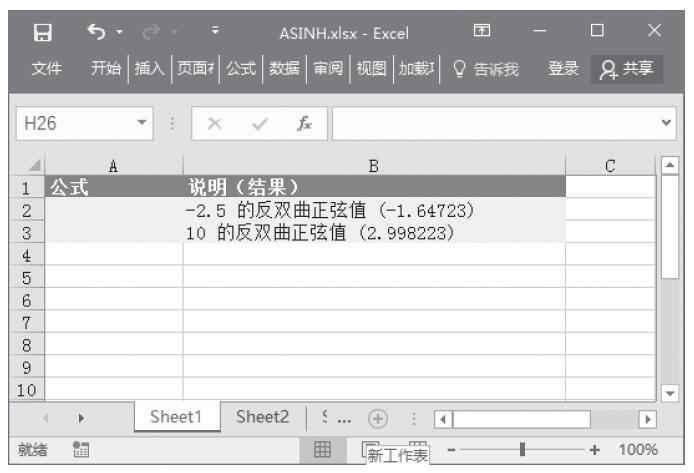
图13-109 计算反双曲正切值
【使用指南】反双曲正切值的双曲正切即为该函数的number参数值，因此ATANH（TANH（number））等于number。
ATAN函数的功能是计算数字的反正切值。反正切值为角度，其正切值即等于参数的值。返回的角度值将以弧度表示，范围为-π/2到π/2。ATAN函数的语法如下：
ATAN(number)
其中参数number为角度的正切值。
【典型案例】求解各数值的反正切值。本例的原始数据如图13-104所示。
步骤1：在A2单元格中输入公式“=ATAN（1）”，得到以弧度表示的1的反正切值，如图13-105所示。
图13-104 原始数据
图13-105 返回以弧度表示的1的反正切值
步骤2：在A3单元格中输入公式“=ATAN（1）*180/PI（）”，得到以弧度表示的1的反正切值，如图13-106所示。
步骤3：在A4单元格中输入公式“=DEGREES（ATAN（1））”，得到以弧度表示的1的反正切值，如图13-107所示。
图13-106 返回反正切值
图13-107 返回反正切值
【使用指南】如果要用度表示反正切值，则将结果再乘以180/PI（）或使用DEGREES函数。
ASINH函数的功能是计算参数的反双曲正弦值。ASINH函数的语法如下：
ASINH(number)
其中参数number为任意实数。
【典型案例】求解各数值的反双曲正弦值。本例的原始数据如图13-102所示。
步骤1：在A2单元格中输入公式“=ASINH（-2.5）”，得到-2.5的反双曲正弦值。
步骤2：在A3单元格中输入公式“=ASINH（10）”，得到10的反双曲正弦值，计算结果如图13-103所示。
图13-102 原始数据
图13-103 计算反双曲正弦值
【使用指南】反双曲正弦值的双曲正弦即等于此函数参数number的值，因此ASINH（SINH（number））等于number参数值。
ASIN函数的功能是计算参数的反正弦值。反正弦值为一个角度，该角度的正弦值即等于此函数的参数number。返回的角度值将以弧度表示，范围为-π/2到π/2。ASIN函数的语法如下：
ASIN(number)
其中参数number为角度的正弦值，必须介于-1到1之间。
【典型案例】已知某角度的正弦值为-0.5，求该角度的弧度和度数。本例的原始数据如图13-98所示。
步骤1：在B2单元格中输入公式“=ASIN（B1）”，求出正弦值为-0.5的角度的弧度数，结果如图13-99所示。
图13-98 原始数据
图13-99 计算弧度结果
步骤2：在B3单元格中输入公式“=ASIN（B1）*180/PI（）”，求出余弦值为-0.5的角度的度数，结果如图13-100所示。
步骤3：在C3单元格中输入公式“=DEGREES（ASIN（-0.5））”，求出余弦值为-0.5的角度的度数，结果如图13-101所示。
图13-100 计算角度结果
图13-101 计算角度结果
【使用指南】如果要用度表示反正弦值，则将结果再乘以180/PI（）或用DEGREES函数表示。
ACOSH函数的功能是计算数字的反双曲余弦值，参数必须大于或等于1。ACOSH函数的语法如下：
ACOSH(number)
其中参数number为大于等于1的实数。
【典型案例】求解各数值的反双曲余弦值。本例的原始数据如图13-96所示。
步骤1：在A2单元格中输入公式“=ACOSH（1）”，得到1的反双曲余弦值。
步骤2：在A3单元格中输入公式“=ACOSH（10）”，得到10的反双曲余弦值，计算结果如图13-97所示。
图13-96 原始数据
图13-97 计算反双曲余弦值
【使用指南】反双曲余弦值的双曲余弦即为该函数的参数number，因此ACOSH（COSH（number））等于number。
ACOS函数的功能是计算数字的反余弦值。反余弦值是角度，它的余弦值为数字。返回的角度值以弧度表示，范围是0到π。ACOS函数的语法如下：
ACOS(number)
其中参数number表示角度的余弦值，必须介于-1到1之间。
【典型案例】已知某角度的余弦值为-1，求该角度的弧度和度数。本例的原始数据如图13-93所示。
步骤1：在B2单元格输入公式“=ACOS（B1）”，求出余弦值为-1的角度的弧度数，结果如图13-94所示。
图13-93 原始数据
图13-94 计算弧度结果
步骤2：在B3单元格输入公式“=ACOS（B1）*180/PI（）”，求出余弦值为-1的角度的度数，结果如图13-95所示。
图13-95 计算角度结果
【使用指南】如果要用度表示反余弦值，则将结果再乘以180/PI（）或用DEGREES函数。
TRUNC函数功能是将数字的小数部分截去，返回整数。其语法如下：
TRUNC(number,num_digits)
其中参数number为需要截尾取整的数字，参数num_digits为用于指定取整精度的数字，参数num_digits的默认值为0。
【典型案例】已知原始数据，对原始数据进行取整运算。本例的原始数据如图13-91所示。
步骤1：在A2单元格中输入公式“=TRUNC（10.9）”，求10.9的整数部分。
步骤2：在A3单元格中输入公式“=TRUNC（-10.9）”，求-10.9的整数部分。
步骤3：在A4单元格中输入公式“=TRUNC（PI（））”，求π的整数部分，计算结果如图13-92所示。
图13-91 原始数据
图13-92 计算结果
【使用指南】TRUNC函数和INT函数类似，都返回整数。TRUNC函数直接去除数字的小数部分，而INT函数则是依照给定数的小数部分的值，将其四舍五入到最接近的整数。INT函数和TRUNC函数在处理负数时有所不同：TRUNC（-4.3）返回-4，而INT（-4.3）返回-5，因为-5是较小的数。
SUMX2MY2函数的功能是计算两数组中对应数值的平方差之和，SUMX2PY2函数用于返回两数组中对应数值的平方和之和。两函数的语法分别如下：
SUMX2MY2(array_x,array_y) SUMX2PY2(array_x,array_y)
其中参数array_x为第一个数组或数值区域，array_y为第二个数组或数值区域。
【典型案例】已知某两列数据，求解这两列数据的平方差之和以及平方和之和。本例的原始数据如图13-89所示。
步骤1：在D1单元格中输入公式“=SUMX2MY2（A2：A6，B2：B6）”，计算数组1和数组2的平方差之和。
步骤2：在D2单元格中输入公式“=SUMX2PY2（A2：A6，B2：B6）”，计算数组1和数组2的平方和之和。计算结果如图13-90所示。
图13-89 原始数据
图13-90 计算结果
【使用指南】SUMX2MY2函数用于计算两数组中对应数值的平方差之和，SUMX2PY2函数用于计算两数组中对应数值的平方和之和，平方和之和在统计计算中经常使用。
SUMXMY2函数的功能是，计算两数组中对应数值之差的平方和。其语法如下：
SUMXMY2(array_x,array_y)
其中参数array_x表示第一个数组或数值区域，参数array_y表示第二个数组或数值区域。
【典型案例】已知某两列数据，求解两组数据的对应差值的平方和。本例的原始数据如图13-87所示。
步骤1：在C2单元格中输入公式“=SUMXMY2（A2：A8，B2：B8）”，计算数组1和数组2的数值之差的平方和。
步骤2：在C3单元格中输入公式“=SUMXMY2（{3，5，7，2，4，6，9}，{8，7，12，3，6，2，5}）”，同样可以计算数组1和数组2的数值之差的平方和。计算结果如图13-88所示，可以看出这两种方法求出的结果相同。
【使用指南】对SUMXMY2函数来说，参数可以是数字、包含数字的名称、数组或引用。如果数组或引用参数包含文本、逻辑值或空白单元格，则这些值将被忽略；但包含零值的单元格将计算在内。如果参数array_x和参数array_y的元素数目不同，SUMXMY2函数将返回错误值“#N/A”。
图13-87 原始数据
图13-88 计算结果
SUMSQ函数的功能是计算参数的平方和。其语法如下：
SUMSQ(number1,number2, ...)
其中参数number、number2、…为1~255个需要求平方和的参数，也可以使用数组或对数组的引用来代替以逗号分隔的参数。
【典型案例】已知某组数据，求这组数据的平方和。本例的原始数据如图13-85所示。
在B2单元格中输入公式“=SUMSQ（B1：F1）”，求以上各数据的平方和，计算结果如图13-86所示。
图13-85 原始数据
图13-86 计算结果
【使用指南】SUMSQ函数主要用来计算数据的平方和。