数学与三角函数应用技巧 – 第4页

Excel 应用RAND函数和RANDBETWEEN函数计算随机实数和随机整数

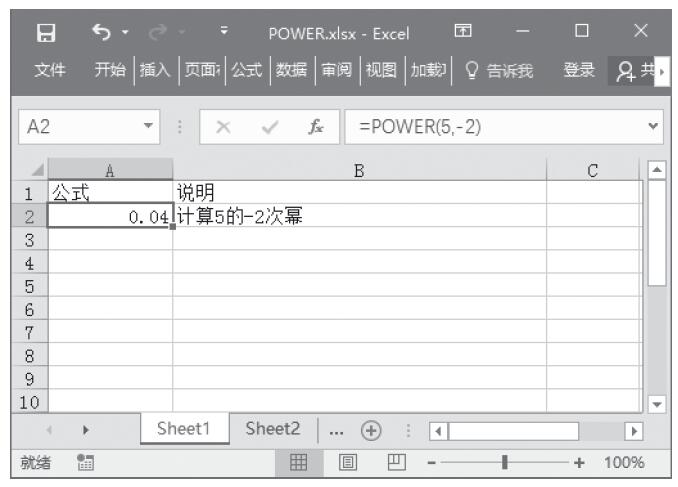
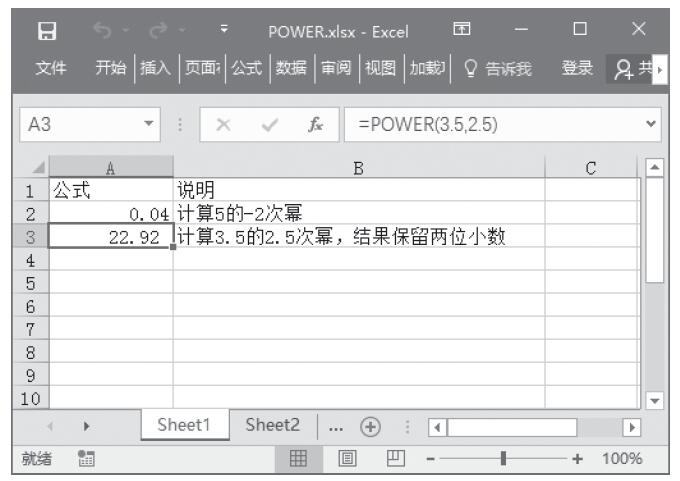
RAND函数和功能是计算大于等于0及小于1的均匀分布的随机实数，每次计算工作表时都将返回一个新的随机实数。RANDBETWEEN函数的功能是，计算位于指定的两个数之间的一个随机整数，每次计算工作表时都将返回一个新的随机整数。两函数的语法如下：

RAND( )
RANDBETWEEN(bottom,top)

其中参数bottom为RANDBETWEEN函数将返回的最小整数，参数top为RANDBETWEEN函数将返回的最大整数。

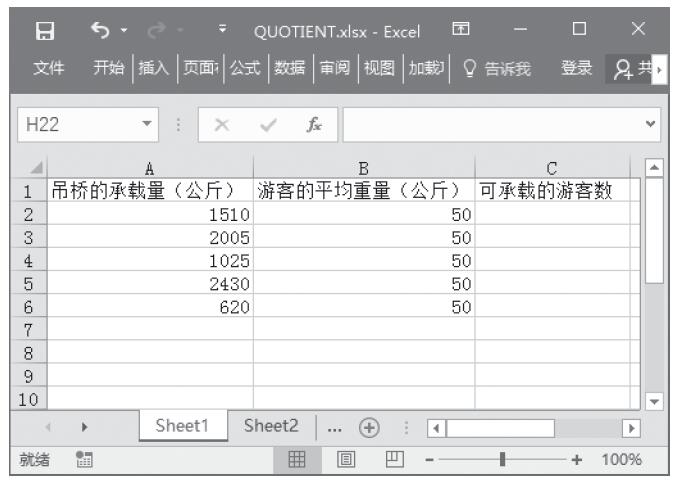
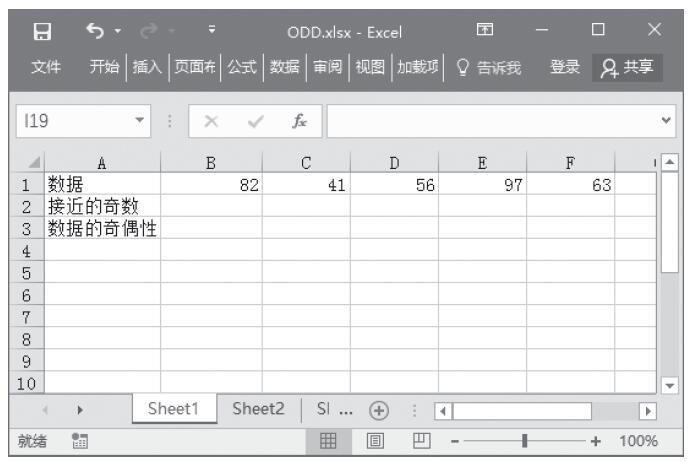
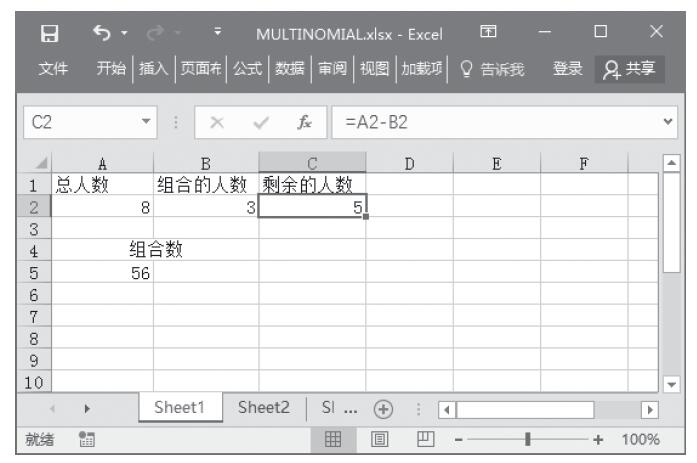
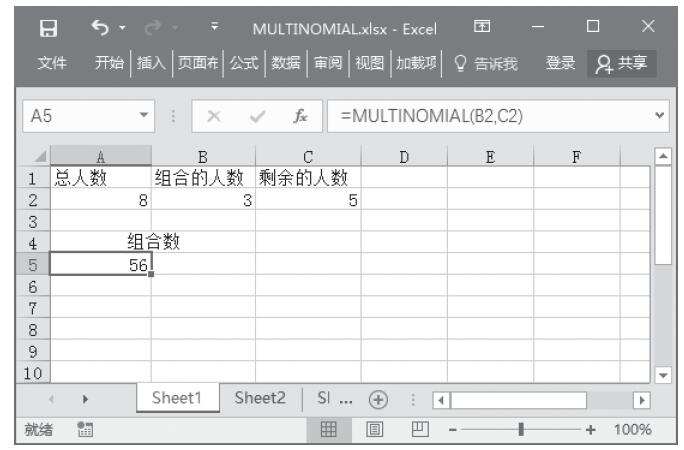
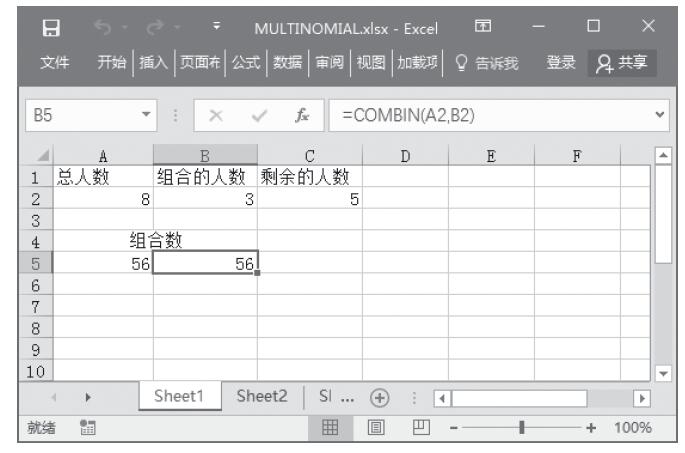
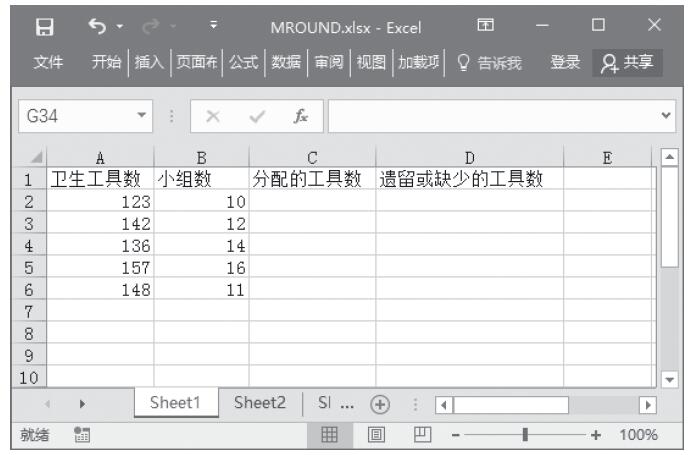
【典型案例】因为这两个函数都是用于返回随机数，所以可以用来模仿一些掷骰子的游戏。本例中要随机返回1~50之间的整数，投掷次数为5次。本例的原始数据如图13-59所示。

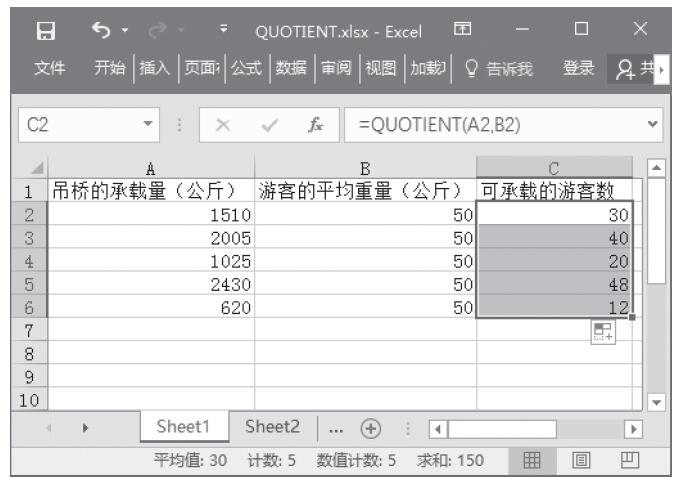
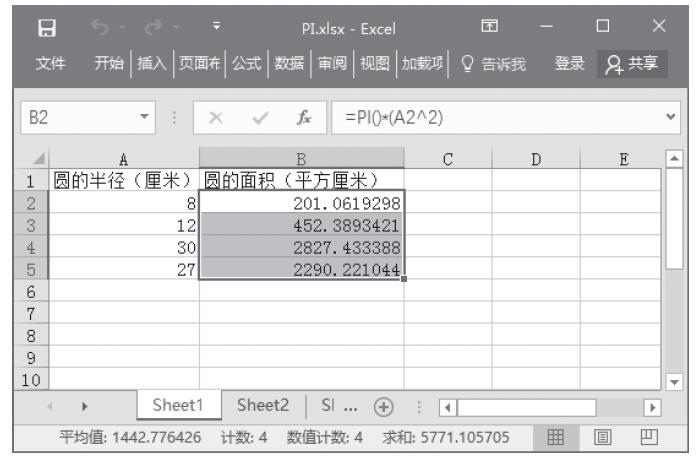
步骤1：在C3单元格中输入公式“=INT（RAND（）*（$B$1-$D$1）+$D$1）”，计算第一次的投掷结果，然后使用自动填充功能来计算其他次数的投掷结果，计算结果如图13-60所示。

图13-59　原始数据

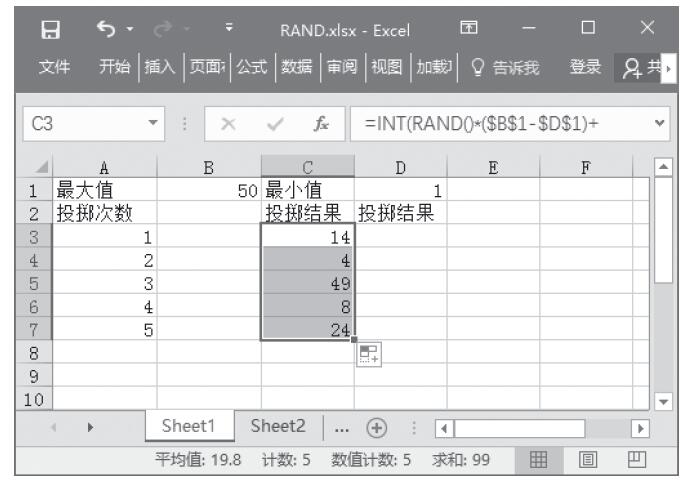
图13-60　计算投掷结果

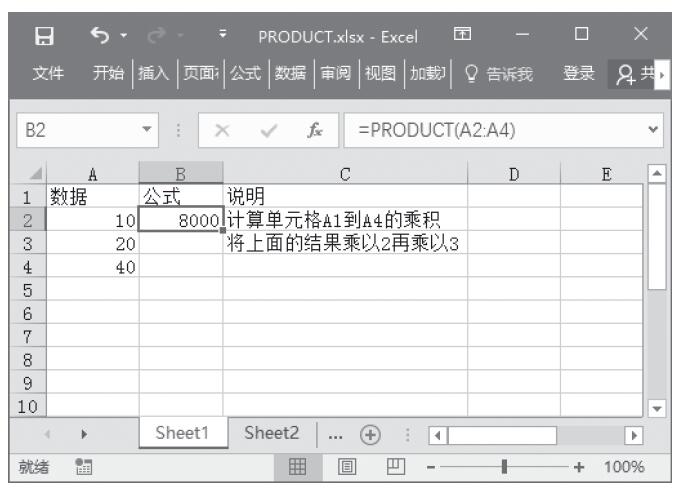
步骤2：在D3单元格中输入公式“=INT（RANDBETWEEN（$D$1，$B$1））”，计算第一次的投掷结果，然后使用自动填充功能来计算其他次数的投掷结果，计算结果如图13-61所示。

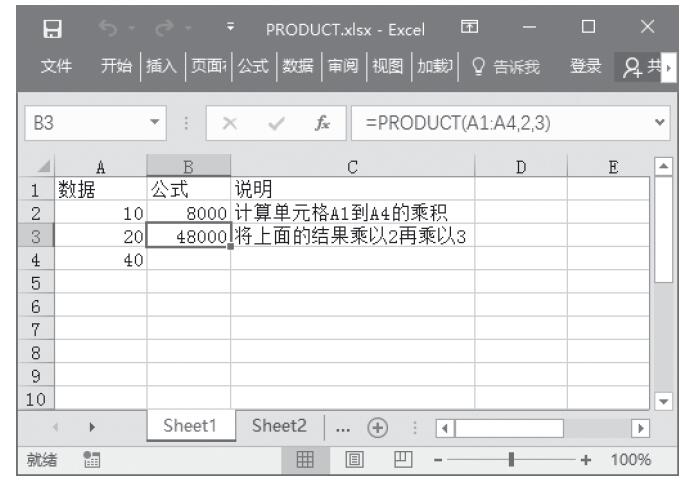
步骤3：重新查看投掷结果。按F9键可以查看重新求解的随机结果，计算结果如图13-62所示。

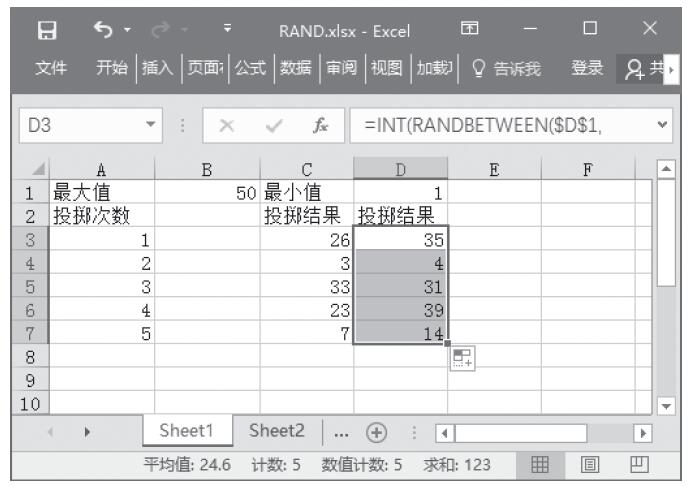
图13-61　计算投掷结果

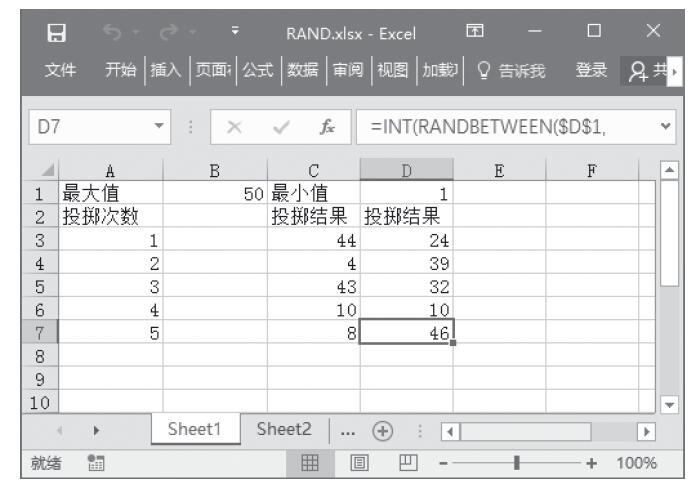
图13-62　重新查看投掷结果

【使用指南】对RAND函数来说：如果要生成a与b之间的随机实数，必须使用“RAND（）*（b-a）+a”。如果要使用RAND函数生成一随机数，并且使之不随单元格计算而改变，可以在编辑栏中输入“=RAND（）”，保持编辑状态，然后按F9键，将公式永久性地改为随机数。

Excel 应用QUOTIENT函数计算商的整数部分

QUOTIENT函数的功能是计算商的整数部分，该函数可用于舍掉商的小数部分。其语法如下：

QUOTIENT(numerator,denominator)

其中参数number为被除数，参数denominator为除数。

【典型案例】某旅游景点准备架设几座吊桥，为了游客的安全，每座吊桥都有对应的承重量，以限制上桥人数。假设游客的平均体重为50kg，求解每座吊桥能承载的游客人数。本例的原始数据如图13-57所示。

在C2单元格中输入公式“=QUOTIENT（A2，B2）”，计算第一个吊桥所能承载的游客数，然后使用自动填充功能来计算其他吊桥所能承载的游客数，计算结果如图13-58所示。

图13-57　原始数据

图13-58　计算可承载的游客数

【使用指南】对QUOTIENT函数来说，如果任一参数为非数值型，则QUOTIENT函数返回错误值“#VALUE！”。

Excel 应用PRODUCT函数计算指定数值的乘积

PRODUCT函数的功能是将所有以参数形式给出的数字进行相乘，并返回乘积值。其语法如下：

PRODUCT(number1,number2,...)

其中参数number1、number2等是要相乘的1到255个数字。

【典型案例】PRODUCT函数就是用来计算不同数据的乘积。

步骤1：在B2单元格中输入公式“=PRODUCT（A2：A4）”，计算单元格A2到A4的乘积，计算结果如图13-55所示。

图13-55　计算单元格A2到A4的乘积

步骤2：在B3单元格中输入公式“=PRODUCT（A2：A4，2，3）”，计算单元格A2到A4的乘积再乘以2再乘以3，计算结果如图13-56所示。

【使用指南】PRODUCT函数主要用于计算各种情况下数字的乘积，对PRODUCT函数来说：当参数为数字、逻辑值或数字的文字型表达式时可以被计算；当参数为错误值或是不能转换为数字的文字时，将导致错误。如果参数为数组或引用，只有其中的数字将被计算。数组或引用中的空白单元格、逻辑值、文本或错误值将被忽略。

图13-56　计算结果

Excel 应用POWER函数计算给定数字的乘幂

POWER函数的功能是，计算给定数字的乘幂。其语法如下：

POWER(number,power)

其中参数number为底数，可以为任意实数；参数power为指数，底数按该指数次幂乘方。

【典型案例】POWER函数就是用来计算不同数据的乘幂。

步骤1：在A2单元格中输入公式“=POWER（5，-2）”，计算5的-2次幂，计算结果如图13-53所示。

步骤2：在A3单元格中输入公式“=POWER（3.5，2.5）”，计算3.5的2.5次幂，并将结果保留两位小数，计算结果如图13-54所示。

图13-53　计算5的-2次幂

图13-54　计算3.5的2.5次幂

【使用指南】POWER函数主要用来计算不同数据的乘幂。可以用“^”运算符代替函数POWER函数来表示对底数乘方的幂次，例如7^2的结果等同于公式“=POWER（7，2）”的结果。

Excel 应用PI函数和SQRTPI函数计算π值和返回某数与π的乘积的平方根

PI函数的功能是返回数字3.14159265358979，即数学常量π，精确到小数点后14位。SQRTPI函数的功能是计算某数与π的乘积的平方根。两函数的语法如下：

PI( )
SQRTPI(number)

其中参数number为用来与π相乘的数。

【典型案例】已知圆的半径，求圆的面积。本例的原始数据如图13-51所示。

在B2单元格中输入公式“=PI（）*（A2^2）”，计算第一个圆的面积，然后使用自动填充功能来计算其他圆的面积，计算结果如图13-52所示。

图13-51　原始数据

图13-52　计算圆的面积

【使用指南】PI函数的作用就是用来返回常量π，可以参与于常量π相关的计算。对SQRTPI函数来说，如果参数number<0，则SQRTPI函数返回错误值“#NUM！”。

Excel 应用ODD函数计算对指定数值向上舍入后的奇数

ODD函数的功能是计算对指定数值进行向上舍入后的奇数。其语法如下：

ODD(number)

其中参数number是要进行四舍五入的数值。

【典型案例】使用ODD函数也可以来判断数字的奇偶性。已知某行数据，判断这些数据的奇偶性。本例的原始数据如图13-48所示。

步骤1：在B2单元格中输入公式“=ODD（B1）”，计算和第一个数据向上的最接近的奇数。然后使用自动填充功能来计算其他数据向上最接近的奇数，计算结果如图13-49所示。

图13-48　原始数据

图13-49　计算接近的奇数

步骤2：判断数据的奇偶性。在B3单元格中输入公式“=IF（B2=B1，”奇数”，”偶数”）”，判断第一个数据的奇偶性，然后使用自动填充功能来判断其他数据的奇偶性，计算结果如图13-50所示。

图13-50　判断数据的奇偶性

【使用指南】对ODD函数来说，如果参数number为非数值参数，则ODD函数将返回错误值“#VALUE！”。如果参数number恰好是奇数，则不必进行任何舍入处理。无论数字符号如何，都按远离0的方向向上舍入。

Excel 应用MULTINOMIAL函数计算一组数字的多项式

MULTINOMIAL函数的功能是计算参数和的阶乘与各参数阶乘乘积的比值。其语法如下：

MULTINOMIAL(number1,number2,...)

其中参数number1、number2等是用于进行函数MULTINOMIAL运算的1到255个值。

【典型案例】某车间小组共有8人，现从8人中任选3人进行组合，以小组为单位进行值班，求解所有的组合数。本例的原始数据如图13-44所示。

步骤1：在C2单元格中输入公式“=A2-B2”，计算剩余的人数，计算结果如图13-45所示。

图13-44　原始数据

图13-45　计算剩余的人数

步骤2：在A5单元格中输入公式“=MULTINOMIAL（B2，C2）”，计算组合数，结果如图13-46所示。

步骤3：在B5单元格中输入公式“=COMBIN（A2，B2）”，使用COMBIN函数来再次计算组合数，以验证结果，计算结果如图13-47所示。

图13-46　计算组合数

图13-47　计算组合数

【使用指南】对MULTINOMIAL函数来说，如果有些参数为非数值型，则MULTINOMIAL函数将返回错误值“#VALUE！”。如果有小于0的参数，则MULTINOMIAL函数返回错误值“#NUM！”。

Excel 应用MROUND函数计算按指定基数舍入后的数值

MROUND函数的功能是计算参数按指定基数舍入后的数值。其语法如下：

MROUND(number,multiple)

其中参数number是要进行四舍五入的数值，参数multiple是要对数值number进行四舍五入的基数。

【典型案例】某学校要进行卫生大扫除，需要分配卫生工具给不同的小组，只有小组全部获得卫生工具才能开始大扫除，因此要计算分配多余或缺少的工具数。本例的原始数据如图13-41所示。

步骤1：计算分配的工具数。在C2单元格中输入公式“=MROUND（A2，B2）”，按Enter键，计算第一种卫生工具的分配数，然后使用自动填充功能来计算其他卫生工具的分配数，计算结果如图13-42所示。

步骤2：计算剩余或缺少的工具数。在D2单元格中输入公式“=ABS（A2-C2）”，计算第一种卫生工具所剩余或缺少的数目，然后使用自动填充功能来计算其他卫生工具的剩余或缺少的数目，计算结果如图13-43所示。

图13-41　原始数据

图13-42　计算分配的工具数

图13-43　计算遗留或缺少的工具数

【使用指南】在MROUND函数中，如果参数number除以基数的余数大于或等于基数的一半，则MROUND函数将向远离零的方向舍入。如果该函数不可用，并返回错误值“#NAME？”，那么须安装并加载“分析工具库”来加载宏。

Excel 应用MOD函数计算两数相除的余数

MOD函数功能是计算两数相除的余数。结果的正负号与除数相同。其语法如下：

MOD(number,divisor)

其中参数number为被除数，divisor为除数。

【典型案例】使用MOD函数来判断数字的奇偶性，本例的原始数据如图13-38所示。

步骤1：计算数据除以2的余数。在B2单元格中输入公式“=MOD（B1，2）”，按Enter键，计算第一个数据除以2后的余数，然后使用自动填充功能来计算其他数据除以2的余数，计算结果如图13-39所示。

图13-38　原始数据

图13-39　计算余数

步骤2：在B3单元格中输入公式“=IF（B2=1，”奇数”，”偶数”）”，按Enter键，判断第一个数据的奇偶性，然后使用自动填充功能来计算其他数据的奇偶性，计算结果如图13-40所示。

图13-40　判断奇偶性

【使用指南】在MOD函数中，如果参数divisor为零，MOD函数将返回错误值“#DIV/0！”。MOD函数可以借用函数INT来表示：MOD（n，d）=n-d*INT（n/d）。

Excel 应用MINVERSE函数和MMULT函数计算逆矩阵和矩阵乘积

MINVERSE函数的功能是计算数组中存储的矩阵的逆矩阵。MMULT函数的功能是，计算两个数组的矩阵乘积。结果矩阵的行数与参数array1的行数相同，矩阵的列数与参数array2的列数相同。两函数的语法分别如下：

MINVERSE(array)
MMULT(array1,array2)

其中参数array是行数和列数相等的数值数组。参数array1、array2是要进行矩阵乘法运算的两个数组，可以是单元格区域、数组常量或引用。

【背景知识】在MINVERSE函数中，提到了一个概念逆矩阵。图13-33所示的是计算二阶方阵逆矩阵的示例。假设A1：B2中包含以字母a、b、c和d表示的四个任意的数，则该表表示矩阵A1：B2的逆矩阵。

图13-33　矩阵A1：B2的逆矩阵

【典型案例】使用MINVERSE函数和MMULT函数，求下面的三元一次方程组的解。

本例的原始数据如图13-34所示。

步骤1：求解系数矩阵的逆矩阵。选中A13~C15单元格区域，在编辑栏中输入公式“=MINVERSE（A7：C9）”，然后按组合键“Ctrl+Shift+Enter”，计算出系数矩阵的逆矩阵，结果如图13-35所示。

图13-34　原始数据

图13-35　计算系数矩阵的逆矩阵

步骤2：求三元一次方程组的数值矩阵。选中F13~F15单元格区域，在编辑栏中输入公式“=MMULT（A13：C15，E7：E9）”，然后按组合键“Ctrl+Shift+Enter”，计算出方程组的数值矩阵，即方程组的解，结果如图13-36所示。

步骤3：检查方程组的解是否正确。在G7单元格中输入公式“=A7*$F$13+B7*$F$14+C7*$F$15=E7”，用来检查方程组的解是否满足第一个方程，然后使用自动填充功能来检查下面的两个方程，检查结果如图13-37所示。

图13-36　求三元一次方程组的数值矩阵

图13-37　检查结果

【使用指南】与求行列式的值一样，求解逆矩阵常被用于求解多元联立方程组。所以将MINVERSE函数和MMULT函数合在一起，求解一个方程组。

在MINVERSE函数中，参数array可以是单元格区域，或单元格区域和数组常量的名称。如果参数array中的单元格为空、包含文字或行和列的数目不相等，则函数MINVERSE将返回错误值“#VALUE！”。对于一些不能求逆的矩阵，MINVERSE函数将返回错误值“#NUM！”。不能求逆的矩阵的行列式值为零。

在MMULT函数中，参数array1的列数与参数array2的行数必须相同，而且两个数组中都只能包含数值。如果参数array1和参数array2中的单元格为空、包含文字或行和列的数目不相等，MMULT函数将返回错误值“#VALUE！”。