数学与三角函数应用技巧 – 第5页

Excel 应用MDETERM函数计算矩阵行列式的值

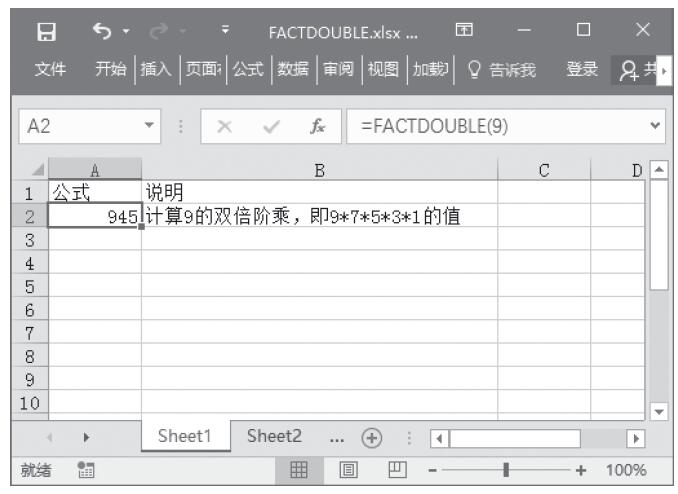
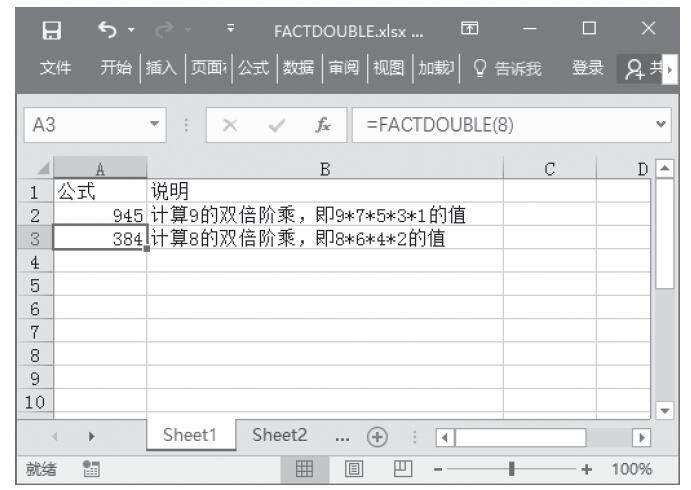
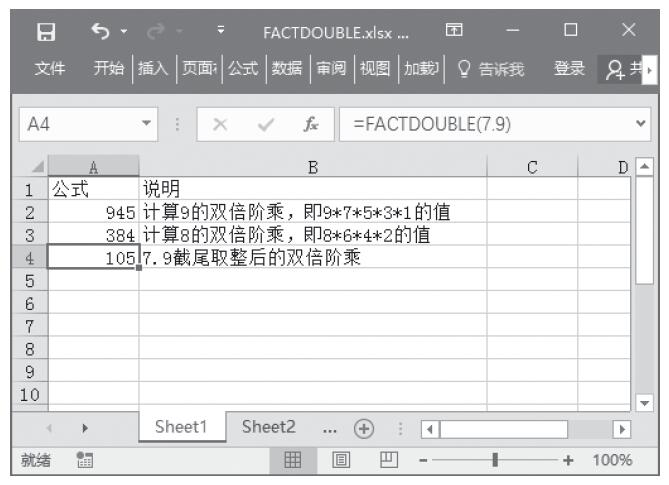
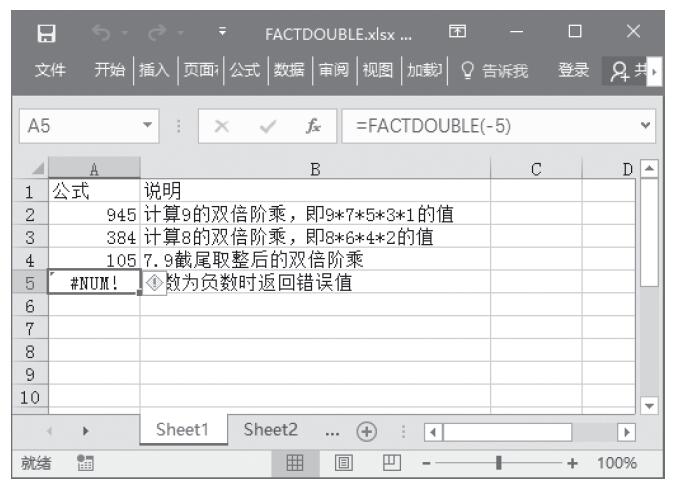
MDETERM函数的功能是计算一个数组的矩阵行列式的值。其语法如下：

MDETERM(array)

其中参数array为行数和列数相等的数值数组。

【背景知识】矩阵行列式的值是由数组中的各元素计算而来的。对一个三行、三列的数组A1：C3，其行列式的值定义如下：

MDETERM（A1：C3）=A1*（B2*C3-B3*C2）+A2*（B3*C1-B1*C3）+A3*（B1*C2-B2*C1）

【典型案例】已知某矩阵，求解矩阵的行列式，并根据行列式判断矩阵是否可逆。本例的原始数据如图13-30所示。

步骤1：在B6单元格中输入公式“=MDETERM（A1：D4）”，按Enter键，计算该矩阵行列式，计算结果如图13-31所示。

图13-30　原始数据

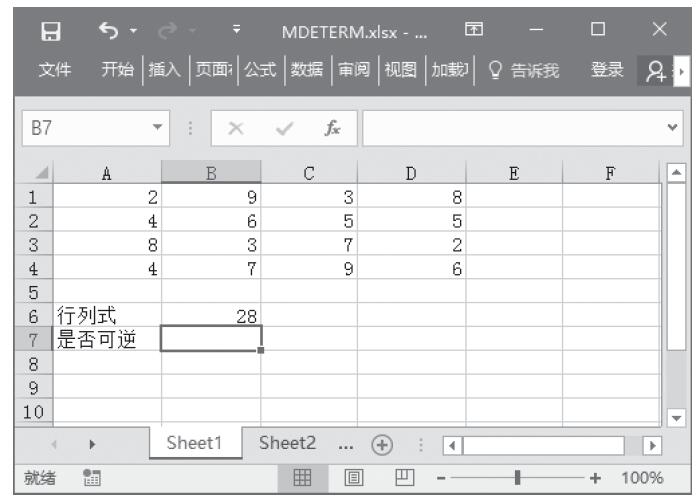
图13-31　计算行列式

步骤2：在B7单元格中输入公式“=IF（MDETERM（A1：D4）<>0，”可逆”，”不可逆”）”，按Enter键，判断矩阵是否可逆，计算结果如图13-32所示。

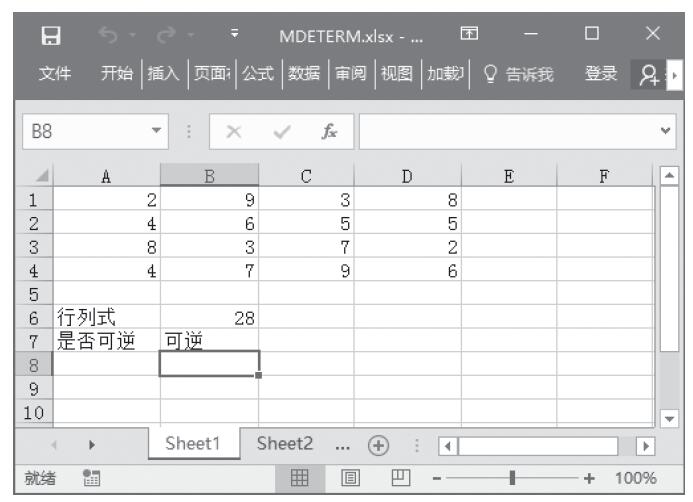
图13-32　判断矩阵是否可逆

【使用指南】矩阵的行列式值常被用来求解多元联立方程。MDETERM函数的精确度可达16位有效数字，因此运算结果因位数的取舍可能会导致某些微小误差。在MDETERM函数中，参数array可以是单元格区域，或是区域或数组常量的名称。如果参数array中的单元格为空、包含文字或行和列的数目不相等，MDETERM函数将返回错误值“#VALUE！”。

Excel 应用LN函数、LOG函数和LOG10函数计算对数

LN函数的功能是计算一个数的自然对数，自然对数以常数项e（2.71828182845904）为底。LOG函数的功能是，计算按所指定的底数返回一个数的对数。LOG10函数的功能是计算以10为底的对数。三个函数的语法如下：

LN(number)
LOG(number,base)
LOG10(number)

其中参数number为用于计算对数的正实数，base为对数的底数。如果省略底数，则假定其值为10。

【典型案例】已知有4家上市企业，分别是AC钢铁、DF制药、ER玩具和QI服装，从2007年9月到2008年2月的股票指数数据，投资分析人员需要计算股票的月收益率，以连续复利计，原始的指数数据如图13-28所示。

图13-28　原始数据

在F3单元格中输入公式“=LN（B3/B2）”，计算AC钢铁企业在2007年10月份的股票收益率，然后使用纵向自动填充功能来计算其他日期的收益率，使用横向自动填充功能来计算其他企业的收益率，结果如图13-29所示。

图13-29　计算结果

【使用指南】LN函数是EXP函数的反函数。在LOG函数中，如果省略参数base，就假定其值为10。

Excel 应用INT函数将数字向下舍入到最接近的整数

INT函数的功能是将数字向下舍入到最接近的整数。其语法如下：

INT(number)

其中参数number为需要进行向下舍入取整的实数。

【典型案例】某旅游公司新进了几辆旅游车，每辆车的载重不一样，所能乘载的客人数也不一样。现在假设每个游客的重量为50kg，计算每辆车能乘载的游客数。本例的原始数据如图13-26所示。

在C2单元格中输入公式“=INT（A2/B2）”，计算出第一辆车所能乘载的游客数，然后使用自动填充功能来计算其他车辆所能乘载的游客数，结果如图13-27所示。

图13-26　原始数据

图13-27　计算结果

【使用指南】在INT函数中，如果参数为非数值型，INT函数将返回错误值“#VALUE！”。

Excel 应用GCD函数和LCM函数计算整数的最大公约数和最小公倍数

GCD函数的功能是返回两个或多个整数的最大公约数，最大公约数是能分别将参数number1和number2除尽的最大整数。LCM函数的功能是，返回整数的最小公倍数。最小公倍数是所有整数参数number1、number2等的最小正整数倍数。两函数的语法分别如下：

GCD(number1,number2,…)
LCM(number1,number2, …)

其中参数number1，number2，…为1到255个参数。如果参数不是整数，则截尾取整。

【典型案例】给出两个参数数值，求解两参数的最大公约数和最小公倍数。本例的原始数据如图13-24所示。

在B2单元格中输入公式“=GCD（B1：C1）”，计算两参数的最大公约数，结果为“24”。在B3单元格中输入公式“=LCM（B1：C1）”，计算两参数的最小公倍数，结果为“144”。如图13-25所示。

图13-24　原始数据

图13-25　计算结果

【使用指南】LCM函数可以用于将分母不同的分数相加。对两函数来说，如果参数为非数值型，则两函数都将返回错误值“#VALUE！”。如果参数小于零，则两函数都将返回错误值“#NUM！”。

Excel 应用FLOOR函数计算向下舍入最接近的倍数

FLOOR函数的功能是将某数值向下舍入（向零的方向）到最接近的倍数。其语法如下：

FLOOR(number,significance)

其中参数number为所要四舍五入的数值，参数significance为用以进行舍入计算的倍数。

【典型案例】某学校的会计部门为了统计方便，对所收的书本费结果取两位小数，同时统计单位为“千元”。本例的原始数据如图13-22所示。

在E2单元格中输入公式“=FLOOR（D2/1000，0.01）”，计算出计算机班支付的会计数据，然后使用自动填充功能来计算其他班级的要支付的会计数据，结果如图13-23所示。

图13-22　原始数据

图13-23　计算结果

【使用指南】在FLOOR函数中，如果任一参数为非数值型，则FLOOR函数将返回错误值“#VALUE！”。如果参数number和参数significance的符号相反，则FLOOR函数将返回错误值“#NUM！”。不论参数number的正负号如何，舍入时参数的绝对值都将减小。如果参数number已经为参数significance的倍数，则不需要进行任何舍入。

Excel 应用FACTDOUBLE函数计算数字的双倍阶乘

FACTDOUBLE函数的功能是计算数字的双倍阶乘。其语法如下：

FACTDOUBLE(number)

其中参数number为要计算其双倍阶乘的数值。如果number不是整数，将截尾取整。

【背景知识】参数的奇偶性不同，双倍阶乘的计算方法就不一样。如果参数number为偶数，计算公式为n！！=n（n-2）（n-4）…（4）（2）。如果参数number为奇数，计算公式为n！！=n（n-2）（n-4）…（3）（1）。

【典型案例】FACTDOUBLE函数主要用来计算不同参数的阶乘数值。

步骤1：新建一个工作簿并保存为“FACTDOUBLE.xlsx”。在A2单元格中输入公式“=FACTDOUBLE（9）”，计算9的双倍阶乘，结果如图13-18所示。

步骤2：在A3单元格中输入公式“=FACTDOUBLE（8）”，计算8的双倍阶乘，结果如图13-19所示。

图13-18　计算9的双倍阶乘

图13-19　计算8的双倍阶乘

步骤3：在A4单元格中输入公式“=FACTDOUBLE（7.9）”，截尾取整后计算7的双倍阶乘，结果如图13-20所示。

步骤4：在A5单元格中输入公式“=FACTDOUBLE（-5）”，按Enter键，可以看到返回结果为“#NUM！”，结果如图13-21所示。

图13-20　截尾取整后计算7的双倍阶乘

图13-21　参数为负数时返回的结果

【使用指南】在用FACTDOUBLE函数计算双倍阶乘时，如果参数number为非数值型，FACTDOUBLE函数将返回错误值“#VALUE！”。如果参数number为负值，FACTDOUBLE函数将返回错误值“#NUM！”。

Excel 应用FACT函数计算某数的阶乘

FACT函数的功能是计算某正数的阶乘。其语法如下：

FACT(number)

其中参数number为要计算其阶乘的数值。

【背景知识】一个数的阶乘等于1×2×3×…

【典型案例】FACT函数主要用来计算不同参数的阶乘数值。

步骤1：新建一个工作簿并保存为“FACT.xlsx”。在A2单元格中输入公式“=FACT（5）”，计算5的阶乘，结果如图13-14所示。

步骤2：在A3单元格中输入公式“=FACT（8.6）”，计算8的阶乘，结果如图13-15所示。

图13-14　计算5的阶乘

图13-15　计算8.6截尾取整后的阶乘

步骤3：在A4单元格中输入公式“=FACT（-6）”，按Enter键，可以看到返回结果为“#NUM！”，结果如图13-16所示。

步骤4：在A5单元格中输入公式“=FACT（171）”，按Enter键，可以看到返回结果为“#NUM！”，结果如图13-17所示。

图13-16　参数为负数时返回的结果

图13-17　参数超过170后返回的结果

【使用指南】阶乘主要用于排列和组合的计算。在用FACT函数计算阶乘时，如果参数number不是整数，将截尾取整进行计算。如果参数为负数，将会返回错误值“#NUM！”。因为计算阶乘时，参数越大，结果越大，Excel 2007只能支持170以下的正数阶乘的计算，超过170后，FACT函数将会返回错误值“#NUM！”。

Excel 应用EXP函数计算e的n次幂

EXP函数的功能是计算e的n次幂。EXP函数的语法如下：

EXP(number)

其中参数number为应用于底数e的指数。

【背景知识】常数e等于2.71828182845904，是自然对数的底数。

【典型案例】已知某函数表达式y=ex，现求解x的取值在-5~5之间的函数曲线。本例的原始数据如图13-10所示。

步骤1：在B2单元格中输入公式“=EXP（B1）”，求出y=e-5的值，然后使用自动填充功能来计算函数的其他值，计算结果如图13-11所示。

图13-10　原始数据

图13-11　计算函数值

步骤2：单击功能区的“插入”选项卡的“图表”组中的“散点图”按钮，在弹出的菜单中选择“带平滑线的散点图”，如图13-12所示。

步骤3：系统自动生成曲线，如图13-13所示。

【使用指南】用EXP函数可以计算不同参数的指数数值。e=2.71828182…是微积分中的两个常用极限之一，它有一些特殊的性质，使得在数学、物理等学科中有广泛应用。在使用EXP函数时，如果要计算以其他常数为底的幂，须使用指数操作符（^）。EXP函数是计算自然对数的LN函数的反函数。

图13-12　选择“带平滑线的散点图”

图13-13　生成曲线

Excel 应用EVEN函数计算取整后最接近的偶数

EVEN函数的功能是计算沿数值绝对值增大的方向，进行取整后最接近的偶数。EVEN函数的语法如下：

EVEN(number)

其中参数number是要进行四舍五入的数值。

【典型案例】某次班级小考中，为了方便统计成绩，将平均分都按照偶数统计。本例的原始数据如图13-8所示。

在C2单元格中输入公式“=EVEN（A2/B2）”，按Enter键，计算出第一个同学的平均分，然后使用自动填充功能来计算其他同学的平均分，结果如图13-9所示。

【使用指南】使用EVEN函数可以处理那些成对出现的对象。例如，一个包装箱一行可以装一宗或两宗货物，只有当这些货物的宗数向上取整到最近的偶数，与包装箱的容量相匹配时，包装箱才会装满。在EVEN函数中，如果参数number为非数值参数，则EVEN函数将返回错误值“#VALUE！”。不论参数number的正负号如何，函数都向远离零的方向舍入，如果参数number恰好是偶数，则无需进行任何舍入处理。

图13-8　原始数据

图13-9　计算平均分

Excel 应用COMBIN函数计算给定数目对象的组合数

COMBIN函数的功能是计算从给定数目的对象集合中，提取若干对象的组合数。COMBIN函数的语法如下：

COMBIN(number,number_chosen)

其中参数number表示项目的数量，参数number_chosen表示每一个组合中项目的数量。

【典型案例】某工厂车间有5个人，分别是张静、李平、苏刚、王辉和吕丽，现在要从这5人中抽出4人进行技能比赛，计算可以组成的组合数。本例的原始数据如图13-6所示。

在C2单元格中输入公式“=COMBIN（A2，B2）”，按Enter键，计算出可组合数，可以看到返回结果为“5”，如图13-7所示。

图13-6　原始数据

图13-7　检验组合数

【使用指南】使用COMBIN函数可以确定一组对象所有可能的组合数。在COMBIN函数中的数字参数将截尾取整。如果参数为非数值型，则COMBIN函数将返回错误值“#VALUE！”。如果参数number<0、参数number_chosen<0或参数number<参数number_chosen，则COMBIN函数将返回错误值“#NUM！”。