Excel中的统计函数主要用于对数据区域进行各种分类统计与分析。统计函数包括了许多统计学领域的函数，具体包括平均值函数、Beta分布函数、概率函数、单元格数量计算函数、指数与对数函数、最大值与最小值函数、标准偏差函数、方差函数、正态累积分布函数、数据集相关函数、Pearson乘积矩函数、t分布函数等。本章将通过实例介绍统计函数的基本语法、参数用法以及在实际中的应用。
某公司于月初发放了上月份员工奖金，包括销售奖励与全勤奖励两种，现在需要对奖金发放人数进行统计。有的员工不只发放了销售奖金，还发放了全勤奖，所以统计时应该考虑到重复出现的员工姓名。下面介绍具体的实现过程。基础数据如图16-172所示。
步骤1：单击G2单元格，按F2键，输入公式“=SUM（1/COUNTIF（A3：A14，A3：A14））”。
说明：以上公式先利用COUNTIF函数返回单元格区域内某记录出现的次数的数组，取倒数，然后求和。如果姓名不重复出现则得到1，如果重复出现2次则得到1/2，求和之后仍然是1，这样可以实现不重复统计。
步骤2：输入完成后按“Ctrl+Shift+Enter”键，以数组公式的形式完成输入，得到结果如图16-173所示。
图16-172 基础数据
图16-173 计算结果
经过以上操作，即实现了奖金发放人数的统计。
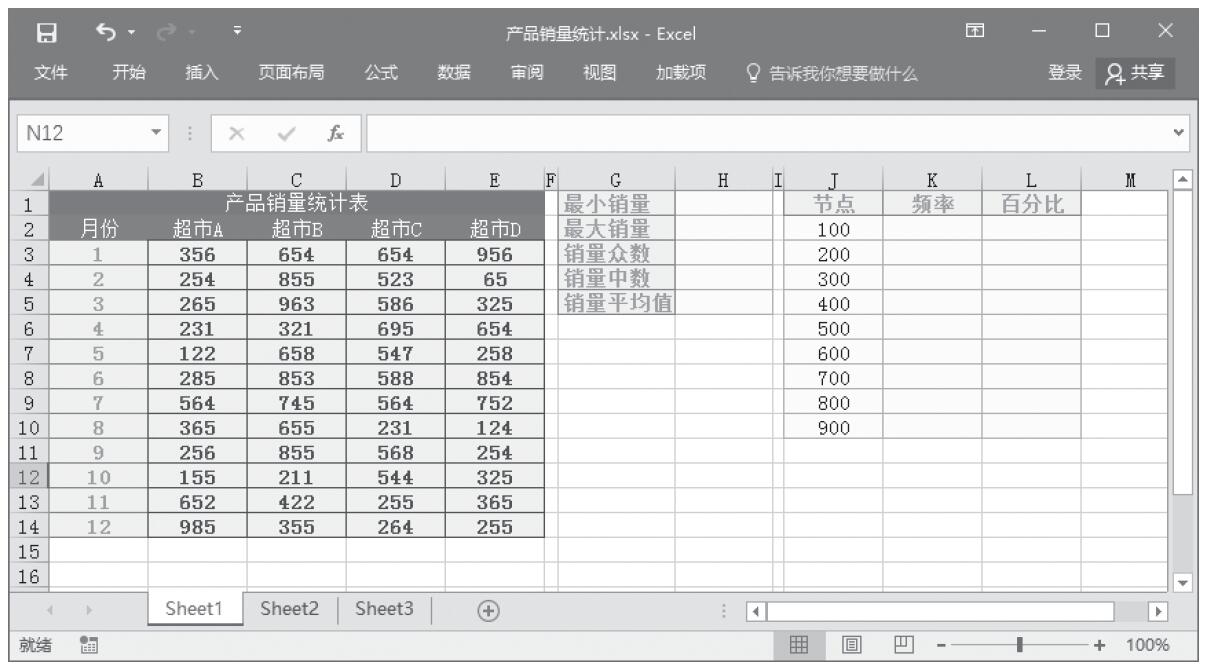
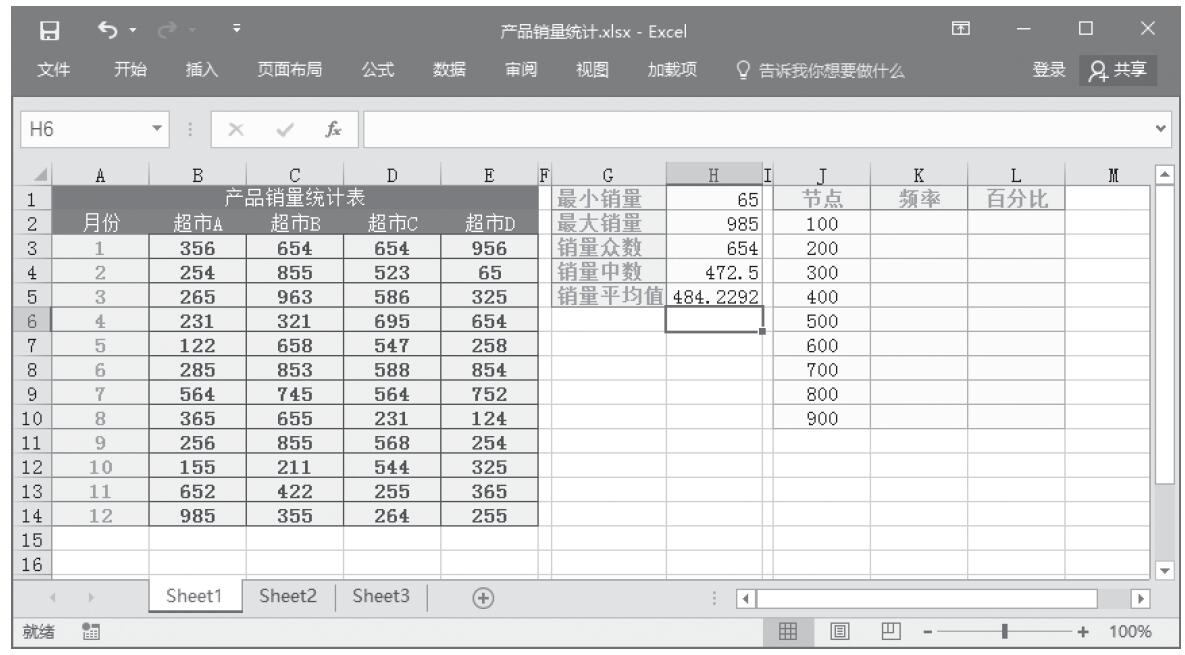
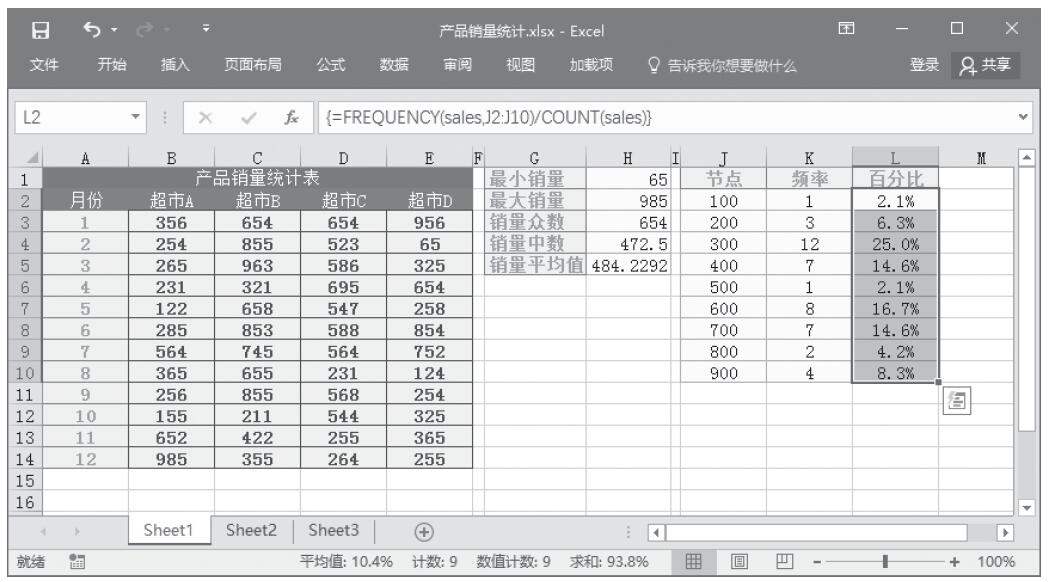
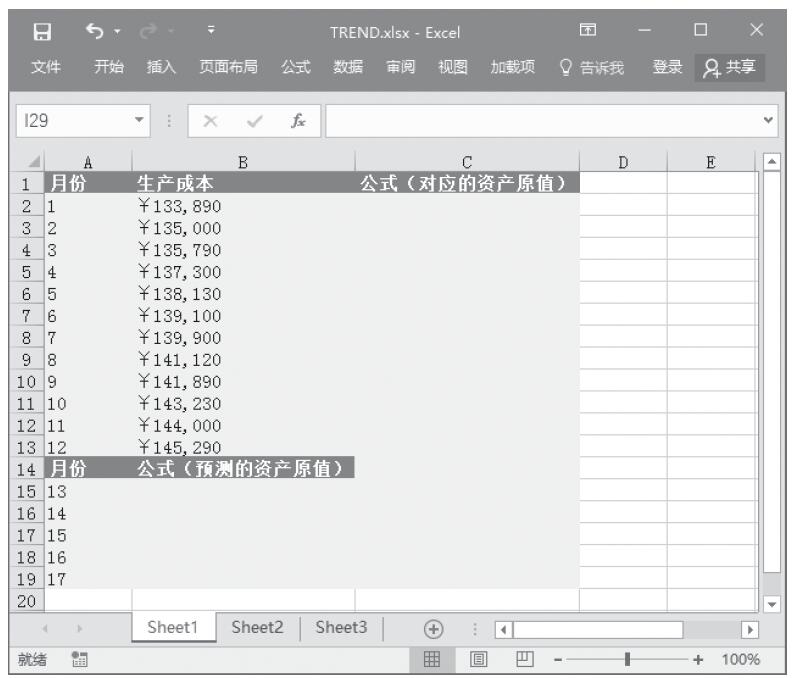
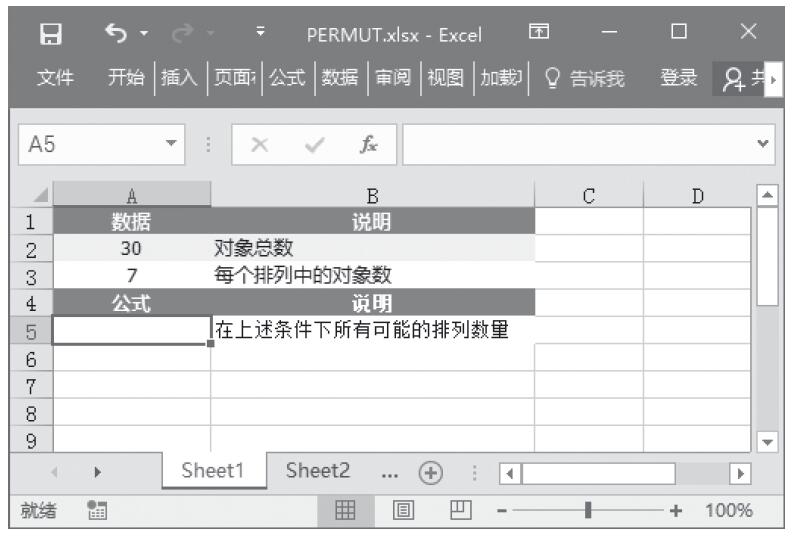
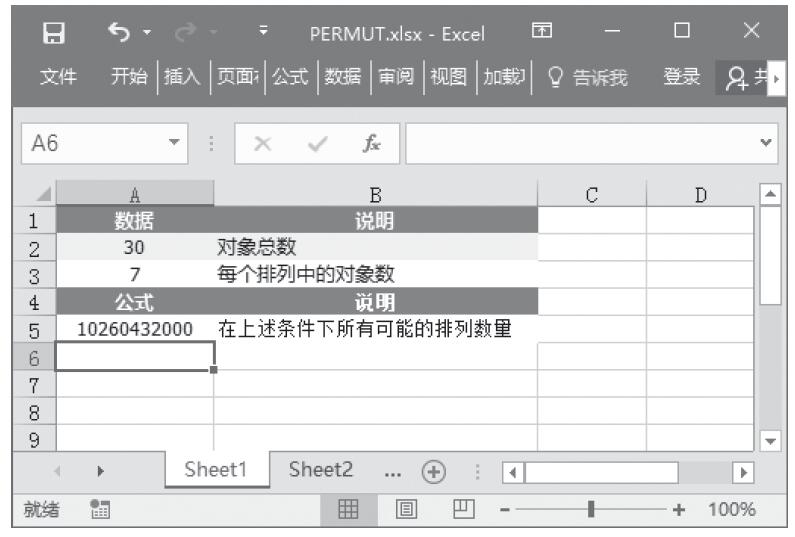
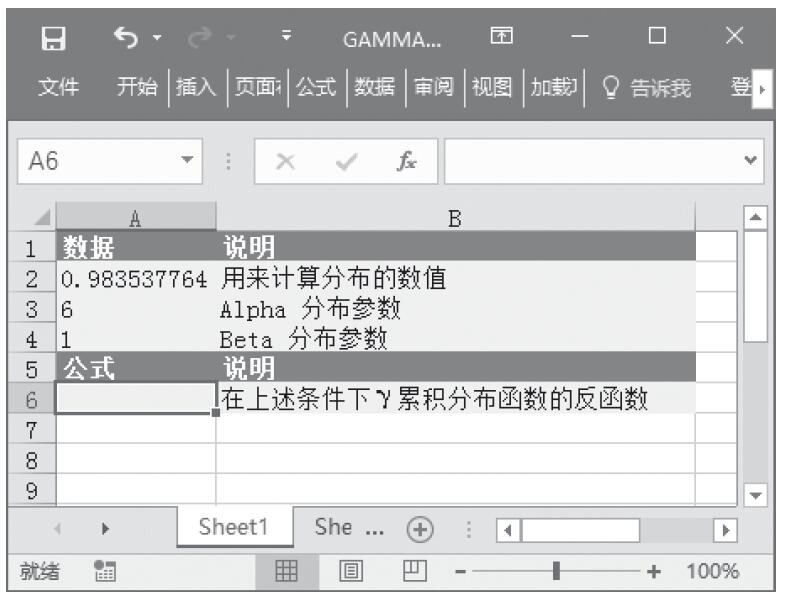
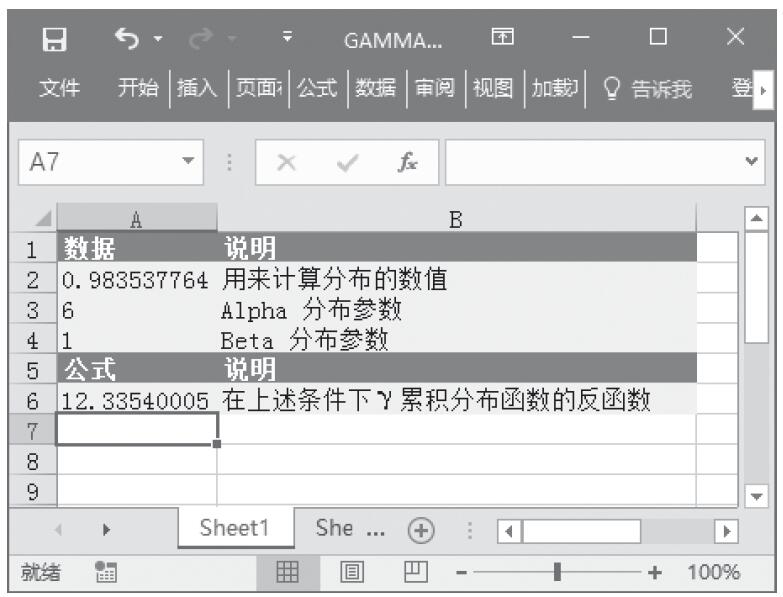
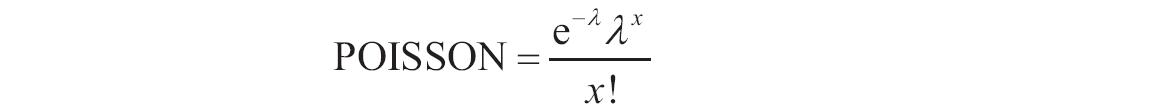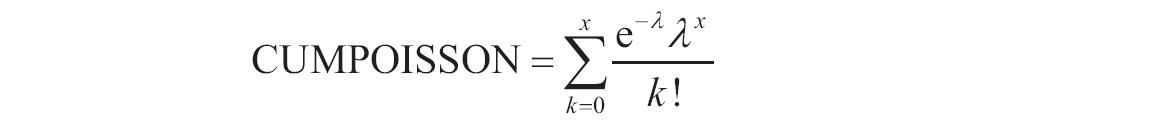某家公司向4个超市供应某种商品，统计了该商品一年中各月份在每个超市的销售量。现在欲统计商品在一年中的最小销量、最大销量、销量众数、销量中数、销量平均值，以及分段销量的频率。基础销量统计数据如图16-165所示。
图16-165 基础销量统计数据
下面根据基础销量统计数据分步详细介绍如何进行上述数据计算。
步骤1：定义数据区域。选中单元格区域“B3：E14”，然后单击“公式”选项卡中的“定义名称”按钮，打开“新建名称”对话框。
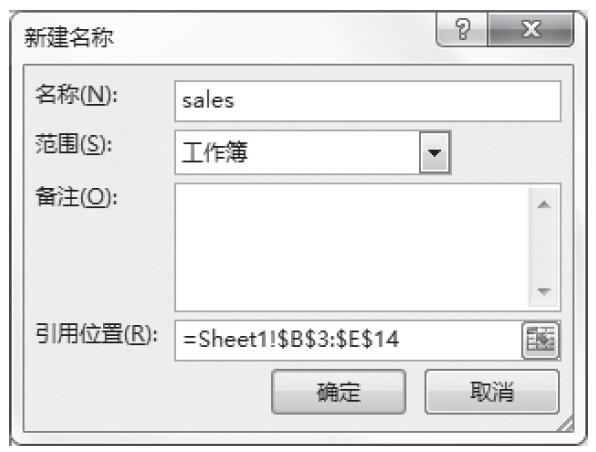
步骤2：在“名称”框中输入名称“sales”，如图16-166所示。其他选项采用默认设置。
图16-166 输入名称
步骤3：单击“确定”按钮，完成名称的定义。
步骤4：计算最小销量。在单元格H1中输入公式“=MIN（sales）”，统计一年中商品销量的最小值。
步骤5：计算最大销量。在单元格H2中输入公式“=MAX（sales）”，统计一年中商品销量的最大值。
步骤6：计算销量众数。在单元格H3中输入公式“=MODE（sales）”，统计一年中商品销量的众数。
步骤7：计算销量中数。在单元格H4中输入公式“=MEDIAN（sales）”，统计一年中商品销量的中数。
步骤8：计算销量平均值。在单元格H5中输入公式“=AVERAGE（sales）”，统计一年中商品销量的平均值。统计结果如图16-167所示。
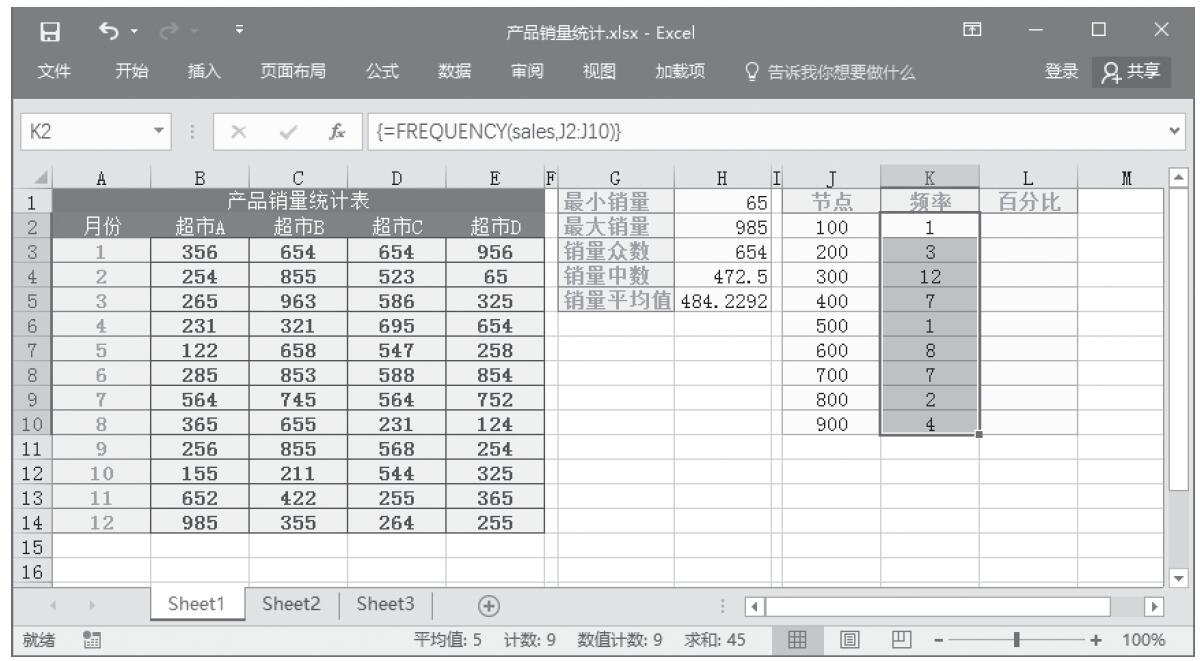
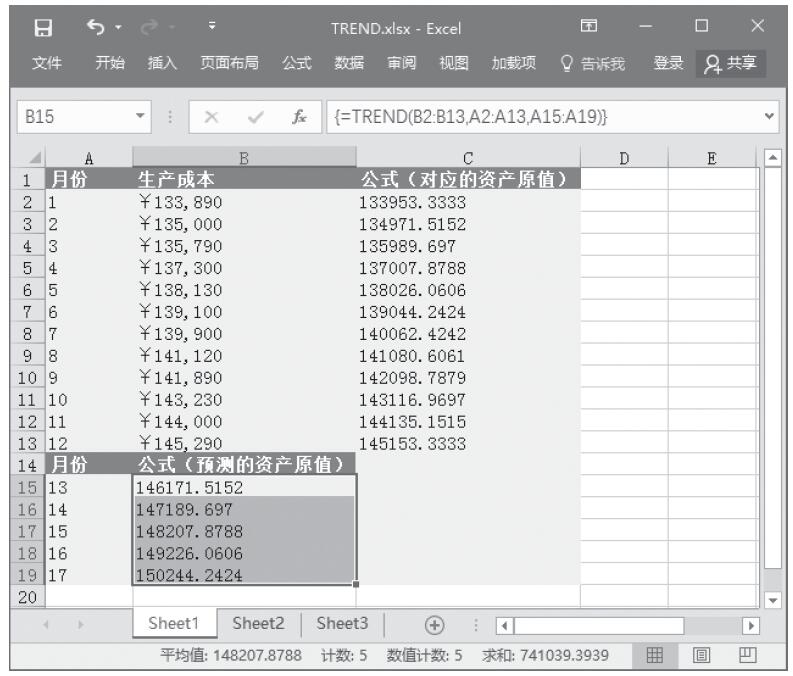
步骤9：计算分段销量的频率。选中单元格区域“K2：K10”，按F2键，然后输入公式“=FREQUENCY（sales，J2：J10）”，按“Ctrl+Shift+Enter”键以数组公式输入，结果如图16-168所示。
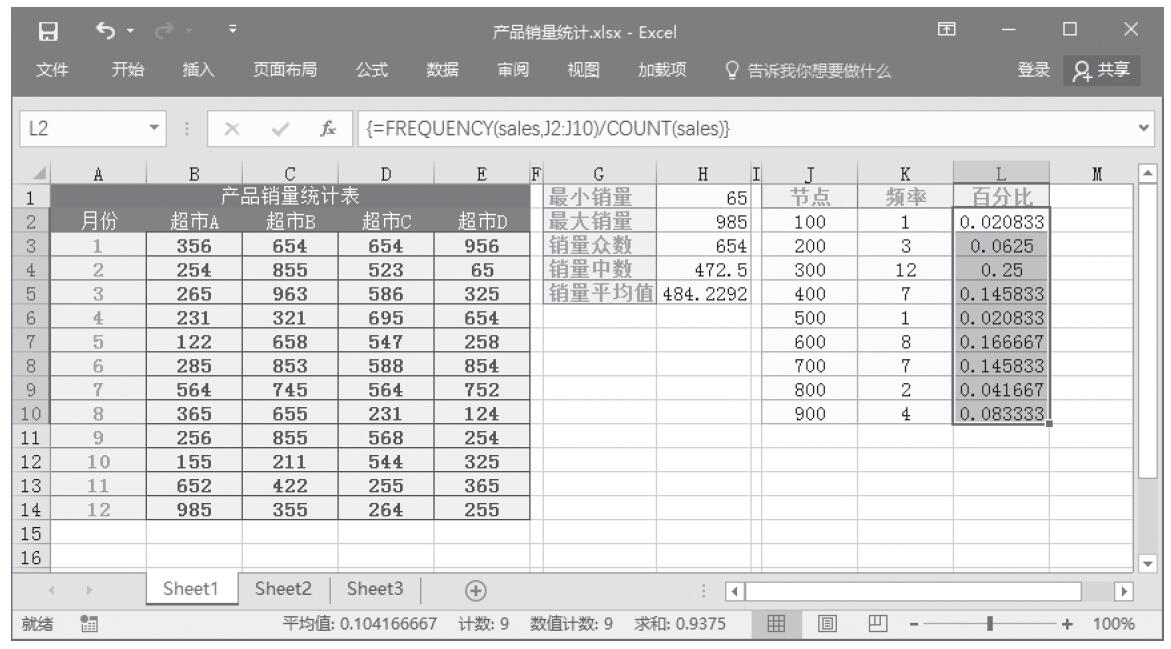
步骤10：计算分段销量的百分比。选中单元格区域L2：L10，按F2键，然后输入公式“=FREQUENCY（sales，J2：J10）/COUNT（sales）”，按“Ctrl+Shift+Enter”键以数组公式输入，结果如图16-169所示。
图16-167 统计结果
图16-168 计算分段销量的频率
图16-169 计算分段销量的百分比
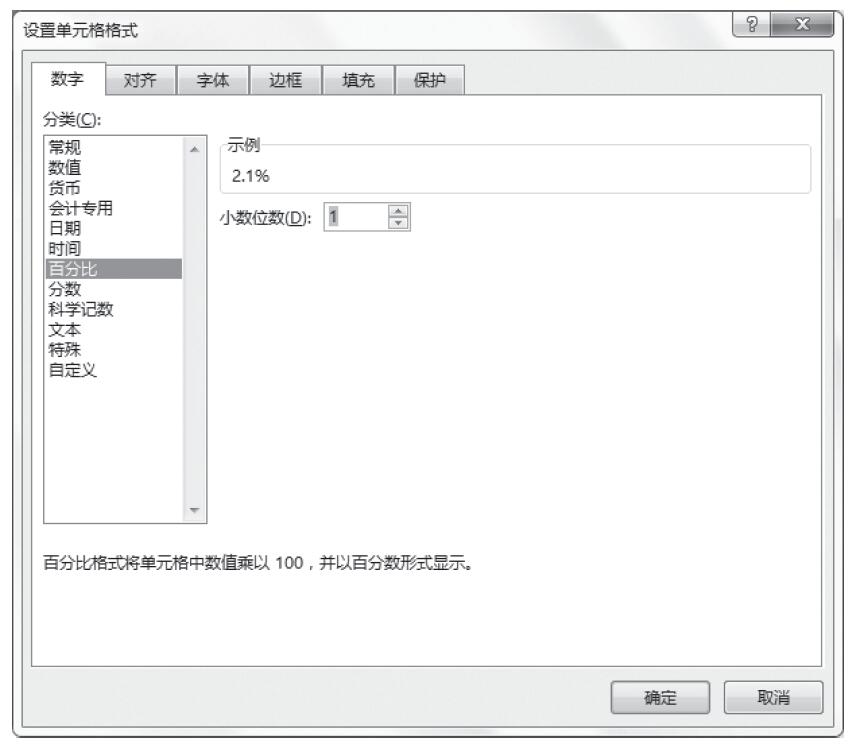
步骤11：保持单元格区域“L2：L10”的选中状态，按Ctrl+1键打开“设置单元格格式”对话框，单击“百分比”分类，然后将小数位数设置为1，如图16-170所示。
步骤12：单击“确定”按钮，得到结果如图16-171所示。
图16-170 “设置单元格格式”对话框
图16-171 分段销量的百分比
WEIBULL函数用于返回韦伯（Weibull）分布。使用此函数可以进行可靠性分析，比如计算设备的平均故障时间。WEIBULL函数的语法如下。
WEIBULL(x,alpha,beta,cumulative)
其中参数x为参数值，alpha为分布参数，beta为分布参数，cumulative为指明函数的形式。
已知参数值、Alpha分布参数、Beta分布参数，计算在这些条件下使用韦伯累积分布函数的结果和使用韦伯概率密度函数的结果。基础数据如图16-163所示。
步骤1：打开例子工作簿“WEIBULL.xlsx”。
步骤2：在单元格A6中输入公式“=WEIBULL（A2，A3，A4，TRUE）”，用于计算在上述条件下使用韦伯累积分布函数的结果。
步骤3：在单元格A7中输入公式“=WEIBULL（A2，A3，A4，FALSE）”，用于计算在上述条件下使用韦伯概率密度函数的结果。计算结果如图16-164所示。
图16-163 基础数据
图16-164 计算结果
如果x、alpha或beta为非数值型，函数WEIBULL返回错误值“#VALUE！”；如果x＜0，函数WEIBULL返回错误值“#NUM！”；如果alpha≤0或beta≤0，函数WEIBULL返回错误值“#NUM！”。韦伯累积分布函数的计算公式如下。
韦伯概率密度函数的计算公式如下。
当alpha=1，函数WEIBULL返回指数分布如下。
TREND函数用于计算一条线性回归拟合线的值。即找到适合已知数组known_y’s和known_x’s的直线（用最小二乘法），并返回指定数组new_x’s在直线上对应的y值。TREND函数的语法如下。
TREND(known_y's,known_x's,new_x's,const)
其中：
参数known_y’s是关系表达式y=mx+b中已知的y值集合。
known_x’s是关系表达式y=mx+b中已知的可选x值集合。
new_x’s为需要函数TREND返回对应y值的新x值。
const为一逻辑值，用于指定是否将常量b强制设为0。
基础数据如图16-161所示。
步骤1：打开例子工作簿“TREND.xlsx”。
步骤2：选中单元格区域C2：C13，按F2键，然后输入公式“=TREND（B2：B13，A2：A13）”，按“Ctrl+Shift+Enter”键以数组公式的形式输入，用于计算对应的资产原值。
步骤3：选中单元格区域B15：B19，按F2键，然后输入公式“=TREND（B2：B13，A2：A13，A15：A19）”，按“Ctrl+Shift+Enter”键以数组公式的形式输入，用于计算预测的资产原值。计算结果如图16-162所示。
图16-161 基础数据
图16-162 计算结果
可以使用TREND函数计算同一变量的不同乘方的回归值来拟合多项式曲线。例如，假设A列包含y值，B列含有x值。可以在C列中输入“x^2”，在D列中输入“x^3”，等等，然后根据A列，对B列到D列进行回归计算。
对于返回结果为数组的公式，必须以数组公式的形式输入。当为参数（如known_x’s）输入数组常量时，应当使用逗号分隔同一行中的数据，用分号分隔不同行中的数据。
SKEW函数用于计算分布的不对称度。不对称度反映以平均值为中心的分布的不对称程度。正不对称度表示不对称部分的分布更趋向正值，负不对称度表示不对称部分的分布更趋向负值。SKEW函数的语法如下。
SKEW(number1,number2,...)
其中参数number1，number2…为需要计算偏斜度的1到255个参数。对于参数的表示也可以不使用这种用逗号分隔参数的形式，而用单个数组或对数组的引用。
给定一组数据，计算其分布的不对称度。基础数据如图16-159所示。
步骤1：打开例子工作簿“SKEW.xlsx”。
步骤2：在单元格A13中输入公式“=SKEW（A2：A11）”，用于计算给定数据集分布的不对称度。计算结果如图16-160所示。
图16-159 基础数据
图16-160 计算结果
参数可以是数字或者是包含数字的名称、数组或引用。逻辑值和直接键入到参数列表中代表数字的文本被计算在内。如果数组或引用参数包含文本、逻辑值或空白单元格，则这些值将被忽略，但包含零值的单元格将计算在内。
如果参数为错误值或为不能转换为数字的文本，将会导致错误；如果数据点个数少于3个，或样本标准偏差为零，函数SKEW返回错误值“#DIV/0！”。不对称度的计算公式定义如下。
POISSON函数用于返回泊松分布。泊松分布通常用于预测一段时间内事件发生的次数，比如一分钟内通过收费站的轿车的数量。POISSON函数的语法如下。
POISSON(x,mean,cumulative)
其中参数x为事件数，mean为期望值。cumulative为一逻辑值，确定所返回的概率分布形式。如果cumulative为TRUE，函数POISSON返回泊松累积分布概率，即随机事件发生的次数在0到x之间（包含0和1）；如果为FALSE，则返回泊松概率密度函数，即随机事件发生的次数恰好为x。
已知事件数和期望值，计算符合这些条件的泊松累积分布概率和泊松概率密度函数的结果。基础数据如图16-157所示。
步骤1：打开例子工作簿“POISSON.xlsx”。
步骤2：在单元格A5中输入公式“=POISSON（A2，A3，TRUE）”，用于计算符合上述条件的泊松累积分布概率。
步骤3：在单元格A6中输入公式“=POISSON（A2，A3，FALSE）”，用于计算符合上述条件的泊松概率密度函数的结果。计算结果如图16-158所示。
图16-157 基础数据
图16-158 计算结果
如果x不为整数，将被截尾取整。如果x或mean为非数值型，函数POISSON返回错误值“#VALUE！”；如果x＜0，函数POISSON返回错误值“#NUM！”；如果mean＜0，函数POISSON返回错误值“#NUM！”。函数POISSON的计算公式如下。
假设cumulative=FALSE：
假设cumulative=TRUE：
PERMUT函数用于从给定数目的对象集合中选取的若干对象的排列数。排列为有内部顺序的对象或事件的任意集合或子集。排列与组合不同，组合的内部顺序无意义。此函数可用于彩票抽奖的概率计算。PERMUT函数的语法如下。
PERMUT(number,number_chosen)
其中参数number表示对象个数的整数，number_chosen表示每个排列中对象个数的整数。
已知有30个数，从中选取7个数，计算所有可能的排列数量。基础数据如图16-155所示。
步骤1：打开例子工作簿“PERMUT.xlsx”。
步骤2：在单元格A5中输入公式“=PERMUT（A2，A3）”，用于计算所有可能的排列数量。计算结果如图16-156所示。
图16-155 基础数据
图16-156 计算结果
两个参数若非整数将被截尾取整。如果number或number_chosen为非数值型，函数PERMUT返回错误值“#VALUE！”；如果number≤0或number_chosen＜0，函数PERMUT返回错误值“#NUM！”；如果number<number_chosen，函数PERMUT返回错误值“#NUM！”。排列数的计算公式如下。
PERCENTILE函数用于计算区域中数值的第k个百分点的值。可以使用此函数来建立接受阈值。例如，可以确定得分排名在10之上的CEO候选人。PERCENTILE函数的语法如下。
PERCENTILE(array,k)
其中参数array为定义相对位置的数组或数据区域。k为0到1之间的百分点值，包含0和1。
已知一组数据，计算数据在第30个百分点的值。基础数据如图16-153所示。
步骤1：打开例子工作簿“PERCENTILE.xlsx”。
步骤2：在单元格A7中输入公式“=PERCENTILE（A2：A5，0.3）”，计算结果如图16-154所示。
图16-153 基础数据
图16-154 计算结果
如果array为空或其数据点超过8191个，函数PERCENTILE返回错误值“#NUM！”；如果k为非数字型，函数PERCENTILE返回错误值“#VALUE！”；如果k＜0或k＞1，函数PERCENTILE返回错误值“#NUM！”；如果k不是1/（n-1）的倍数，函数PERCENTILE使用插值法来确定第k个百分点的值。
NEGBINOMDIST函数用于计算负二项式分布。当成功概率为常量probability_s时，函数NEGBINOMDIST返回在到达number_s次成功之前，出现number_f次失败的概率。此函数与二项式分布相似，只是它的成功次数固定，试验总数为变量。与二项式分布类似的是，试验次数被假设为自变量。NEGBINOMDIST函数的语法如下。
NEGBINOMDIST(number_f,number_s,probability_s)
其中参数number_f为失败次数，number_s为成功的极限次数，probability_s为成功的概率。
已知某种化学药剂试验的失败次数、成功的极限次数、成功的概率，计算在这些条件下的负二项式分布值。基础数据如图16-151所示。
步骤1：打开例子工作簿“NEGBINOMDIST.xlsx”。
步骤2：在单元格A6中输入公式“=NEGBINOMDIST（A2，A3，A4）”，用于计算在这些条件下的负二项式分布值。计算结果如图16-152所示。
图16-151 基础数据
图16-152 计算结果
number_f和number_s若非整数将被截尾取整。如果任一参数为非数值型，函数NEGBINOMDIST返回错误值“#VALUE！”；如果probability_s＜0或probability＞1，函数NEGBINOMDIST返回错误值“#NUM！”；如果number_f＜0或number_s＜1，函数NEGBINOMDIST返回错误值“#NUM！”。负二项式分布的计算公式如下。
式中x是number_f，r是number_s，且p是probability_s。
GAMMAINV函数用于计算γ累积分布函数的反函数。如果P=GAMMADIST（x，…），则GAMMAINV（p，…）=x。使用此函数可研究可能出现偏态分布的变量。GAMMAINV函数的语法如下。
GAMMAINV(probability,alpha,beta)
其中参数probability为γ分布的概率值，alpha为分布参数，beta为分布参数。如果beta=1，函数GAMMAINV返回标准伽玛分布。
已知用来计算分布的数值、Alpha分布参数、Beta分布参数，计算这些条件下的γ累积分布函数的反函数。基础数据如图16-149所示。
步骤1：打开例子工作簿“GAMMAINV.xlsx”。
步骤2：在单元格A6中输入公式“=GAMMAINV（A2，A3，A4）”，用于计算在上述条件下γ累积分布函数的反函数。计算结果如图16-150所示。
图16-149 基础数据
图16-150 计算结果
如果任一参数为文本型，函数GAMMAINV返回错误值“#VALUE！”；如果probability＜0或probability＞1，函数GAMMAINV返回错误值“#NUM！”；如果alpha≤0或beta≤0，函数GAMMAINV返回错误值“#NUM！”。
如果已给定概率值，则GAMMAINV使用GAMMADIST（x，alpha，beta，TRUE）=probability求解数值x。因此，GAMMAINV的精度取决于GAMMADIST的精度。GAMMAINV使用迭代搜索技术，如果搜索在100次迭代之后没有收敛，则函数返回错误值“#N/A”。