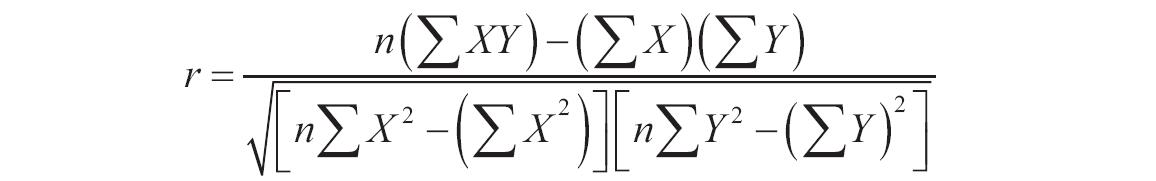分类：统计函数应用技巧

Excel中的统计函数主要用于对数据区域进行各种分类统计与分析。统计函数包括了许多统计学领域的函数，具体包括平均值函数、Beta分布函数、概率函数、单元格数量计算函数、指数与对数函数、最大值与最小值函数、标准偏差函数、方差函数、正态累积分布函数、数据集相关函数、Pearson乘积矩函数、t分布函数等。本章将通过实例介绍统计函数的基本语法、参数用法以及在实际中的应用。

Excel 应用GAMMADIST函数计算γ分布

GAMMADIST函数用于计算γ分布。可以使用此函数来研究具有偏态分布的变量。γ分布通常用于排队分析。GAMMADIST函数的语法如下。

GAMMADIST(x,alpha,beta,cumulative)

其中参数x为用来计算分布的数值，alpha为分布参数，beta为分布参数。如果beta=1，函数GAMMADIST返回标准γ分布。cumulative为一逻辑值，决定函数的形式。如果cumulative为TRUE，函数GAMMADIST返回累积分布函数；如果为FALSE，则返回概率密度函数。

典型案例

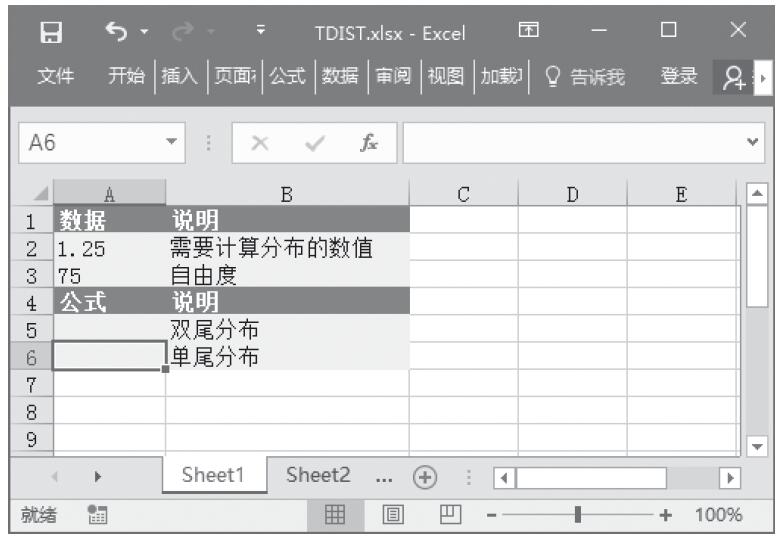
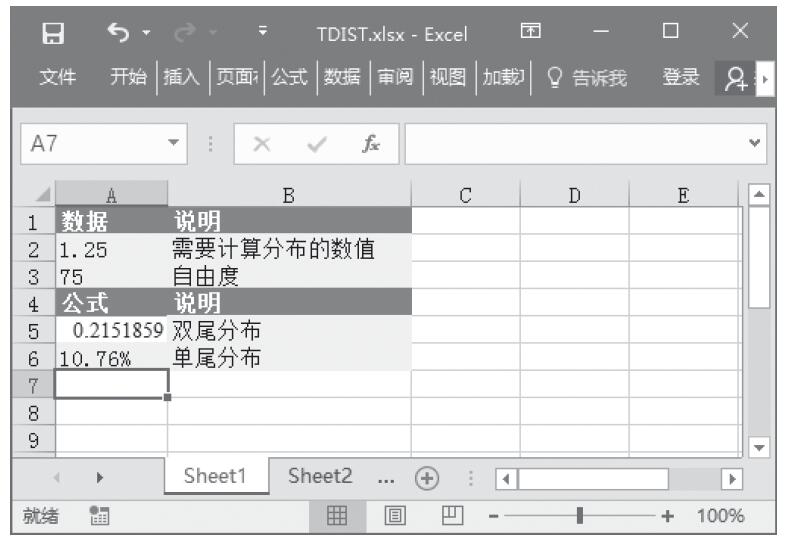
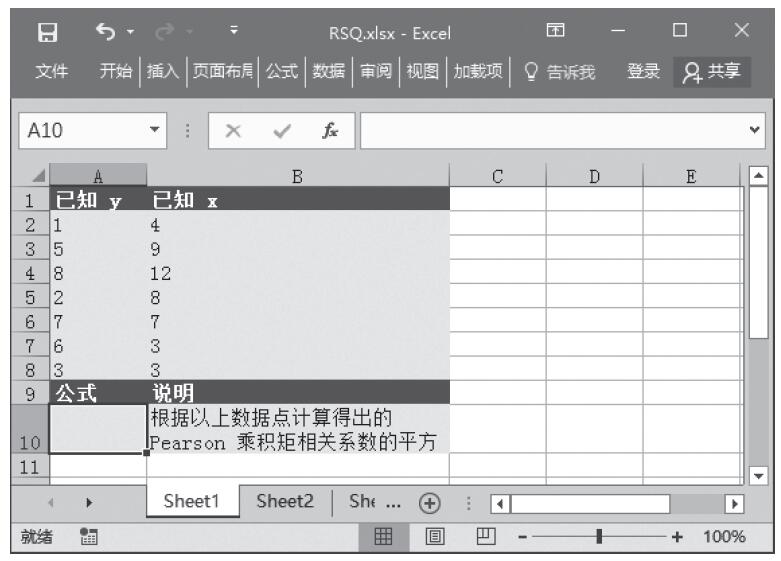
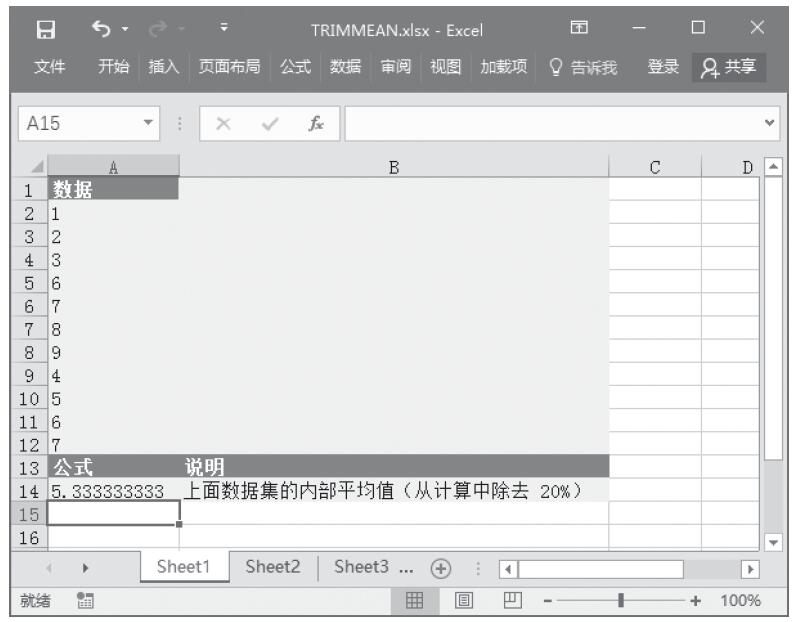
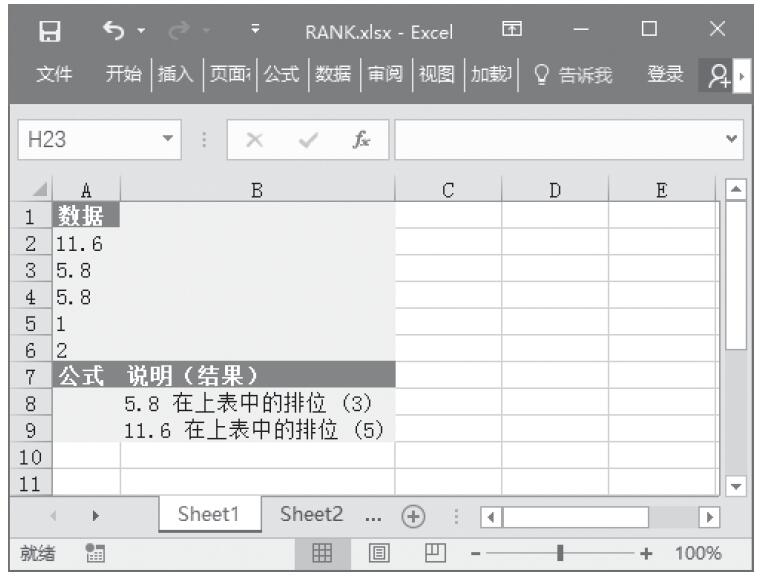
已知用来计算分布的数值、Alpha分布参数、Beta分布参数，计算这些条件下的概率γ分布和累积γ分布。基础数据如图16-147所示。

步骤1：打开例子工作簿“GAMMADIST.xlsx”。

步骤2：在单元格A6中输入公式“=GAMMADIST（A2，A3，A4，FALSE）”，用于计算在上述条件下的概率γ分布。

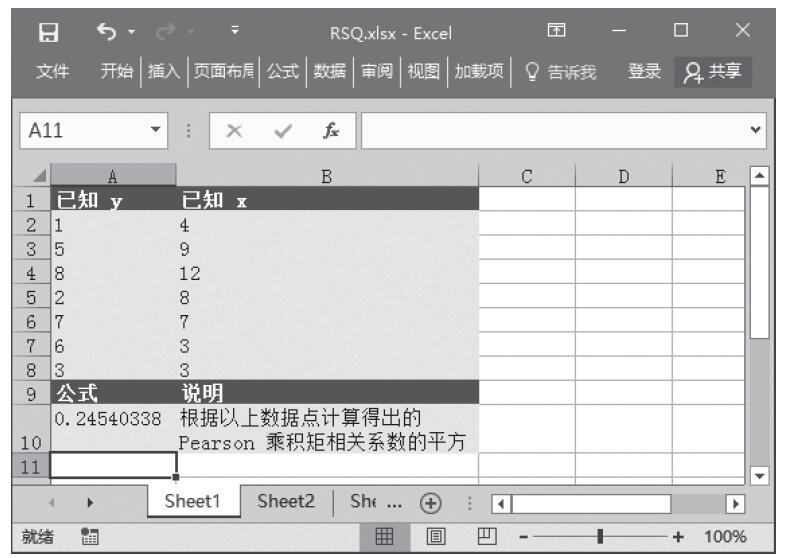
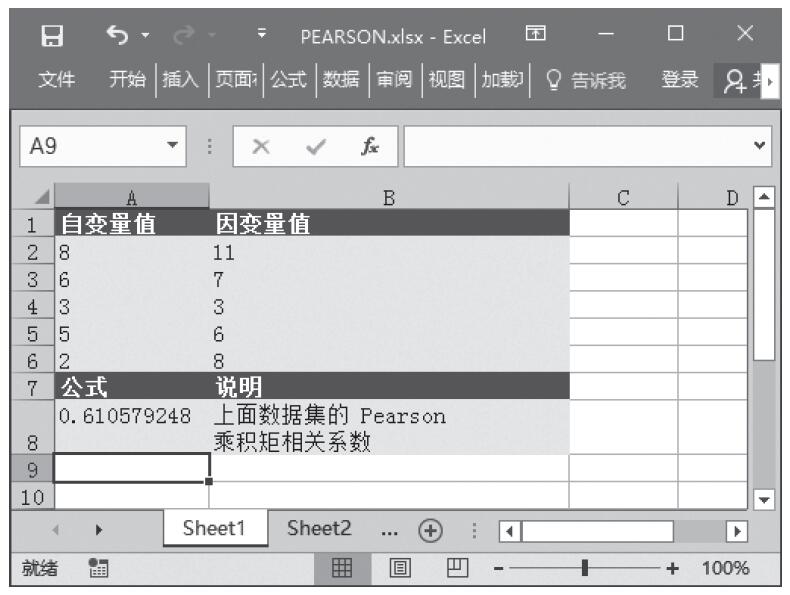
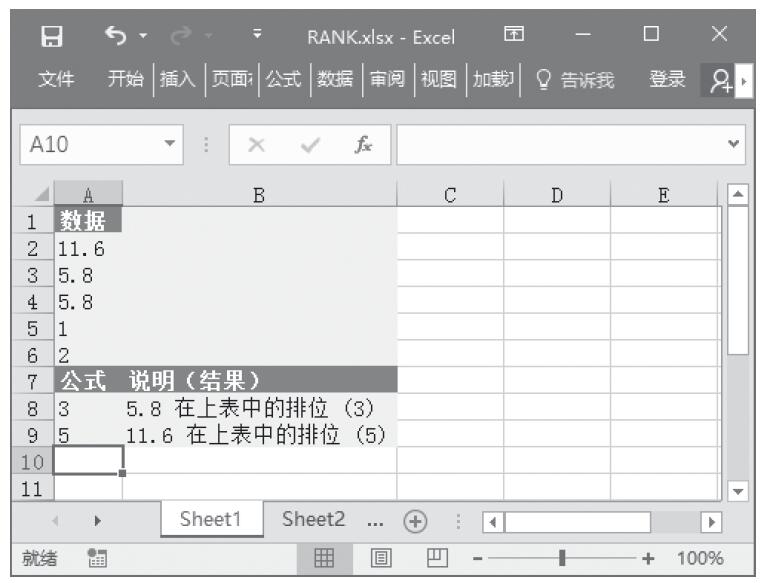
步骤3：在单元格A7中输入公式“=GAMMADIST（A2，A3，A4，TRUE）”，用于计算在上述条件下的累积γ分布。计算结果如图16-148所示。

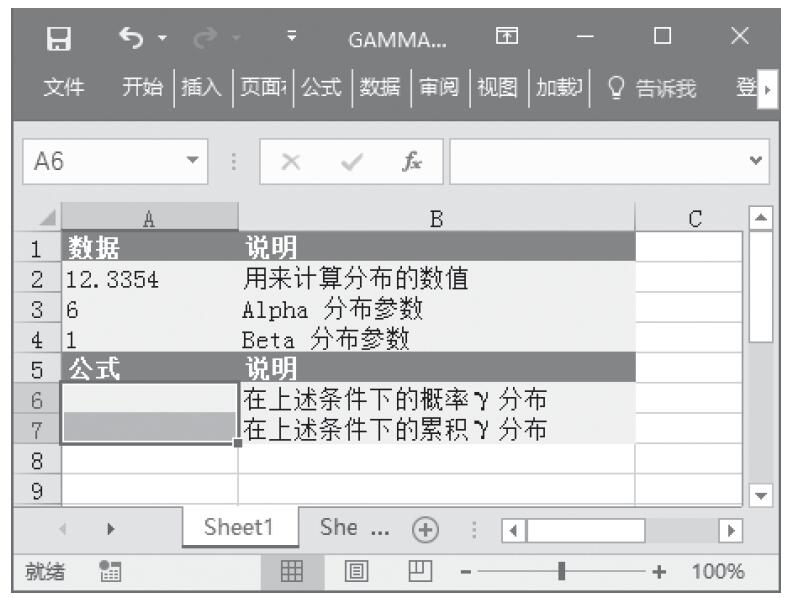
图16-147　基础数据

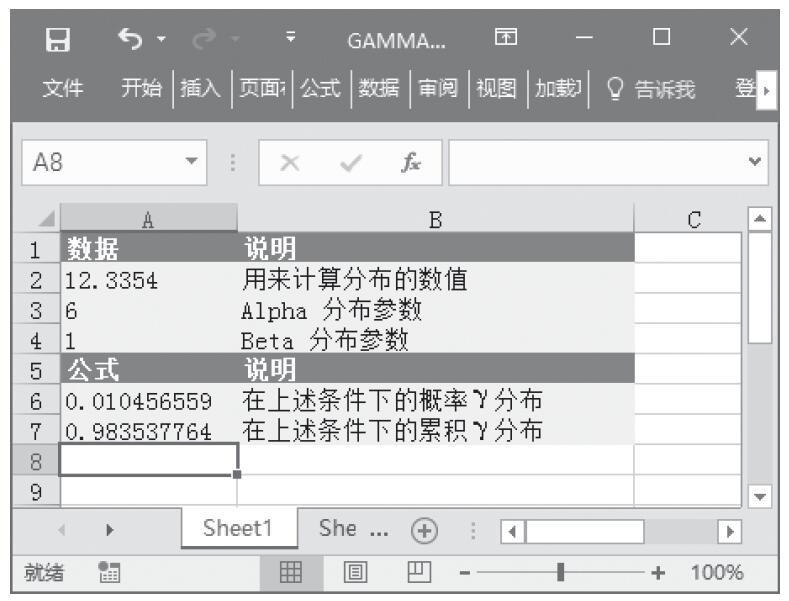
图16-148　计算结果

使用指南

如果x、alpha或beta为非数值型，函数GAMMADIST返回错误值“#VALUE！”；如果x＜0，函数GAMMADIST返回错误值“#NUM！”；如果alpha≤0或beta≤0，函数GAMMADIST返回错误值“#NUM！”。γ概率密度函数的计算公式如下。

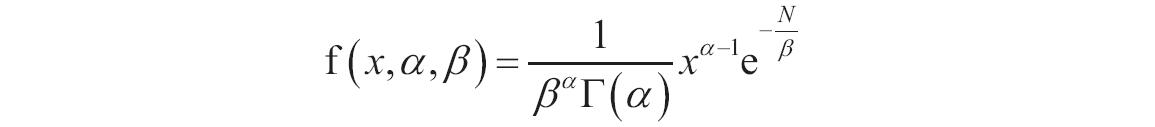
标准γ概率密度函数如下。

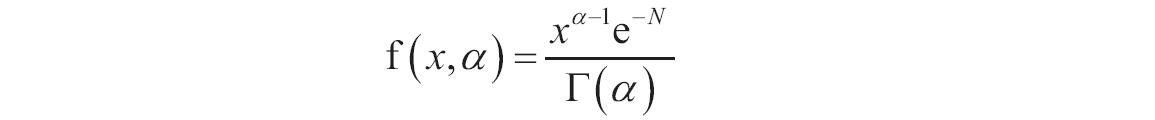
当alpha=1时，函数GAMMADIST返回如下的指数分布。

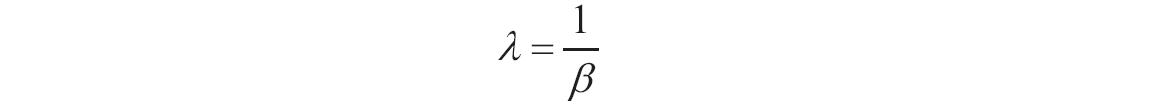
对于正整数n，当alpha=n/2，beta=2且cumulative=TRUE时，函数GAMMADIST以自由度n返回（1-CHIDIST（X））。当alpha为正整数时，函数GAMMADIST也称为爱尔朗（Erlang）分布。

Excel 应用FISHERINV函数计算Fisher变换的反函数值

FISHERINV函数用于计算Fisher变换的反函数值，使用此变换可以分析数据区域或数组之间的相关性。如果y=FISHER（x），则FISHERINV（y）=x。FISHERINV函数的语法如下。

FISHERINV(y)

其中参数y为要对其进行反变换的数值。

典型案例

计算Fisher变换的反函数在0.365463754上的值。基础数据如图16-145所示。

步骤1：打开例子工作簿“FISHERINV.xlsx”。

步骤2：在单元格A2中输入公式“=FISHERINV（0.365463754）”，用于计算Fisher变换的反函数在0.365463754上的值。计算结果如图16-146所示。

图16-145　基础数据

图16-146　计算结果

使用指南

如果y为非数值型，函数FISHERINV返回错误值“#VALUE！”。Fisher变换反函数的计算公式为：

典型案例

计算0.35的Fisher变换值。基础数据如图16-143所示。

步骤1：打开例子工作簿“FISHER.xlsx”。

步骤2：在单元格A2中输入公式“=FISHER（0.35）”，用于计算0.35的Fisher变换值。计算结果如图16-144所示。

图16-143　基础数据

图16-144　计算结果

使用指南

如果x为非数值型，函数FISHER返回错误值“#VALUE！”；如果x≤-1或x≥1，函数FISHER返回错误值“#NUM！”。Fisher变换的计算公式如下。

Excel 应用TINV函数计算学生的t分布的反函数

TINV函数用于计算作为概率和自由度函数的学生t分布的t值。TINV函数的语法如下。

TINV(probability,degrees_freedom)

其中参数probability为对应于双尾学生t分布的概率，degrees_freedom为分布的自由度数值。

典型案例

已知对应于双尾学生t分布的概率和自由度，计算学生t分布的t值。基础数据如图16-141所示。

步骤1：打开例子工作簿“TINV.xlsx”。

步骤2：在单元格A5中输入公式“=TINV（A2，A3）”，用于计算学生t分布的t值。计算结果如图16-142所示。

图16-141　基础数据

图16-142　计算结果

使用指南

如果任一参数为非数值型，函数TINV返回错误值“#VALUE！”；如果probability＜0或probability＞1，函数TINV返回错误值“#NUM！”；如果degrees_freedom不是整数，将被截尾取整；如果degrees_freedom＜1，函数TINV返回错误值“#NUM！”。TINV返回t值，P（|X|＞t）=probability，其中X为服从t分布的随机变量，且P（|X|＞t）=P（X<-t or X＞t）。

单尾t值可通过用两倍概率替换概率而求得。如果概率为0.05而自由度为10，则双尾值由TINV（0.05，10）计算得到，它返回2.28139。而同样概率和自由度的单尾值可由TINV（2*0.05，10）计算得到，它返回1.812462。在某些表中，概率被描述为（1-p）。

如果已给定概率值，则TINV使用TDIST（x，degrees_freedom，2）=probability求解数值x。因此，TINV的精度取决于TDIST的精度。TINV使用迭代搜索技术，如果搜索在100次迭代之后没有收敛，则函数返回错误值“#N/A”。

Excel 应用TDIST函数计算学生的t分布

TDIST函数用于计算学生t分布的百分点（概率），其中数值（即x）是t的计算值（将计算其百分点）。t分布用于小样本数据集合的假设检验，使用此函数可以代替t分布的临界值表。TDIST函数的语法如下。

TDIST(x,degrees_freedom,tails)

其中参数x是需要计算分布的数值，degrees_freedom是一个表示自由度的整数，tails指定返回的分布函数是单尾分布还是双尾分布。如果tails=1，则TDIST返回单尾分布；如果tails=2，则TDIST返回双尾分布。

典型案例

已知需要计算分布的数值和自由度，计算双尾分布和单尾分布。基础数据如图16-139所示。

步骤1：打开例子工作簿“TDIST.xlsx”。

步骤2：在单元格A5中输入公式“=TDIST（A2，A3，2）”，用于计算双尾分布。

步骤3：在单元格A6中输入公式“=TDIST（A2，A3，1）”，用于计算单尾分布。计算结果如图16-140所示。

图16-139　基础数据

图16-140　计算结果

使用指南

如果任一参数为非数字型，则TDIST返回错误值“#VALUE！”。如果degrees_freedom＜1，则TDIST返回错误值“#NUM！”。参数degrees_freedom和tails若不是整数将被截尾取整。如果tails不为1或2，则TDIST返回错误值“#NUM！”。如果x＜0，TDIST返回错误值“#NUM！”。

如果tails=1，TDIST的计算公式为TDIST=P（X＞x），其中X为服从t分布的随机变量；如果tails=2，TDIST的计算公式为TDIST=P（|X|＞x）=P（X＞x or X＜-x）。因为不允许x＜0，所以当x＜0时要使用TDIST，注意用TDIST（-x，df，1）=1–TDIST（x，df，1）=P（X＞-x）和TDIST（-x，df，2）=TDIST（xdf，2）=P（|X|＞x）进行变形换算。

Excel 应用RSQ函数计算Pearson乘积矩相关系数的平方

RSQ函数用于根据known_y’s和known_x’s中数据点计算得出的Pearson乘积矩相关系数的平方。R平方值可以解释为y方差与x方差的比例。RSQ函数的语法如下。

RSQ(known_y's,known_x's)

其中参数known_y’s为因变量数组或数据点区域。known_x’s为自变量数组或数据点区域。

典型案例

已知一组x值和y值，计算Pearson乘积矩相关系数的平方。基础数据如图16-137所示。

步骤1：打开例子工作簿“RSQ.xlsx”。

步骤2：在单元格A10中输入公式“=RSQ（A2：A8，B2：B8）”，用于根据以上数据点计算得出的Pearson乘积矩相关系数的平方。计算结果如图16-138所示。

图16-137　基础数据

图16-138　计算结果

使用指南

参数可以是数字或者是包含数字的名称、数组或引用。逻辑值和直接键入到参数列表中代表数字的文本被计算在内。如果数组或引用参数包含文本、逻辑值或空白单元格，则这些值将被忽略，但包含零值的单元格将计算在内。如果参数为错误值或为不能转换成数字的文本，将会导致错误；如果known_y’s和known_x’s为空或其数据点个数不同，函数RSQ返回错误值“#N/A”；如果known_y’s和known_x’s函数只包含1个数据点，则RSQ函数返回错误值“#DIV/0！”。Pearson乘积矩相关系数r的计算公式如下。

其中X和Y是样本平均值AVERAGE（known_x’s）和AVERAGE（known_y’s）。RSQ返回r²，即相关系数的平方。

Excel 应用PEARSON函数计算Pearson乘积矩相关系数

PEARSON函数用于返回Pearson（皮尔森）乘积矩相关系数r，这是一个范围在-1.0到1.0之间（包括-1.0和1.0）的无量纲指数，反映了两个数据集合之间的线性相关程度。PEARSON函数的语法如下。

PEARSON(array1,array2)

其中参数array1为自变量集合，array2为因变量集合。

典型案例

已知一组自变量值和因变量值，计算数据集的Pearson乘积矩相关系数。基础数据如图16-135所示。

步骤1：打开例子工作簿“PEARSON.xlsx”。

步骤2：在单元格A8中输入公式“=PEARSON（A2：A6，B2：B6）”，计算结果如图16-136所示。

图16-135　基础数据

图16-136　计算结果

使用指南

参数可以是数字，或者是包含数字的名称、数组常量或引用。如果数组或引用参数包含文本、逻辑值或空白单元格，则这些值将被忽略，但包含零值的单元格将计算在内。如果array1和array2为空或其数据点个数不同，函数PEARSON返回错误值“#N/A”。Pearson乘积矩相关系数r的公式如下。

其中X和Y是样本平均值AVERAGE（array1）和AVERAGE（array2）。

Excel 应用TRIMMEAN函数计算数据集的内部平均值

TRIMMEAN函数用于计算数据集的内部平均值。函数TRIMMEAN先从数据集的头部和尾部除去一定百分比的数据点，然后再求平均值。当希望在分析中剔除一部分数据的计算时，可以使用此函数。TRIMMEAN函数的语法如下。

TRIMMEAN(array,percent)

其中参数array为需要进行整理并求平均值的数组或数值区域，percent为计算时所要除去的数据点的比例。例如，如果percent=0.2，在20个数据点的集合中，就要除去4个数据点（20×0.2）：头部除去2个，尾部除去2个。

典型案例

已知一组数据，计算其内部平均值。基础数据如图16-133所示。

步骤1：打开例子工作簿“TRIMMEAN.xlsx”。

步骤2：在单元格A14中输入公式“=TRIMMEAN（A2：A12，0.2）”，用于计算数据集的内部平均值（从计算中除去20%）。计算结果如图16-134所示。

图16-133　基础数据

图16-134　计算结果

使用指南

如果percent<0或percent>1，函数TRIMMEAN返回错误值“#NUM！”。函数TRIMMEAN将除去的数据点数目向下舍入为最接近的2的倍数。例如，如果percent=0.1，30个数据点的10%等于3个数据点。函数TRIMMEAN将会把除去的数据点数目向下舍入为2，并对称地在数据集的头部和尾部各除去一个数据。

Excel 应用RANK函数计算一个数字在数字列表中的排位

RANK函数用于计算一个数字在数字列表中的排位。数字的排位是其大小与列表中其他值的比值（如果列表已排过序，则数字的排位就是它当前的位置）。RANK函数的语法如下。

RANK(number,ref,order)

其中参数number为需要找到排位的数字。ref为数字列表数组或对数字列表的引用，其中的非数值型参数将被忽略。order为一数字，指明排位的方式。如果order为0（零）或省略，Excel对数字的排位是基于ref为按照降序排列的列表；如果order不为零，Excel对数字的排位是基于ref为按照升序排列的列表。

典型案例

已知一组数据，计算指定数值在数据集中的排位。基础数据如图16-131所示。

步骤1：打开例子工作簿“RANK.xlsx”。

步骤2：在单元格A8中输入公式“=RANK（A3，A2：A6，1）”，用于计算5.8在上表中的排位。

步骤3：在单元格A9中输入公式“=RANK（A2，A2：A6，1）”，用于计算11.6在上表中的排位。计算结果如图16-132所示。

图16-131　基础数据

图16-132　计算结果

使用指南

1）函数RANK对重复数的排位相同。但重复数的存在将影响后续数值的排位。例如，在一列按升序排列的整数中，如果整数10出现两次，其排位为5，则11的排位为7（没有排位为6的数值）。

2）由于某些原因，用户可能使用考虑重复数字的排位定义。在前面的示例中，用户可能要将整数10的排位改为5.5。这可通过将下列修正因素添加到按排位返回的值来实现。该修正因素对于按照升序计算排位（顺序为非零值）或按照降序计算排位（顺序为0或被忽略）的情况都是正确的。

3）重复数排位的修正因素=[COUNT（ref）+1–RANK（number，ref，0）–RANK（number，ref，1）]÷2。

4）在上面的示例中，RANK（A2，A1：A5，1）等于3。修正因素是（5+1–2–3）÷2=0.5，考虑重复数排位的修改排位是3+0.5=3.5。如果数字仅在ref出现一次，由于不必调整RANK，因此修正因素为0。

Excel 应用QUARTILE函数计算数据集的四分位数

QUARTILE函数用于计算数据集的四分位数。四分位数通常用于在销售额和测量数据中对总体进行分组。例如，我们可以使用函数QUARTILE求得总体收入中前25%的收入值。QUARTILE函数的语法如下。

QUARTILE(array,quart)

其中参数array为需要求得四分位数值的数组或数字型单元格区域，quart用于决定返回哪一个四分位值。

典型案例

已知一组数据，计算第一个四分位数，即第25个百分点值。基础数据如图16-129所示。

步骤1：打开例子工作簿“QUARTILE.xlsx”。

步骤2：在单元格A11中输入公式“=QUARTILE（A2：A9，1）”，用于计算第一个四分位数。计算结果如图16-130所示。

图16-129　基础数据

图16-130　计算结果

使用指南

如果数组为空，函数QUARTILE返回错误值“#NUM！”；如果quart不为整数，将被截尾取整；如果quart<0或quart>4，函数QUARTILE返回错误值“#NUM！”。当quart分别等于0、2和4时，函数MIN、MEDIAN和MAX返回的值与函数QUARTILE返回的值相同。