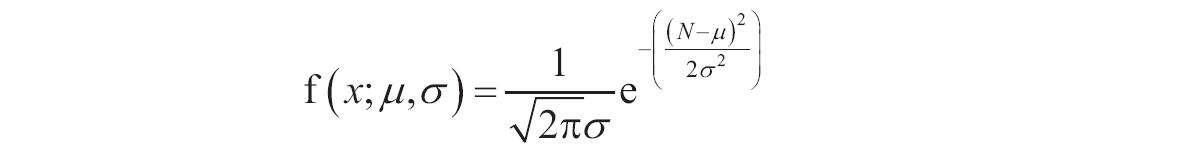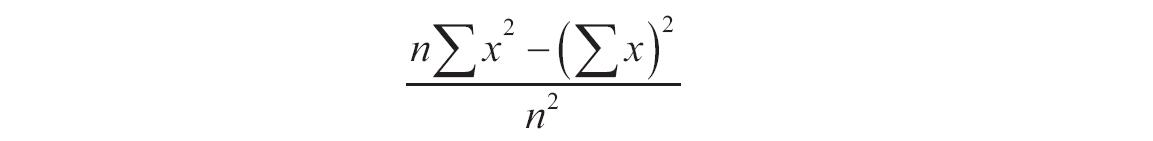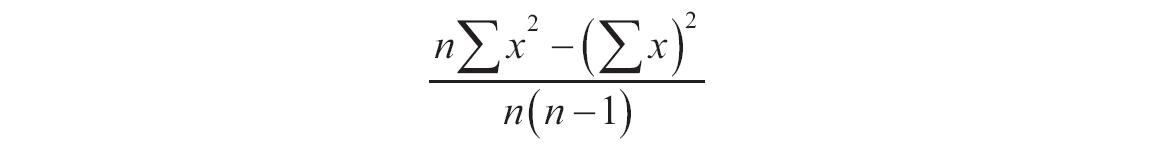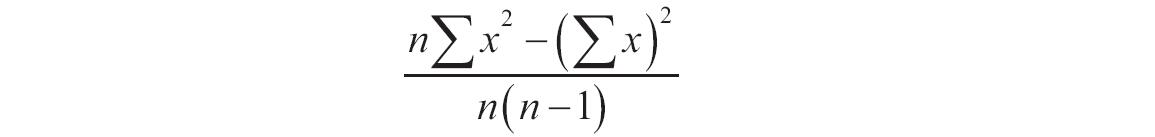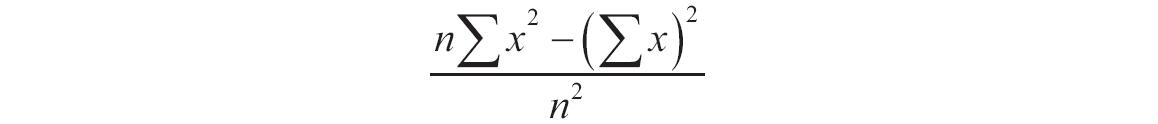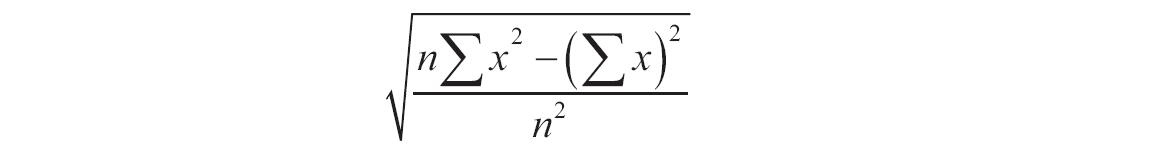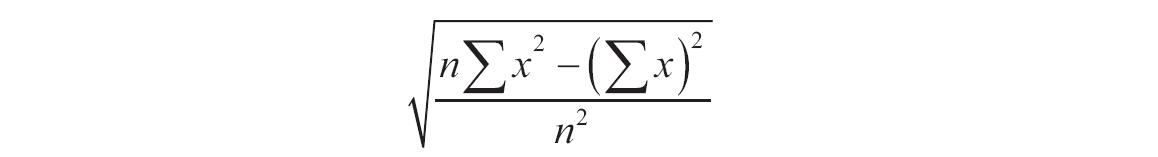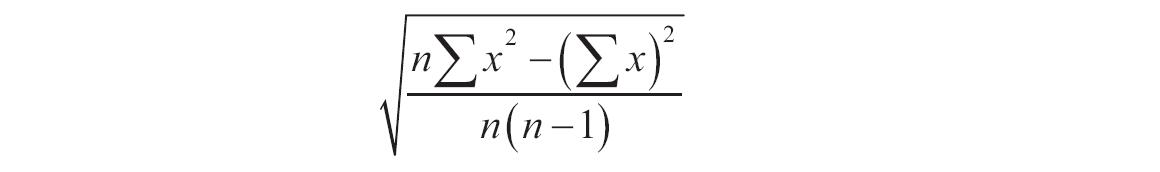Excel中的统计函数主要用于对数据区域进行各种分类统计与分析。统计函数包括了许多统计学领域的函数，具体包括平均值函数、Beta分布函数、概率函数、单元格数量计算函数、指数与对数函数、最大值与最小值函数、标准偏差函数、方差函数、正态累积分布函数、数据集相关函数、Pearson乘积矩函数、t分布函数等。本章将通过实例介绍统计函数的基本语法、参数用法以及在实际中的应用。
NORMSDIST函数用于计算标准正态累积分布函数，该分布的平均值为0，标准偏差为1。可以使用该函数代替标准正态曲线面积表。NORMSDIST函数的语法如下。
NORMSDIST(z)
其中参数z为需要计算其分布的数值。
计算1.66667的正态累积分布函数值。基础数据如图16-107所示。
步骤1：打开例子工作簿“NORMSDIST.xlsx”。
步骤2：在单元格A2中输入公式“=NORMSDIST（1.66667）”，用于计算1.66667的正态累积分布函数值。计算结果如图16-108所示。
图16-107 基础数据
图16-108 计算结果
如果z为非数值型，函数NORMSDIST返回错误值“#VALUE！”。标准正态分布密度函数计算公式如下：
NORMINV函数用于计算指定平均值和标准偏差的正态累积分布函数的反函数。NORMINV函数的语法如下。
NORMINV(probability,mean,standard_dev)
其中参数probability为正态分布的概率值，mean为分布的算术平均值，standard_dev为分布的标准偏差。
已知需要计算其分布的数值、分布的算术平均值和分布的标准偏差，计算在这些条件下正态累积分布函数的反函数值。基础数据如图16-105所示。
步骤1：打开例子工作簿“NORMINV.xlsx”。
步骤2：在单元格A6中输入公式“=NORMINV（A2，A3，A4）”，用于计算正态累积分布函数的反函数值。计算结果如图16-106所示。
图16-105 基础数据
图16-106 计算结果
如果任一参数为非数值型，函数NORMINV返回错误值“#VALUE！”；如果probability＜0或probability＞1，函数NORMINV返回错误值“#NUM！”；如果standard_dev≤0，函数NORMINV返回错误值“#NUM！”；如果mean=0且standard_dev=1，函数NORMINV使用标准正态分布。
如果已给定概率值，则NORMINV使用NORMDIST（x，mean，standard_dev，TRUE）=probability求解数值x。因此，NORMINV的精度取决于NORMDIST的精度。NORMINV使用迭代搜索技术，如果搜索在100次迭代之后没有收敛，则函数返回错误值“#N/A”。
NORMDIST函数用于计算指定平均值和标准偏差的正态分布函数。此函数在统计方面应用范围广泛（包括假设检验）。NORMDIST函数的语法如下。
NORMDIST(x,mean,standard_dev,cumulative)
其中参数x为需要计算其分布的数值，mean为分布的算术平均值，standard_dev为分布的标准偏差，cumulative为一决定函数形式的逻辑值。如果cumulative为TRUE，函数NORMDIST返回累积分布函数；如果为FALSE，返回概率密度函数。
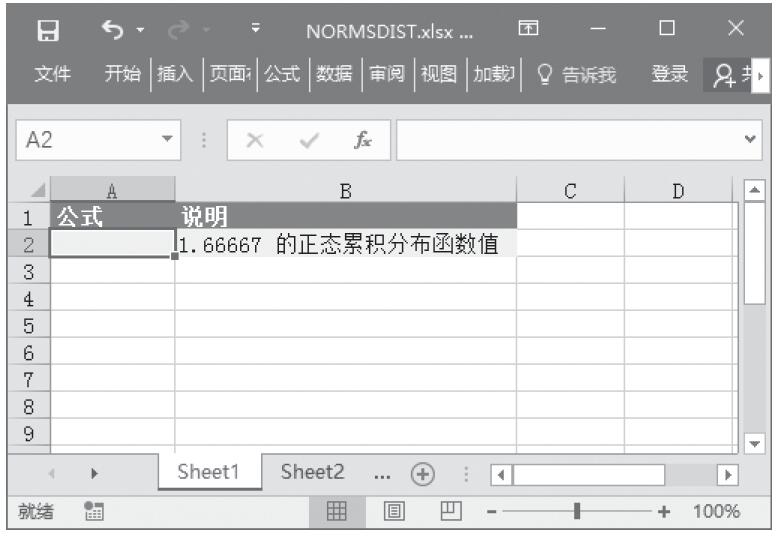
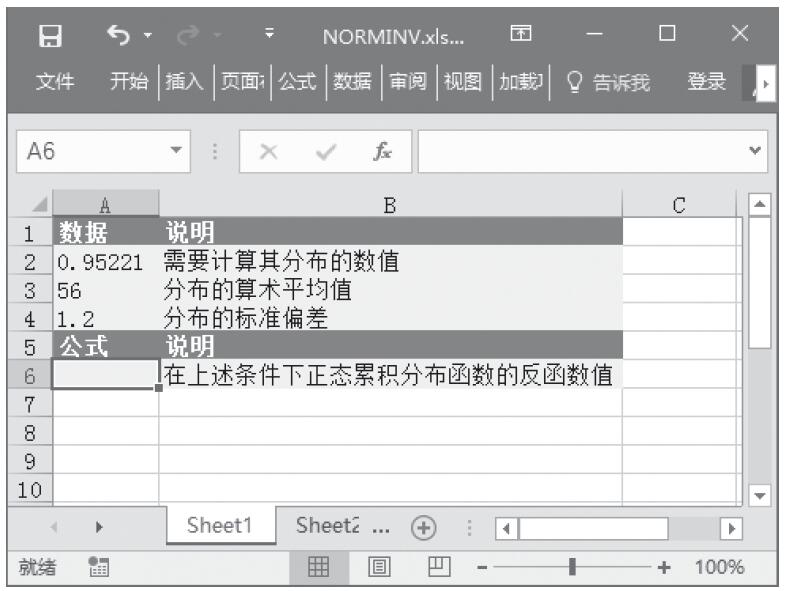
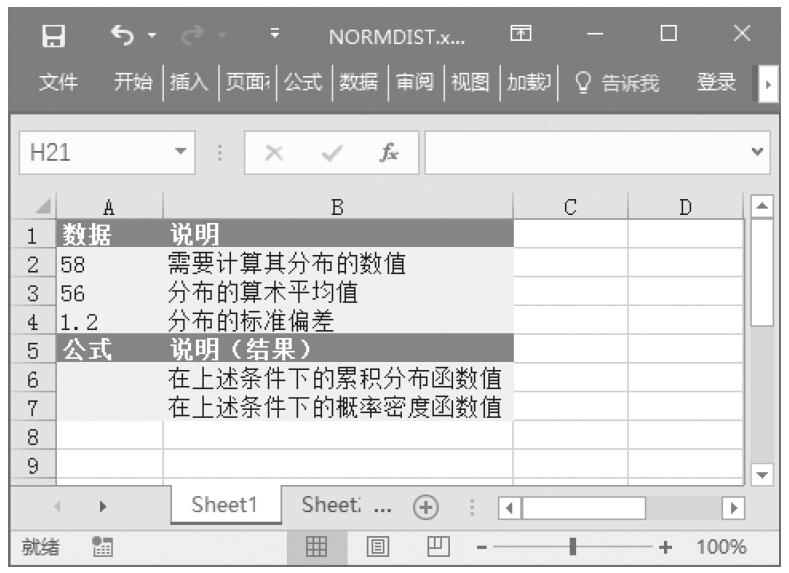
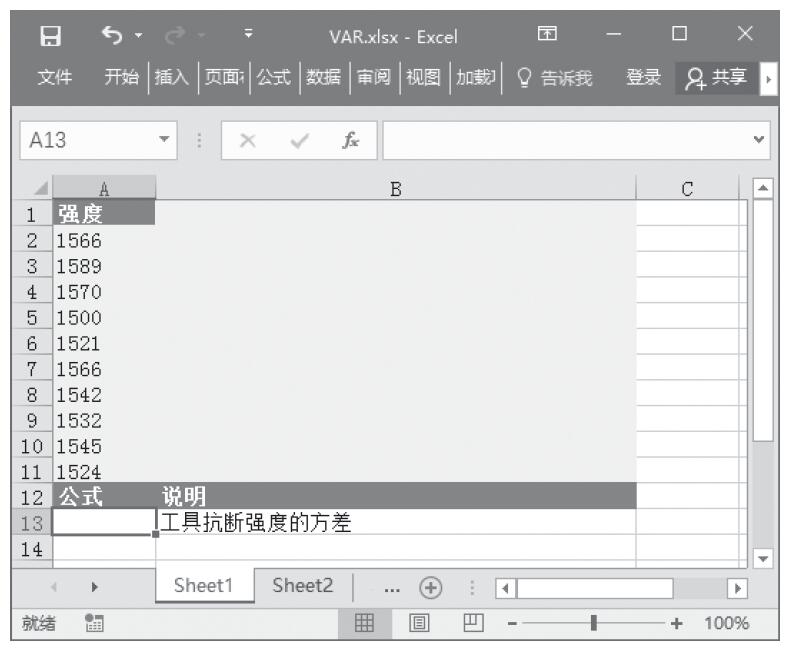
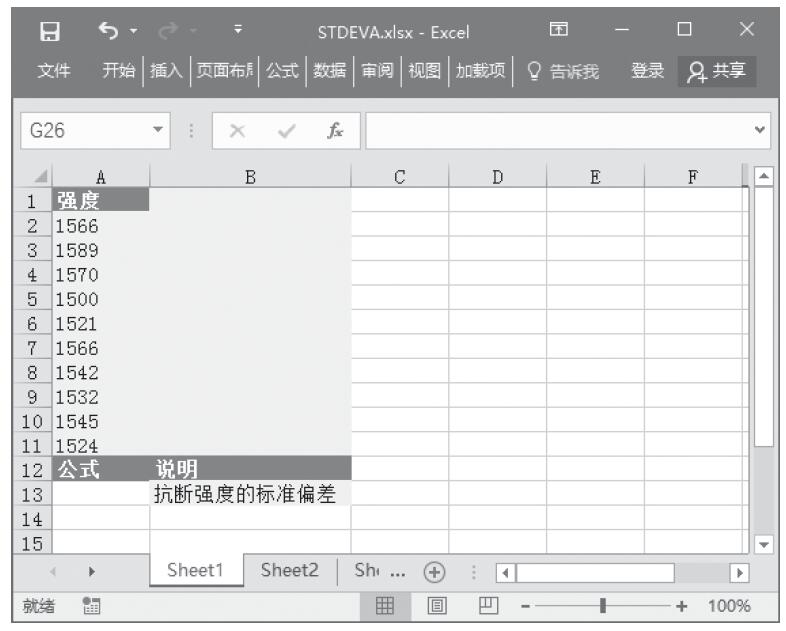
已知需要计算其分布的数值、分布的算术平均值和分布的标准偏差，计算累积分布函数值和概率密度函数值。基础数据如图16-103所示。
步骤1：打开例子工作簿“NORMDIST.xlsx”。
步骤2：在单元格A6中输入公式“=NORMDIST（A2，A3，A4，TRUE）”，用于计算在上述条件下的累积分布函数值。
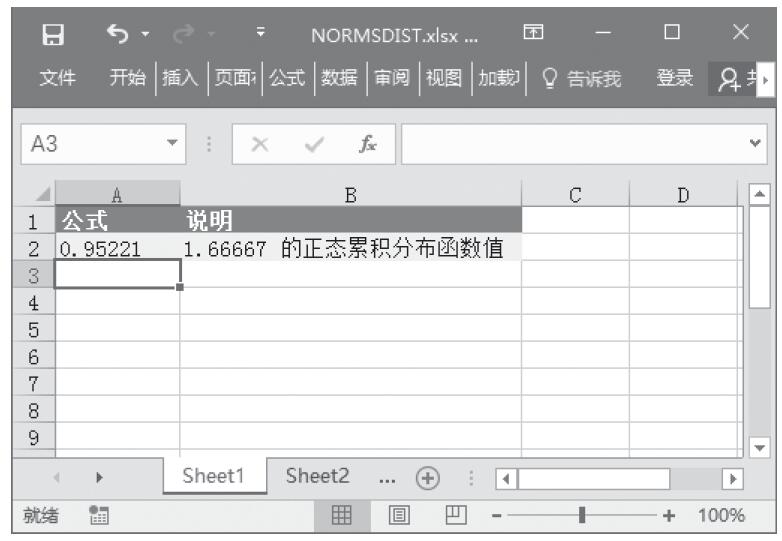
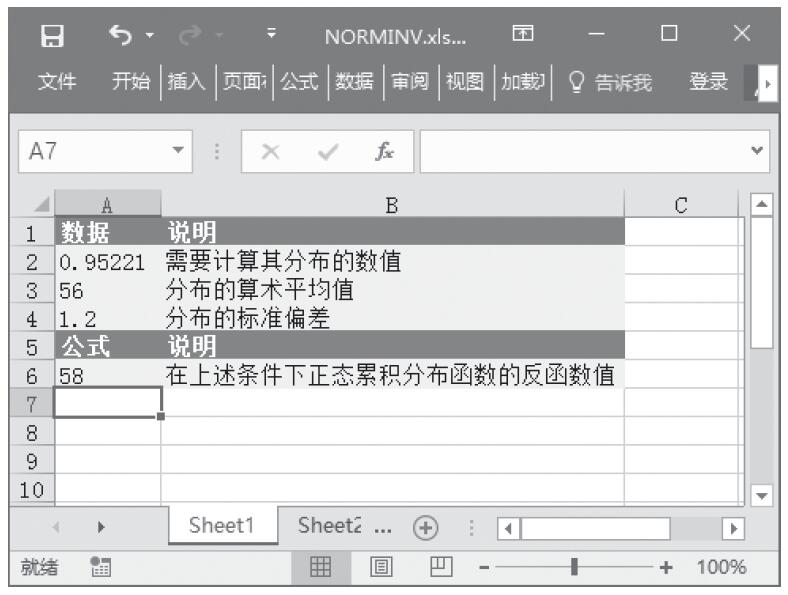
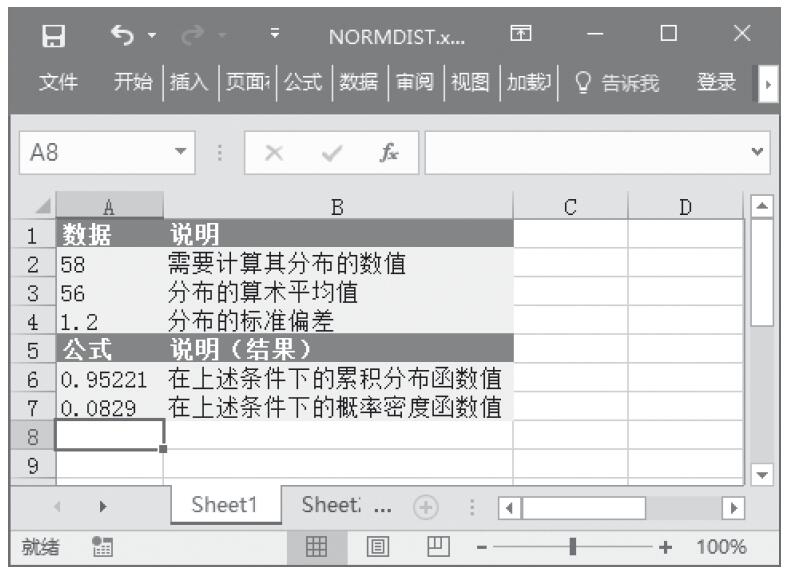
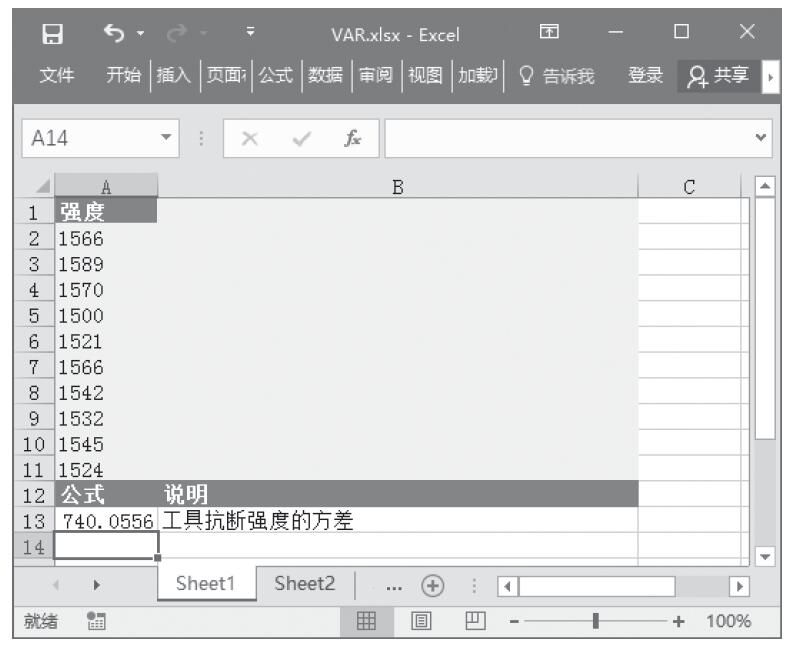
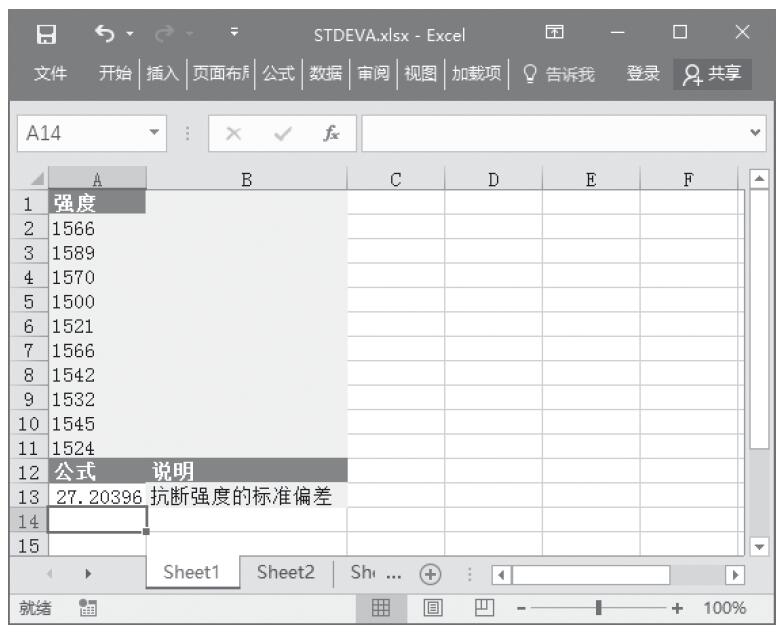
步骤3：在单元格A7中输入公式“=NORMDIST（A2，A3，A4，FALSE）”，用于计算在上述条件下的概率密度函数值。计算结果如图16-104所示。
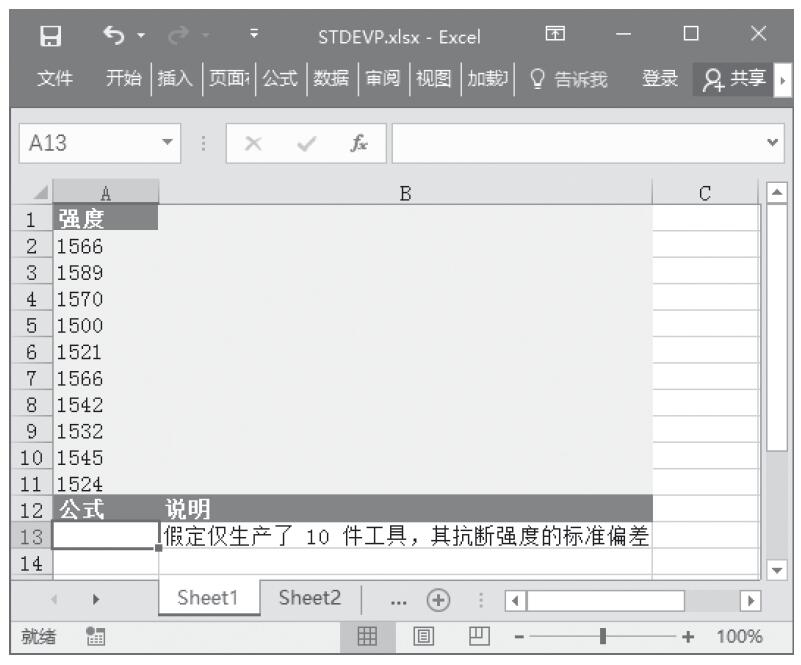
图16-103 基础数据
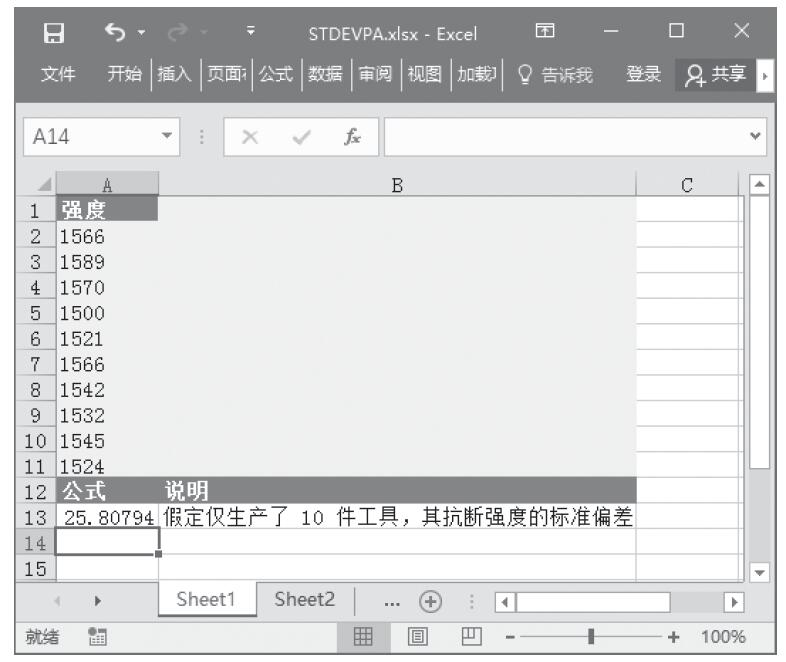
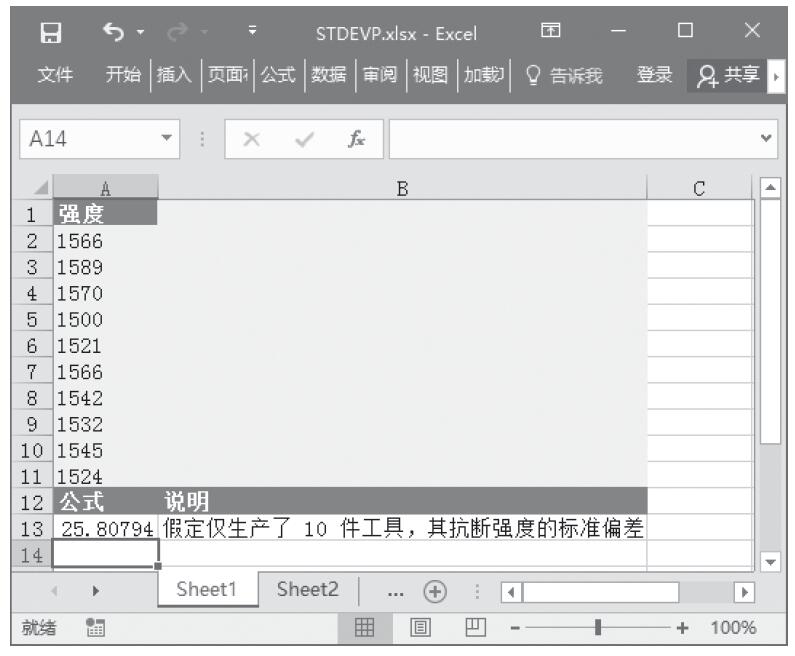
图16-104 计算结果
如果mean或standard_dev为非数值型，函数NORMDIST返回错误值“#VALUE！”。如果standard_dev≤0，函数NORMDIST返回错误值“#NUM！”。如果mean=0，standard_dev=1，且cumulative=TRUE，则函数NORMDIST返回标准正态分布，即函数NORMSDIST。正态分布密度函数（cumulative=FALSE）的计算公式如下。
如果cumulative=TRUE，则公式为从负无穷大到公式中给定的X的积分。
VARP函数用于计算基于样本总体的方差。VARP函数的语法如下。
VARP(number1,number2,...)
其中参数number1，number2，…为对应于样本总体的1到255个参数。
假定某工厂仅生产了10种产品，取样为随机样本进行抗断强度检验。基础数据如图16-101所示。
步骤1：打开例子工作簿“VARP.xlsx”。
步骤2：在单元格A13中输入公式“=VARP（A2：A11）”，用于计算全部工具抗断强度的方差（假定仅生产了10件工具）。计算结果如图16-102所示。
图16-101 基础数据
图16-102 计算结果
函数VARP假设其参数为样本总体。如果数据只是代表样本总体中的一个样本，则使用函数VAR计算方差。参数可以是数字或者是包含数字的名称、数组或引用。逻辑值和直接键入到参数列表中代表数字的文本被计算在内。
如果参数是一个数组或引用，则只计算其中的数字，数组或引用中的空白单元格、逻辑值、文本或错误值将被忽略。如果参数为错误值或为不能转换为数字的文本，将会导致错误；如果要使计算包含引用中的逻辑值和代表数字的文本，则需要使用VARPA函数。函数VARP的计算公式如下：
其中x为样本平均值AVERAGE（number1，number2，…），n为样本大小。
VARA函数用于计算基于给定样本的方差。VARA函数的语法如下。
VARA(value1,value2,...)
其中参数value1，value2，…为对应于总体的一个样本的1到255个数值参数。
假定某工厂仅生产了10种产品，取样为随机样本进行抗断强度检验。基础数据如图16-99所示。
步骤1：打开例子工作簿“VARA.xlsx”。
步骤2：在单元格A13中输入公式“=VARA（A2：A11）”，用于计算工具抗断强度的方差。计算结果如图16-100所示。
图16-99 基础数据
图16-100 计算结果
函数VARA假设其参数为总体的一个样本。如果数据代表的是样本总体，则必须使用函数VARPA来计算方差。参数可以是下列形式：数值；包含数值的名称、数组或引用；数字的文本表示；或者引用中的逻辑值，如TRUE和FALSE。逻辑值和直接键入到参数列表中代表数字的文本被计算在内。
包含TRUE的参数作为1来计算，包含文本或FALSE的参数作为0（零）来计算，如果参数为数组或引用，则只使用其中的数值，数组或引用中的空白单元格和文本值将被忽略；如果参数为错误值或为不能转换为数字的文本，将会导致错误；如果要使计算不包括引用中的逻辑值和代表数字的文本，则需要使用VAR函数。函数VARA的计算公式如下。
其中x是样本平均值AVERAGE（value1，value2，…）且n是样本大小。
VAR函数用于计算基于给定样本的方差。VAR函数的语法如下。
VAR(number1,number2,...)
其中参数number1，number2，…为对应于总体样本的1到255个参数。
假定某工厂仅生产了10种产品，取样为随机样本进行抗断强度检验。基础数据如图16-97所示。
步骤1：打开例子工作簿“VAR.xlsx”。
步骤2：在单元格A13中输入公式“=VAR（A2：A11）”，用于计算工具抗断强度的方差。计算结果如图16-98所示。
图16-97 基础数据
图16-98 计算结果
函数VAR假设其参数是样本总体中的一个样本。如果数据为整个样本总体，则应使用函数VARP来计算方差。参数可以是数字或者是包含数字的名称、数组或引用。逻辑值和直接键入到参数列表中代表数字的文本被计算在内。
如果参数是一个数组或引用，则只计算其中的数字，数组或引用中的空白单元格、逻辑值、文本或错误值将被忽略。如果参数为错误值或为不能转换为数字的文本，将会导致错误；如果要使计算包含引用中的逻辑值和代表数字的文本，则需要使用VARA函数。函数VAR的计算公式如下。
其中x为样本平均值AVERAGE（number1，number2，…），n为样本大小。
VARPA函数用于计算基于样本总体的方差。VARPA函数的语法如下。
VARPA(value1,value2,...)
其中参数value1，value2，…为对应于样本总体的1到255个参数。
假定某工厂仅生产了10种产品，取样为随机样本进行抗断强度检验。基础数据如图16-95所示。
步骤1：打开例子工作簿“VARPA.xlsx”。
步骤2：在单元格A13中输入公式“=VARPA（A2：A11）”，用于计算全部工具抗断强度的方差（假定仅生产了10件工具）。计算结果如图16-96所示。
图16-95 基础数据
图16-96 计算结果
函数VARPA假设其参数为样本总体。如果数据代表的是总体的一个样本，则必须使用函数VARA来计算方差。参数可以是下列形式：数值；包含数值的名称、数组或引用；数字的文本表示；或者引用中的逻辑值，例如TRUE和FALSE。逻辑值和直接键入到参数列表中代表数字的文本被计算在内。包含TRUE的参数作为1来计算，包含文本或FALSE的参数作为0（零）来计算。
如果参数为数组或引用，则只使用其中的数值，数组或引用中的空白单元格和文本值将被忽略；如果参数为错误值或为不能转换为数字的文本，将会导致错误；如果要使计算不包括引用中的逻辑值和代表数字的文本，则需要使用VAR函数。函数VARPA的计算公式如下。
其中x是样本平均值AVERAGE（value1，value2，…）且n是样本大小。
STDEVPA函数用于以参数形式给出的样本总体的标准偏差，包含文本和逻辑值。标准偏差反映数值相对于平均值（mean）的离散程度。STDEVPA函数的语法如下。
STDEVPA(value1,value2,...)
其中参数value1，value2，…作为样本总体的1到255个参数。也可以不使用这种用逗号分隔参数的形式，而用单个数组或对数组的引用。
假定某工厂仅生产了10种产品，取样为随机样本进行抗断强度检验。基础数据如图16-93所示。
步骤1：打开例子工作簿“STDEVPA.xlsx”。
步骤2：在单元格A13中输入公式“=STDEVPA（A2：A11）”，用于计算基于总体的抗断强度的标准偏差。计算结果如图16-94所示。
图16-93 基础数据
图16-94 计算结果
函数STDEVPA假设其参数为样本总体。如果数据代表的是总体的一个样本，则必须使用函数STDEVA来计算标准偏差。对于大样本容量，函数STDEVA和函数STDEVPA的返回值大致相等。此处标准偏差的计算使用“n”方法。参数可以是下列形式：数值；包含数值的名称、数组或引用；数字的文本表示；或者引用中的逻辑值，例如TRUE和FALSE。直接键入到参数列表中代表数字的文本被计算在内。
包含TRUE的参数作为1来计算，包含文本或FALSE的参数作为0（零）来计算。如果参数为数组或引用，则只使用其中的数值，数组或引用中的空白单元格和文本值将被忽略；如果参数为错误值或为不能转换成数字的文本，将会导致错误；如果要使计算不包括引用中的逻辑值和代表数字的文本，则需要使用STDEVP函数。函数STDEVPA的计算公式如下。
其中x是样本平均值AVERAGE（value1，value2，…）且n是样本大小。
STDEVP函数用于计算以参数形式给出的样本总体的标准偏差。标准偏差反映数值相对于平均值（mean）的离散程度。STDEVP函数的语法如下。
STDEVP(number1,number2,...)
其中参数number1，number2，…为对应于样本总体的1到255个参数。也可以不使用这种用逗号分隔参数的形式，而用单个数组或对数组的引用。
假定某工厂仅生产了10种产品，取样为随机样本进行抗断强度检验。基础数据如图16-91所示。
步骤1：打开例子工作簿“STDEVP.xlsx”。
步骤2：在单元格A13中输入公式“=STDEVP（A2：A11）”，用于计算基于整个样本总体的抗断强度的标准偏差。计算结果如图16-92所示。
图16-91 基础数据
图16-92 计算结果
函数STDEVP假设其参数为整个样本总体。如果数据代表样本总体中的样本，应使用函数STDEV来计算标准偏差。对于大样本容量，函数STDEV和STDEVP计算结果大致相等。此处标准偏差的计算使用“n”方法。参数可以是数字或者是包含数字的名称、数组或引用。逻辑值和直接键入到参数列表中代表数字的文本被计算在内。
如果参数是一个数组或引用，则只计算其中的数字，数组或引用中的空白单元格、逻辑值、文本或错误值将被忽略；如果参数为错误值或为不能转换成数字的文本，将会导致错误；如果要使计算包含引用中的逻辑值和代表数字的文本，则需要使用STDEVPA函数。函数STDEVP的计算公式如下。
其中x为样本平均值AVERAGE（number1，number2，…），n为样本大小。
STDEVA函数用于计算基于样本的估算标准偏差。标准偏差反映数值相对于平均值（mean）的离散程度。STDEVA函数的语法如下。
STDEVA(value1,value2,...)
其中参数value1，value2，…作为总体的一个样本的1到255个参数。也可以不使用这种用逗号分隔参数的形式，而用单个数组或对数组的引用。
某工厂有10种产品在制造过程中是由同一台机器制造出来的，并取样为随机样本进行抗断强度检验。基础数据如图16-89所示。
步骤1：打开例子工作簿“STDEVA.xlsx”。
步骤2：在单元格A13中输入公式“=STDEVA（A2：A11）”，用于计算基于样本（包括数字、文本和逻辑值）的抗断强度的估算标准偏差。计算结果如图16-90所示。
图16-89 基础数据
图16-90 计算结果
函数STDEVA假设参数为总体的一个样本。如果数据代表的是样本总体，则必须使用函数STDEVPA来计算标准偏差。此处标准偏差的计算使用“n-1”方法。参数可以是下列形式：数值；包含数值的名称、数组或引用；数字的文本表示；或者引用中的逻辑值，例如TRUE和FALSE。包含TRUE的参数作为1来计算，包含文本或FALSE的参数作为0（零）来计算。如果参数为数组或引用，则只使用其中的数值，数组或引用中的空白单元格和文本值将被忽略；如果参数为错误值或为不能转换成数字的文本，将会导致错误；如果要使计算不包括引用中的逻辑值和代表数字的文本，则需要使用STDEV函数。函数STDEVA的计算公式如下。
其中x是样本平均值AVERAGE（value1，value2，…）且n是样本大小。