分类：统计函数应用技巧

Excel中的统计函数主要用于对数据区域进行各种分类统计与分析。统计函数包括了许多统计学领域的函数，具体包括平均值函数、Beta分布函数、概率函数、单元格数量计算函数、指数与对数函数、最大值与最小值函数、标准偏差函数、方差函数、正态累积分布函数、数据集相关函数、Pearson乘积矩函数、t分布函数等。本章将通过实例介绍统计函数的基本语法、参数用法以及在实际中的应用。

Excel 应用CHITEST函数计算独立性检验值

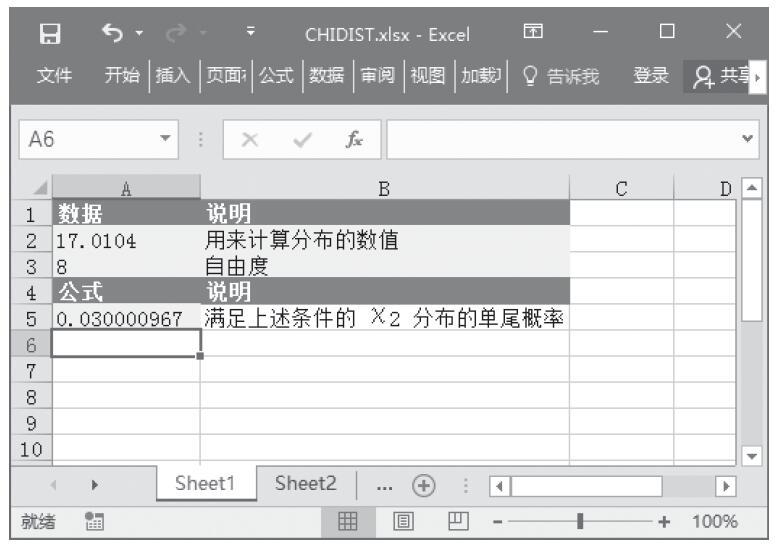
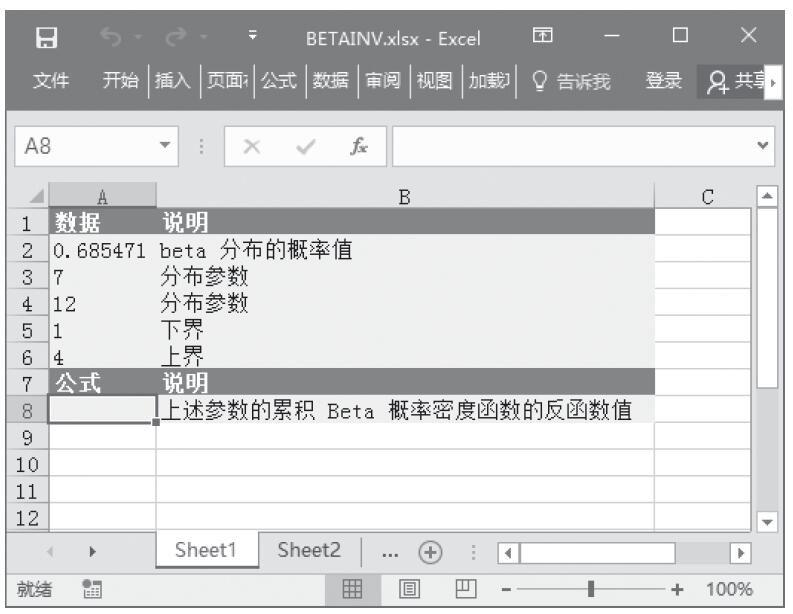
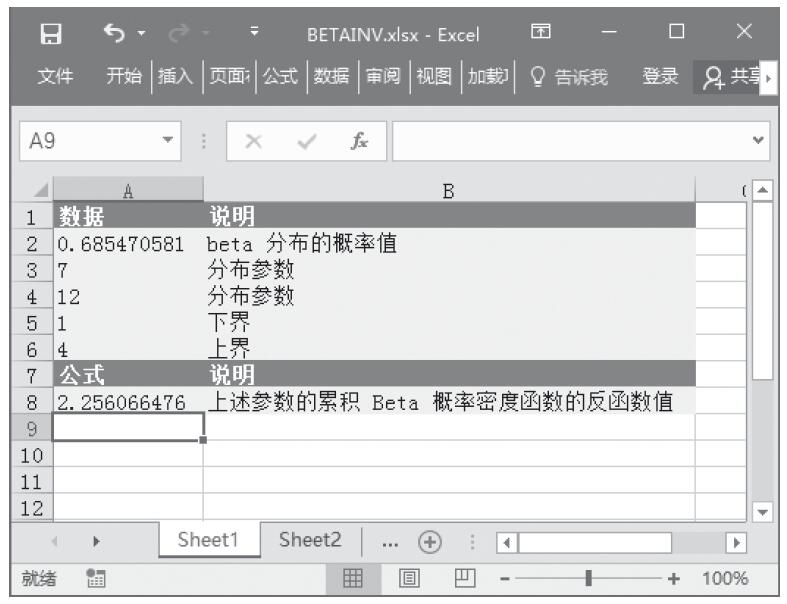
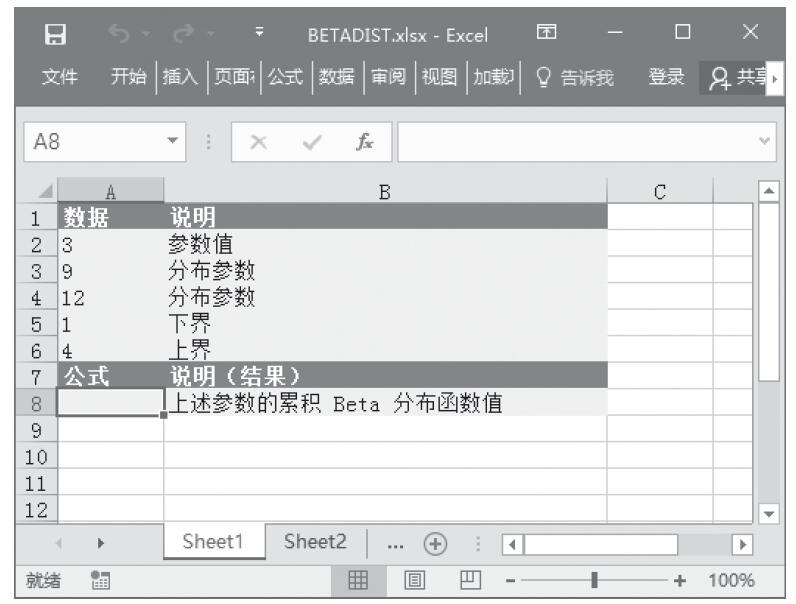
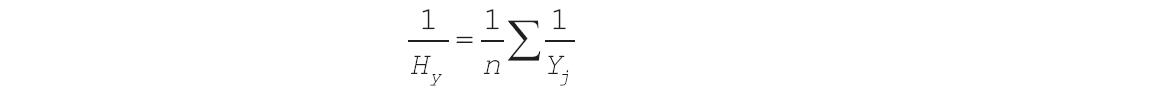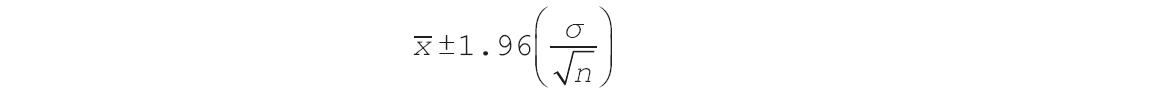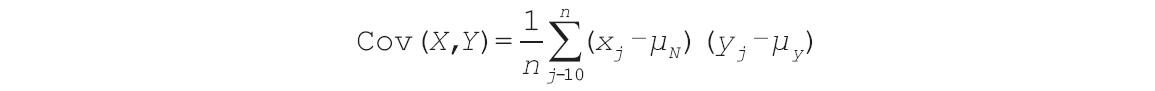CHITEST函数用于计算独立性检验值。函数CHITEST返回（χ2）分布的统计值及相应的自由度。可以使用（χ2）检验值确定假设值是否被实验所证实。CHITEST函数的语法如下。

CHITEST(actual_range,expected_range)

其中参数actual_range为包含观察值的数据区域，将对期望值作检验。expected_range为包含行列汇总的乘积与总计值之比率的数据区域。

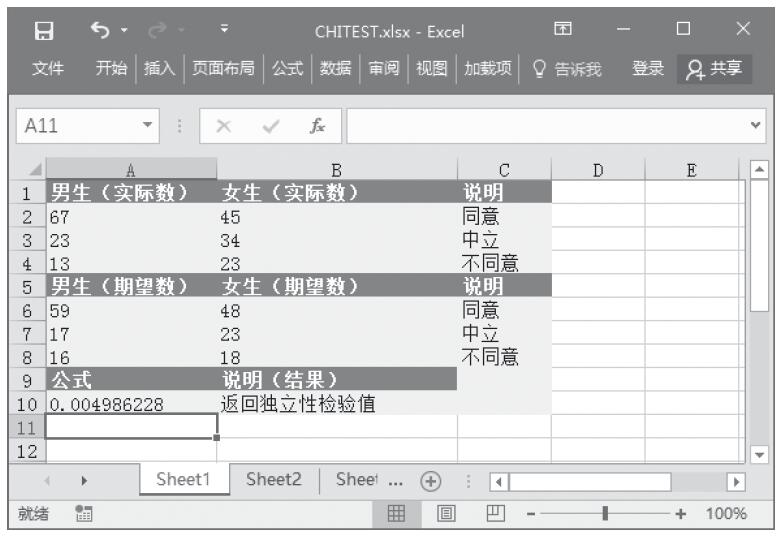
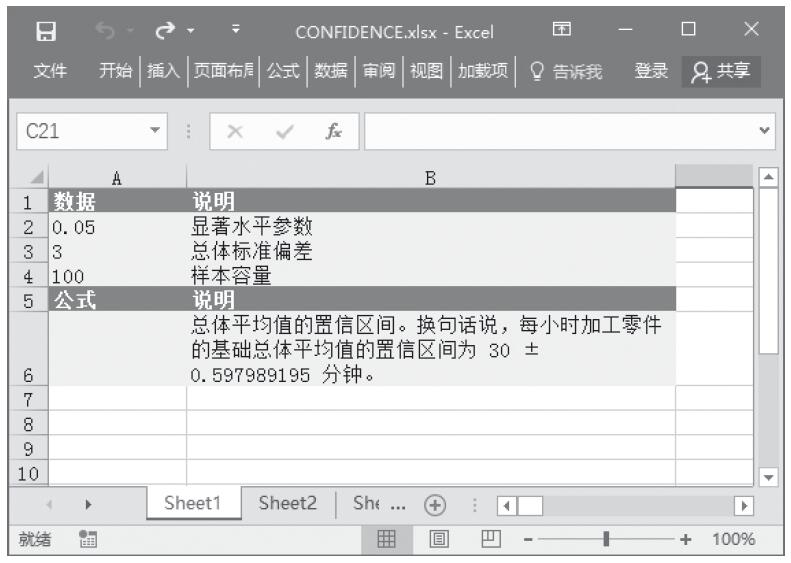
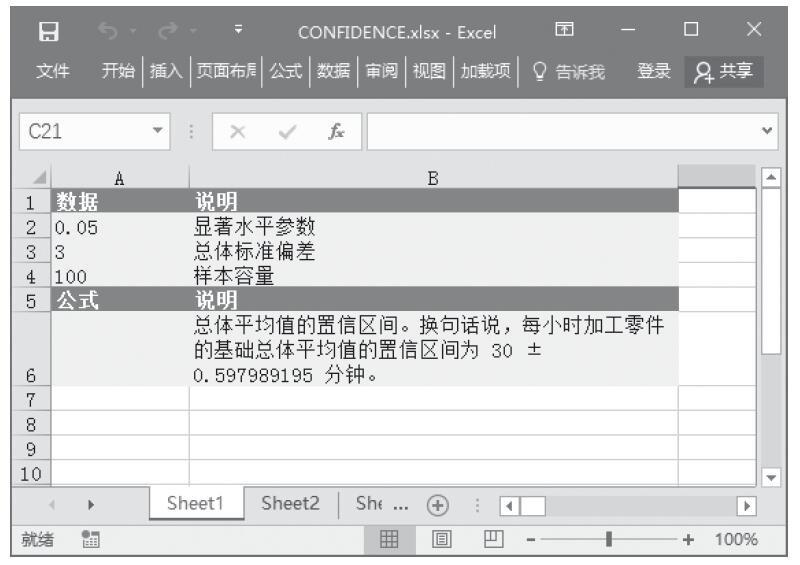
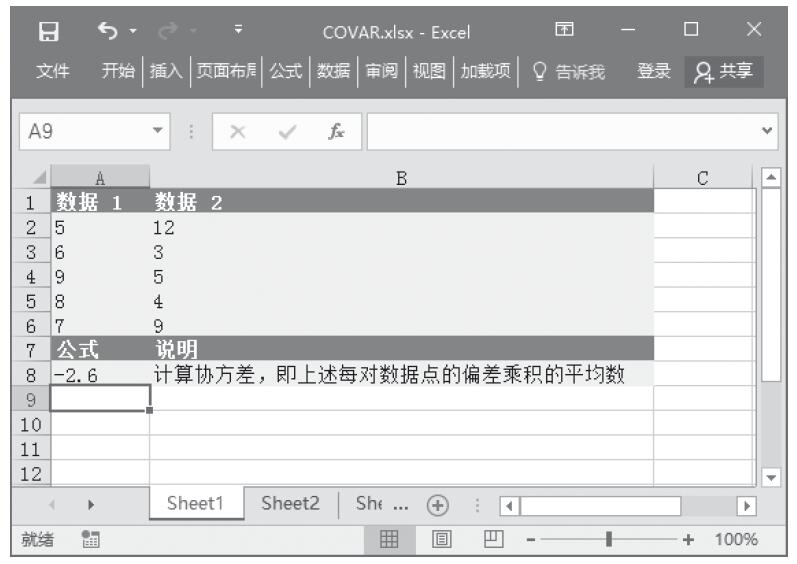
【典型案例】某班统计本班中男生与女生去某地旅游的意向，已知统计的实际数值与期望数值，计算相关性检验值。基础数据如图16-27所示。

步骤1：打开例子工作簿“CHITEST.xlsx”。

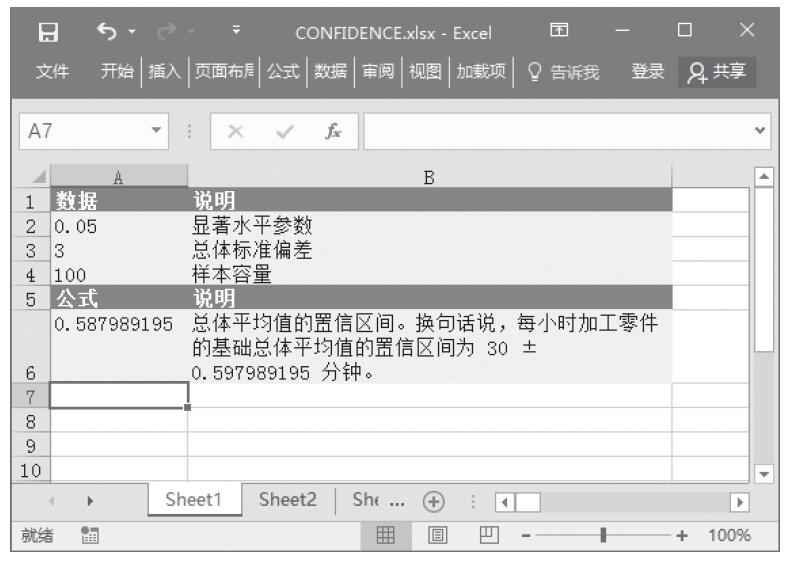
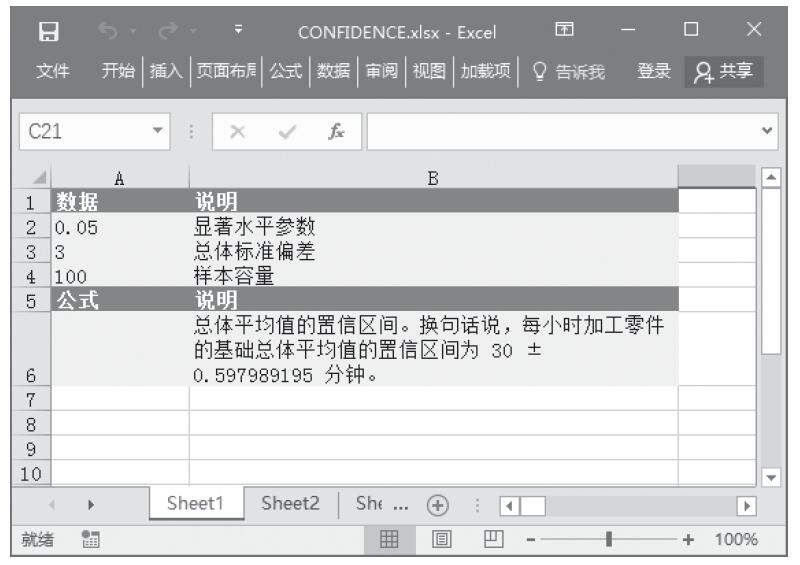
步骤2：在单元格A10中输入公式“=CHITEST（A2：B4，A6：B8）”，用于计算总体平均值的置信区间。计算结果如图16-28所示。

【使用指南】1）如果actual_range和expected_range数据点的个数不同，则函数CHITEST返回错误值“#N/A”。χ2检验首先使用下面的公式计算χ2统计：

检验

式中：

Aij为第i行、第j列的实际频率。

Eij为第i行、第j列的期望频率。

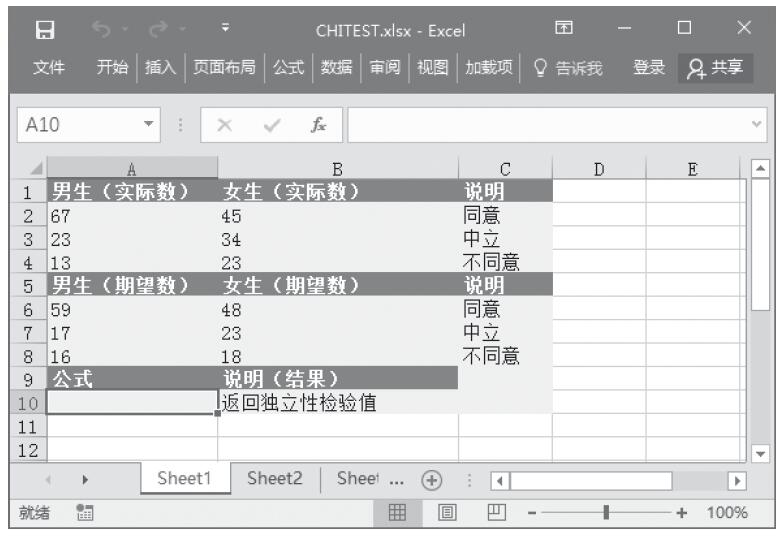
图16-27　基础数据

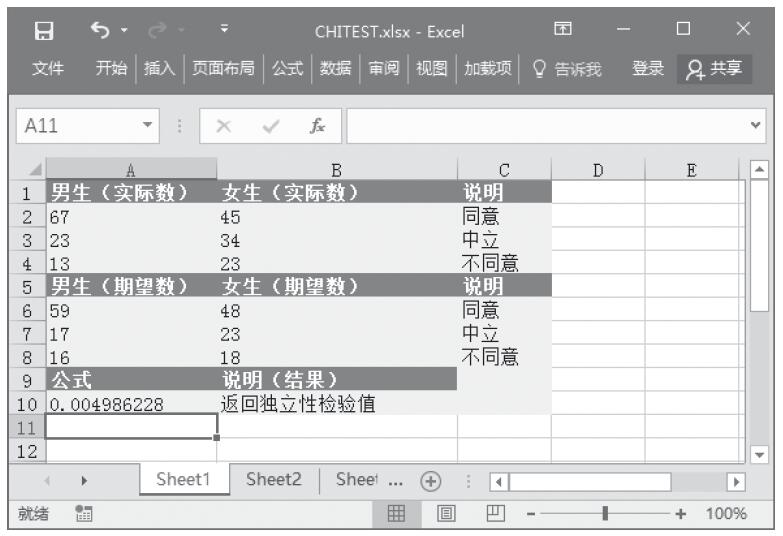
图16-28　计算结果

2）从公式中可看出，χ2总是正数或0，且为0的条件是：对于每个i和j，如果Aij=Eij。

3）CHITEST返回在独立的假设条件下意外获得特定情况的概率，即χ2统计值至少与由上面的公式计算出的值一样大的情况。在计算此概率时，CHITEST使用具有相应自由度df的个数的χ2分布。如果r＞1且c＞1，则df=（r-1）（c-1）。如果r=1且c＞1，则df=c-1。或者如果r＞1且c=1，则df=r-1。不允许出现r=c=1并且返回“#N/A”。

4）当Eij的值不太小时，使用CHITEST最合适。某些统计人员建议每个Eij应该大于等于5。

Excel 应用CHIINV函数计算χ2分布的单尾概率的反函数

CHIINV函数用于返回χ2分布单尾概率的反函数值。如果probability=CHIDIST（x，…），则CHIINV（probability，…）=x。使用此函数可比较观测结果和期望值，可确定初始假设是否有效。CHIINV函数的语法如下。

CHIINV(probability,degrees_freedom)

其中参数probability为与χ2分布相关的概率，degrees_freedom为自由度的数值。

【典型案例】给定用来计算分布的数值和自由度，计算χ2分布的单尾概率的反函数。基础数据如图16-25所示。

步骤1：打开例子工作簿“CHIINV.xlsx”。

步骤2：在单元格A5中输入公式“=CHIINV（A2，A3）”，用于计算χ2分布的单尾概率的反函数。计算结果如图16-26所示。

图16-25　基础数据

图16-26　计算结果

【使用指南】如果任一参数为非数字型，则函数CHIINV返回错误值“#VALUE！”。如果probability＜0或probability＞1，则函数CHIINV返回错误值“#NUM！”。如果degrees_freedom不是整数，将被截尾取整。如果degrees_freedom＜1或degrees_freedom≥1010，函数CHIINV返回错误值“#NUM！”。如果已给定概率值，则CHIINV使用CHIDIST（x，degrees_freedom）=probability求解数值x。因此，CHIINV的精度取决于CHIDIST的精度。CHIINV使用迭代搜索技术，如果搜索在100次迭代之后没有收敛，则函数返回错误值“#N/A”。

Excel 应用CHIDIST函数计算χ2分布的单尾概率

CHIDIST函数用于返回χ2分布的单尾概率。χ2分布与χ2检验相关。使用χ2检验可以比较观察值和期望值。例如，某项遗传学实验假设下一代植物将呈现出某一组颜色。使用此函数比较观测结果和期望值，可以确定初始假设是否有效。CHIDIST函数的语法如下。

CHIDIST(x,degrees_freedom)

其中参数x为用来计算分布的数值。degrees_freedom为自由度的数值。

【典型案例】给定用来计算分布的数值和自由度，计算χ2分布的单尾概率。基础数据如图16-23所示。

步骤1：打开例子工作簿“CHIDIST.xlsx”。

步骤2：在单元格A5中输入公式“=CHIDIST（A2，A3）”，用于计算χ2分布的单尾概率。计算结果如图16-24所示。

图16-23　基础数据

图16-24　计算结果

【使用指南】如果任一参数为非数值型，函数CHIDIST返回错误值“#VALUE！”。如果x为负数，函数CHIDIST返回错误值“#NUM！”。如果degrees_freedom不是整数，将被截尾取整。如果degrees_freedom＜1或degrees_freedom＞1010，则函数CHIDIST返回错误值“#NUM！”。函数CHIDIST按CHIDIST=P（X＞x）计算，式中X为χ2随机变量。

Excel 应用BETAINV函数计算指定Beta分布的累积分布函数的反函数

BETAINV函数用于返回指定的Beta分布累积Beta分布的概率密度函数的反函数值。即，如果probability=BETADIST（x，…），则BETAINV（probability，…）=x。Beta分布函数可用于项目设计，在给定期望的完成时间和变化参数后，模拟可能的完成时间。BETAINV函数的语法如下。

BETAINV(probability,alpha,beta,A,B)

其中参数probability为Beta分布的概率值。alpha与beta为分布参数。A为数值x所属区间的可选下界，B为数值x所属区间的可选上界。

【典型案例】已知Beta分布的相关参数，返回指定Beta分布的累积分布函数的反函数。基础数据如图16-21所示。

步骤1：打开例子工作簿“BETAINV.xlsx”。

步骤2：在单元格A8中输入公式“=BETAINV（A2，A3，A4，A5，A6）”，用于计算指定Beta分布的累积分布函数的反函数。计算结果如图16-22所示。

图16-21　基础数据

图16-22　计算结果

【使用指南】如果任意参数为非数值型，函数BETAINV返回错误值“#VALUE！”；如果alpha≤0或beta≤0，函数BETAINV返回错误值“#NUM！”；如果probability≤0或probability＞1，函数BETAINV返回错误值“#NUM！”。如果省略A或B值，函数BETAINV使用标准的累积Beta分布，即A=0，B=1。如果已给定概率值，则BETAINV使用BETADIST（x，alpha，beta，A，B）=probability求解数值x。因此，BETAINV的精度取决于BETADIST的精度。BETAINV使用迭代搜索技术，如果搜索在100次迭代之后没有收敛，则函数返回错误值“#N/A”。

Excel 应用BETADIST函数计算Beta累积分布函数

BETADIST函数返回累积Beta分布的概率密度函数。累积Beta分布函数通常用于研究样本中一定部分的变化情况。例如，人们一天中看电视的时间比率。BETADIST函数的语法如下。

BETADIST(x,alpha,beta,A,B)

其中参数x为用来进行函数计算的值，居于可选性上下界（A和B）之间。alpha与beta为分布参数。A为数值x所属区间的可选下界，B为数值x所属区间的可选上界。

【典型案例】已知Beta分布的相关参数，计算Beta累积分布的函数。基础数据如图16-19所示。

步骤1：打开例子工作簿“BETADIST.xlsx”。

步骤2：在单元格A8中输入公式“=BETADIST（A2，A3，A4，A5，A6）”，用于计算Beta累积分布的函数。计算结果如图16-20所示。

图16-19　基础数据

图16-20　计算结果

【使用指南】如果任意参数为非数值型，函数BETADIST返回错误值“#VALUE！”。如果alpha≤0或beta≤0，函数BETADIST返回错误值“#NUM！”。如果x＜A、x＞B或A=B，函数BETADIST返回错误值“#NUM！”。如果省略A或B值，函数BETADIST使用标准Beta分布的累积函数，即A=0，B=1。

Excel 应用HARMEAN函数计算调和平均值

HARMEAN函数返回数据集合的调和平均值。调和平均值与倒数的算术平均值互为倒数。HARMEAN函数的语法如下。

HARMEAN(number1,number2,...)

其中参数number1，number2，…是用于计算平均值的1到255个参数，也可以不用这种用逗号分隔参数的形式，而用单个数组或对数组的引用。

【典型案例】已知一组原始数据，计算该组数据的调和平均值。基础数据如图16-17所示。

步骤1：打开例子工作簿“HARMEAN.xlsx”。

步骤2：在单元格A10中输入公式“=HARMEAN（A2：A8）”，用于计算数据集的调和平均值。计算结果如图16-18所示。

图16-17　基础数据

图16-18　计算结果

【使用指南】调和平均值总小于几何平均值，而几何平均值总小于算术平均值。参数可以是数字或者是包含数字的名称、数组或引用。逻辑值和直接键入到参数列表中代表数字的文本被计算在内。如果数组或引用参数包含文本、逻辑值或空白单元格，则这些值将被忽略，但包含零值的单元格将计算在内。如果参数为错误值或为不能转换为数字的文本，将会导致错误。如果任何数据点小于等于0，函数HARMEAN返回错误值“#NUM！”。调和平均值的计算公式如下。

Excel 应用GEOMEAN函数计算几何平均值

GEOMEAN函数用于计算正数数组或区域的几何平均值。例如，可以使用函数GEOMEAN计算可变复利的平均增长率。GEOMEAN函数的语法如下。

GEOMEAN(number1,number2,...)

其中参数number1，number2，…是用于计算平均值的1到255个参数，也可以不用这种用逗号分隔参数的形式，而用单个数组或对数组的引用。

【典型案例】计算一个数据集的几何平均值。基础数据如图16-15所示。

步骤1：打开例子工作簿“GEOMEAN.xlsx”。

步骤2：在单元格A10中输入公式“=GEOMEAN（A2：A8）”，用于计算数据集的几何平均值。计算结果如图16-16所示。

【使用指南】参数可以是数字或者是包含数字的名称、数组或引用。逻辑值和直接键入到参数列表中代表数字的文本被计算在内。如果数组或引用参数包含文本、逻辑值或空白单元格，则这些值将被忽略；但包含零值的单元格将计算在内。如果参数为错误值或为不能转换为数字的文本，将会导致错误。如果任何数据点小于0，函数GEOMEAN返回错误值“#NUM！”。几何平均值的计算公式如下。

图16-15　基础数据

图16-16　计算结果

Excel 应用CONFIDENCE函数计算总体平均值的置信区间

CONFIDENCE函数可以返回一个值，可以使用该值构建总体平均值的置信区间。CONFIDENCE函数的语法如下。

CONFIDENCE(alpha,standard_dev,size)

其中参数alpha是用于计算置信度的显著水平参数。置信度等于100×（1-alpha）%，也就是说，如果alpha为0.05，则置信度为95%。standard_dev为数据区域的总体标准偏差，假设为已知。size为样本容量。

【背景知识】置信区间是一个值区域。样本平均值x位于该区域的中间，区域范围为x±CONFIDENCE。例如，如果通过邮购的方式定购产品，其交付时间的样本平均值为x，则总体平均值的区域范围为x±CONFIDENCE。对于任何包含在本区域中的总体平均值μ0，从μ0到x，获取样本平均值的概率大于alpha；对于任何未包含在本区域中的总体平均值μ0，从μ0到x，获取样本平均值的概率小于alpha。换句话说，假设使用x、standard_dev和size构建一个双尾检验，假设的显著性水平为alpha，总体平均值为μ0。如果μ0包含在置信区间中，则不能拒绝该假设；如果μ0未包含在置信区间中，则将拒绝该假设。置信区间不允许进行概率为1–alpha的推断，此时下一份包裹的交付时间将肯定位于置信区间内。

【典型案例】假设样本取自100名某生产车间的工人，他们平均每小时加工的零件数量为20个，总体标准偏差为3个。假设alpha=0.05，计算CONFIDENCE（.05，3，100）的返回值为0.692952。那么，相应的置信区间为20±0.692952≈[19.3，20.7]。对于包含在本区间中的任何总体平均值μ0，从μ0到30，获取样本平均值的概率大于0.05。同样地，对于未包含在本区间中的任何总体平均值μ0，从μ0到30，获取样本平均值的概率小于0.05。基础数据如图16-13所示。

步骤1：打开例子工作簿“CONFIDENCE.xlsx”。

步骤2：在单元格A6中输入公式“=CONFIDENCE（.05，3，100）”，用于计算总体平均值的置信区间。计算结果如图16-14所示。

图16-13　基础数据

图16-14　计算结果

【使用指南】如果任意参数为非数值型，函数CONFIDENCE返回错误值“#VALUE！”。如果alpha≤0或alpha≥1，函数CONFIDENCE返回错误值“#NUM！”。如果standard_dev≤0，函数CONFIDENCE返回错误值“#NUM！”。如果size不是整数，将被截尾取整。如果size＜1，函数CONFIDENCE返回错误值“#NUM！”。如果假设alpha等于0.05，则需要计算等于（1-alpha）或95%的标准正态分布曲线之下的面积，其面积值为±1.96。此时置信区间为：

应用COVAR函数计算协方差

COVAR函数用来计算协方差，即每对数据点的偏差乘积的平均数，利用协方差可以决定两个数据集之间的关系。例如，可利用它来检验教育程度与收入档次之间的关系。COVAR函数的语法如下。

COVAR(array1,array2)

其中参数array1为第一个所含数据为整数的单元格区域，array2为第二个所含数据为整数的单元格区域。

【背景知识】协方差计算公式为：

其中x和y是样本平均值AVERAGE（array1）和AVERAGE（array2），且n是样本大小。

【典型案例】某工厂统计了不同加工条件（数据1）下设备的成品数量（数据2），需要计算两组数据的协方差。基础数据如图16-11所示。

步骤1：打开例子工作簿“COVAR.xlsx”。

步骤2：在单元格A8中输入公式“=COVAR（A2：A6，B2：B6）”，用于计算协方差，即上述每对数据点的偏差乘积的平均数。计算结果如图16-12所示。

图16-11　原始数据

图16-12　计算结果

【使用指南】参数必须是数字，或者是包含数字的名称、数组或引用。如果数组或引用参数包含文本、逻辑值或空白单元格，则这些值将被忽略，但包含零值的单元格将计算在内。如果array1和array2所含数据点的个数不等，则函数COVAR返回错误值“#N/A”。如果array1和array2当中有一个为空，则函数COVAR返回错误值“#DIV/0！”。

应用AVERAGEIFS函数计算满足多重条件的平均值

AVERAGEIFS函数用于返回满足多重条件的所有单元格的平均值（算术平均值）。其语法如下。

AVERAGEIFS(average_range,criteria_range1,criteria1,criteria_range2,criteria2…)

其中参数average_range是要计算平均值的一个或多个单元格，其中包括数字或包含数字的名称、数组或引用。criteria_range1，criteria_range2，…是计算关联条件的1至127个区域。criteria1，criteria2，…是数字、表达式、单元格引用或文本形式的1至127个条件，用于定义要对哪些单元格求平均值。

【典型案例】某房产公司统计了两个不同地区不同户型房屋的售价，需要计算满足多重条件的房屋售价的平均值。基础数据如图16-9所示。

步骤1：打开例子工作簿“AVERAGEIFS.xlsx”。

步骤2：在单元格A9中输入公式“=AVERAGEIFS（B2：B7，C2：C7，”烟台”，D2：D7，”>2″，E2：E7，”是”）”，用于计算烟台市一个至少有3间卧室和一个车库的住房价格的平均值。

步骤3：在单元格A10中输入公式“=AVERAGEIFS（B2：B7，C2：C7，”威海”，D2：D7，”<=3″，E2：E7，”否”）”，用于计算威海市一个最多有3间卧室但没有车库的住房价格的平均值。计算结果如图16-10所示。

图16-9　基础数据

图16-10　计算结果