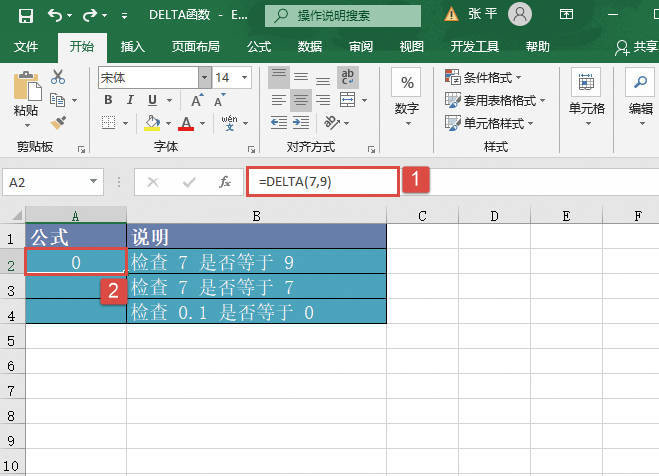
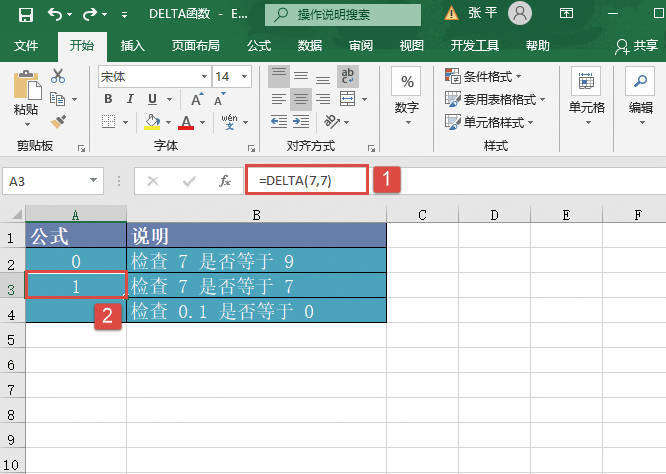
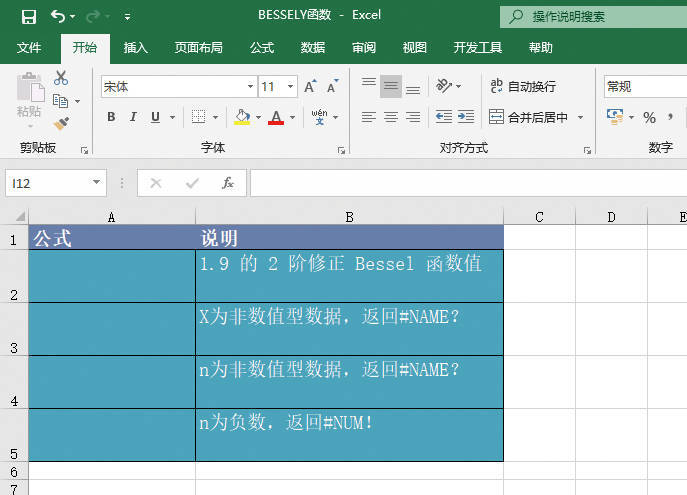
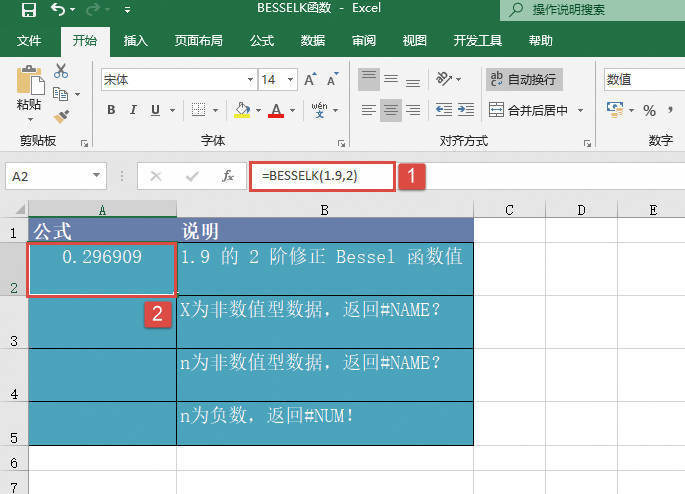
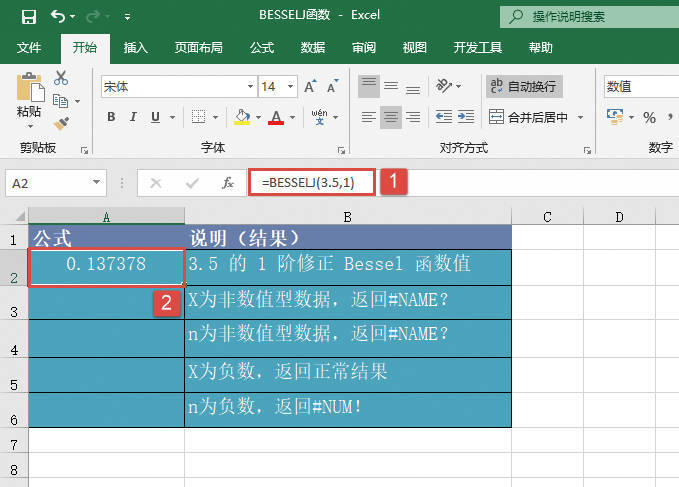
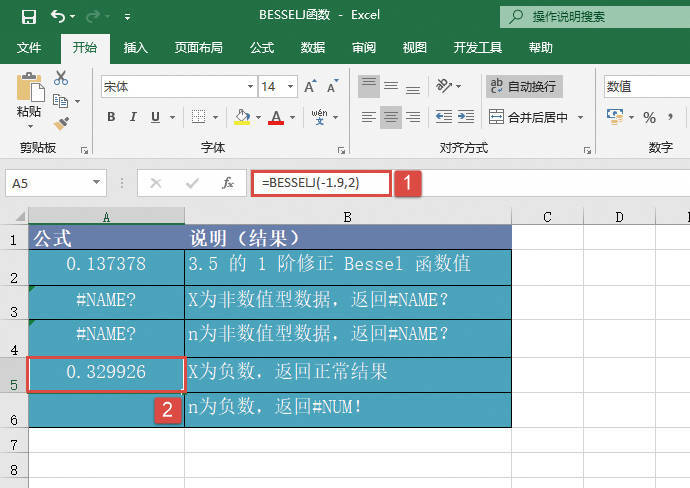
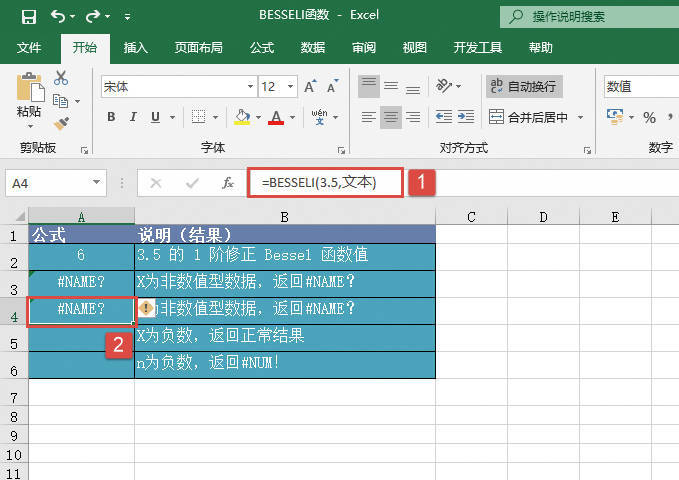
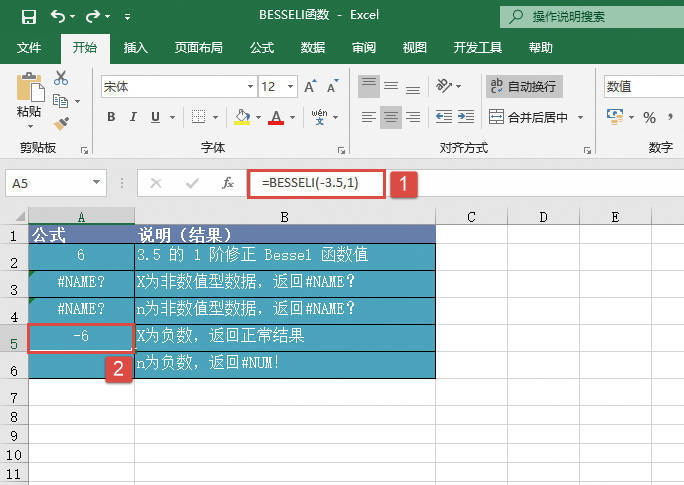
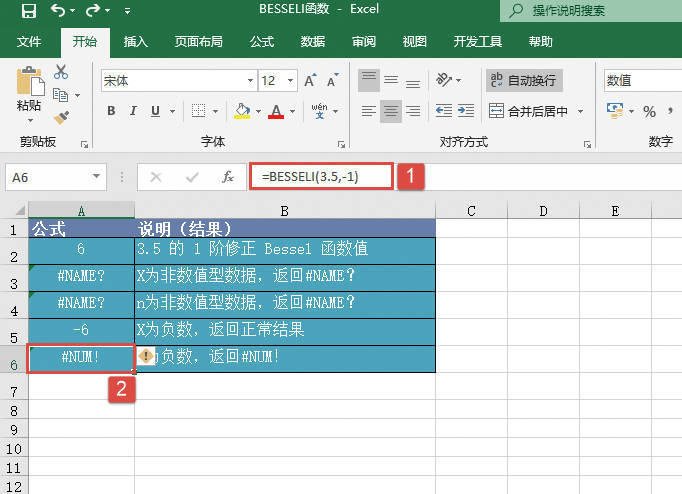
GESTEP函数用于检验数字是否大于阈值。如果number大于等于step,返回1,否则返回0。使用该函数可筛选数据。例如,通过计算多个函数GESTEP的返回值,可以检测出数据集中超过某个临界值的数据个数。GESTEP函数的语法如下:
GESTEP(number,step)
其中,number参数为待测试的数值,step参数为阈值。如果省略step参数,则函数GESTEP假设其为零。下面通过实例详细讲解该函数的使用方法与技巧。
打开“GESTEP函数.xlsx”工作簿,切换至“Sheet1”工作表,本例的数据说明如图20-88所示。要求在工作表中检查数字是否大于阈值。具体的操作步骤如下。

图20-88 原始数据
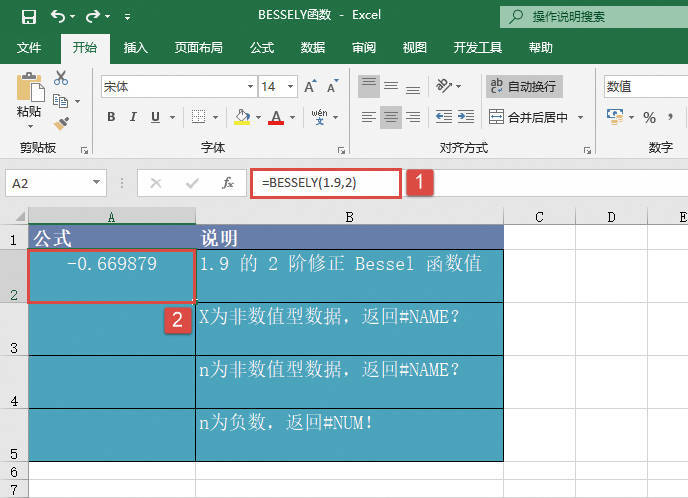
STEP01:选中A2单元格,在编辑栏中输入公式“=GESTEP(8,7)”,然后按“Enter”键返回,此时工作表结果显示为“1”,即检查出8满足大于等于7的条件,如图20-89所示。
STEP02:选中A3单元格,在编辑栏中输入公式“=GESTEP(8,8)”,然后按“Enter”键返回,此时工作表结果显示为“1”,即检查出8满足大于等于8的条件,如图20-90所示。
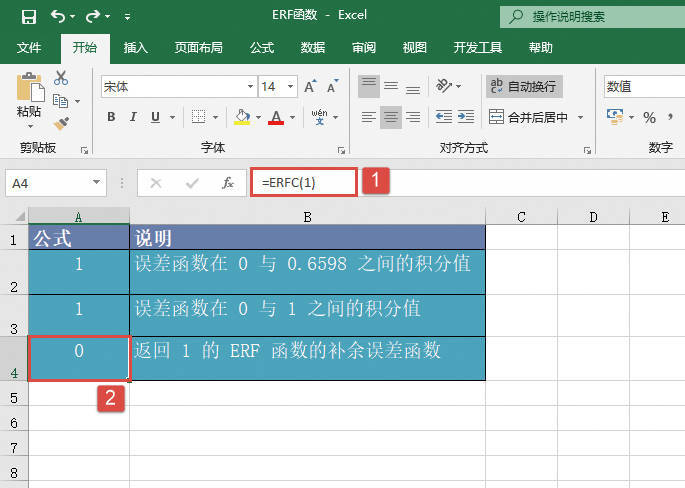
STEP03:选中A4单元格,在编辑栏中输入公式“=GESTEP(-7,-8)”,然后按“Enter”键返回,此时工作表结果显示为“1”,即检查出-7满足大于等于-8的条件,如图20-91所示。
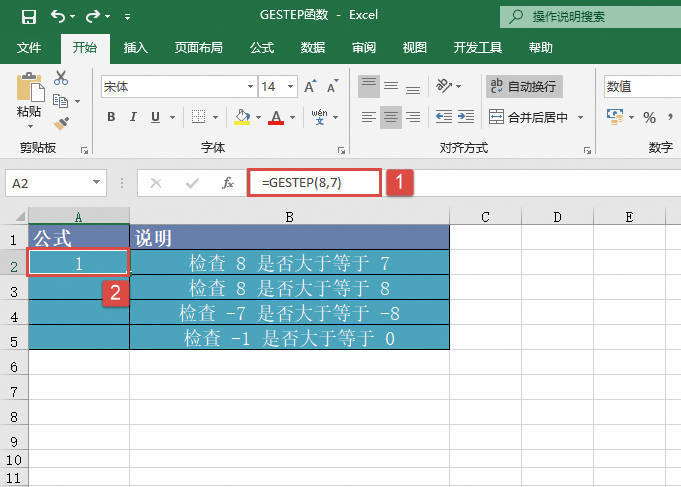
图20-89 检查8与7的关系
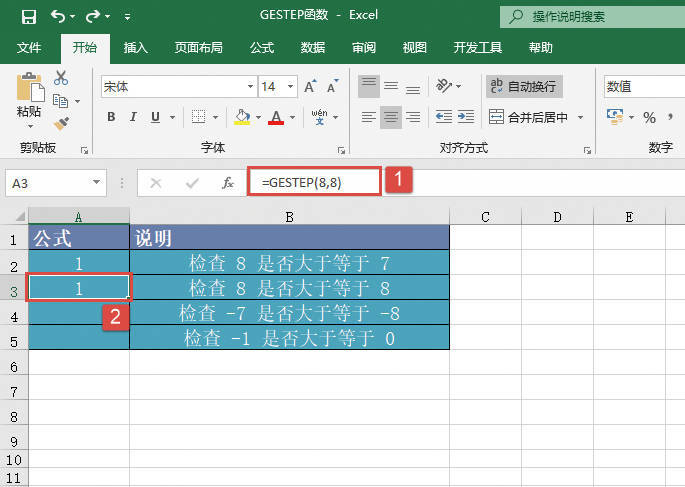
图20-90 检查8与8 的关系
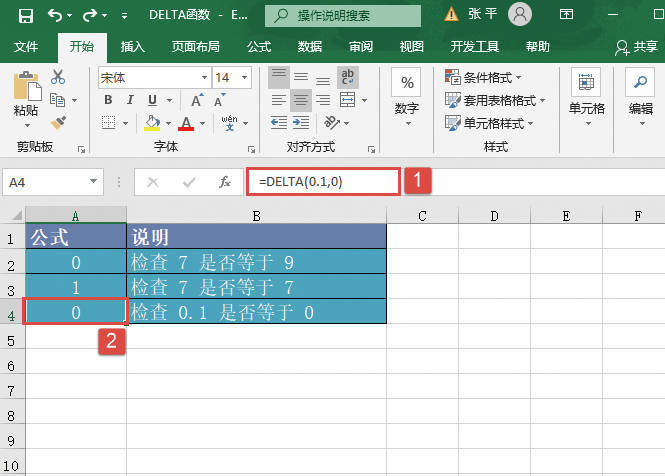
STEP04:选中A5单元格,在编辑栏中输入公式“=GESTEP(-1,0)”,然后按“Enter”键返回,此时工作表结果显示为“0”,即检查出-1不满足大于等于0的条件,如图20-92所示。
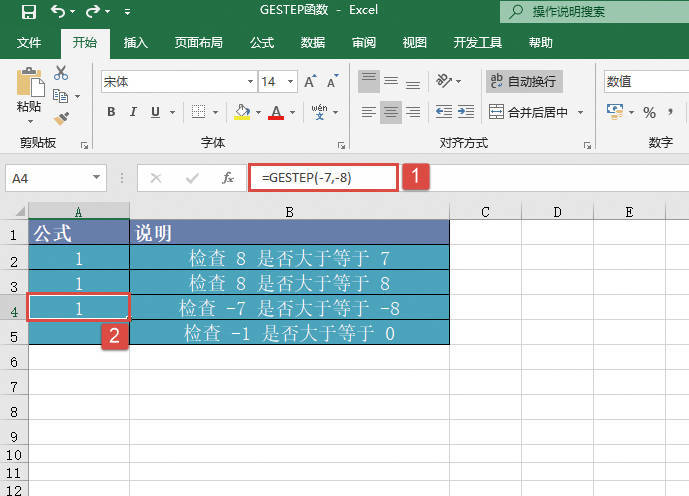
图20-91 检查-7与-8的关系
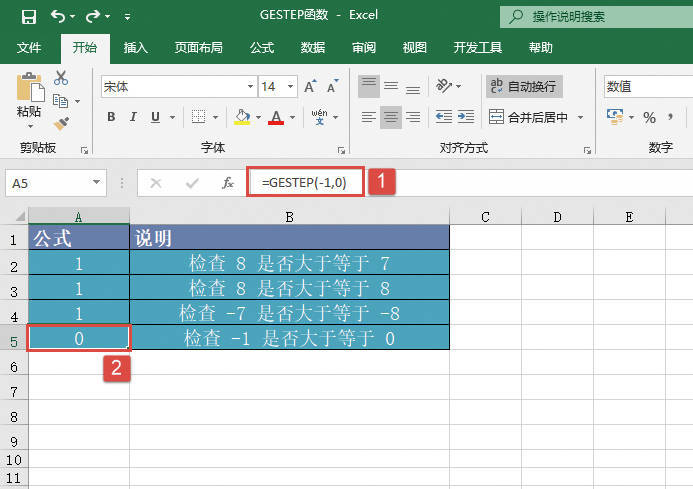
图20-92 检查-1与0的关系
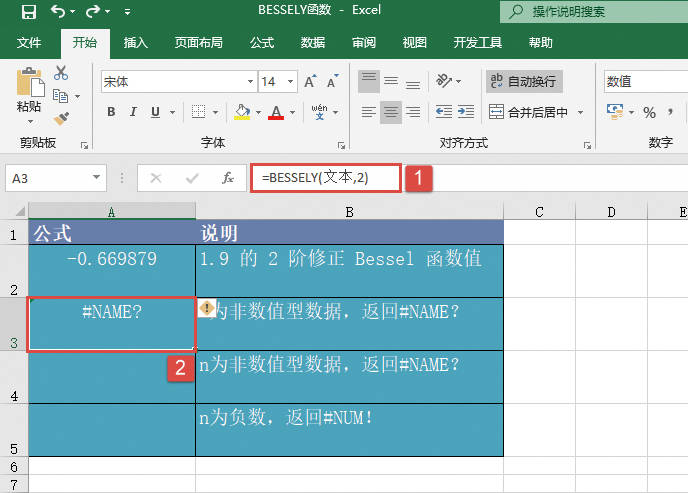
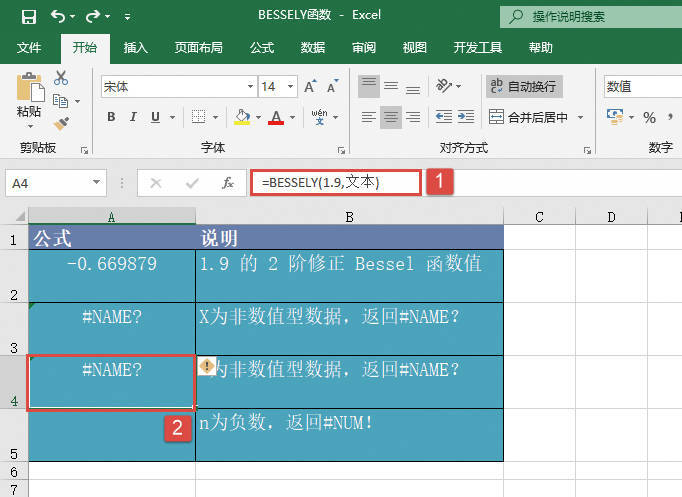
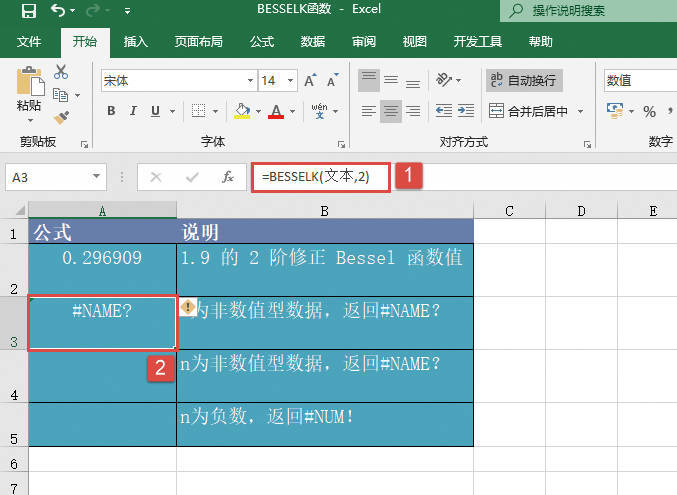
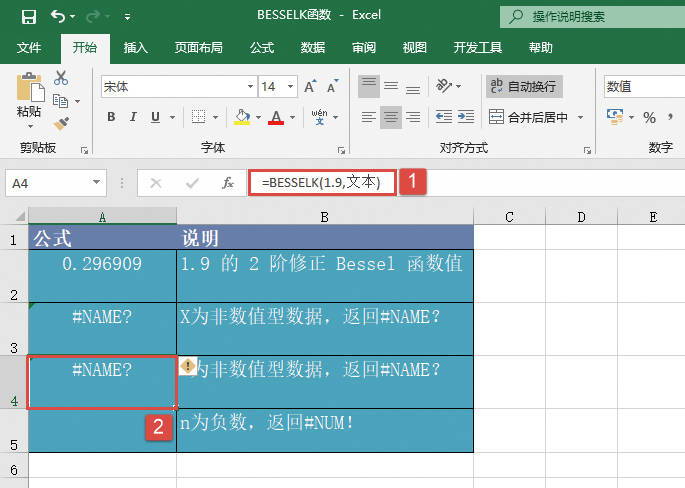
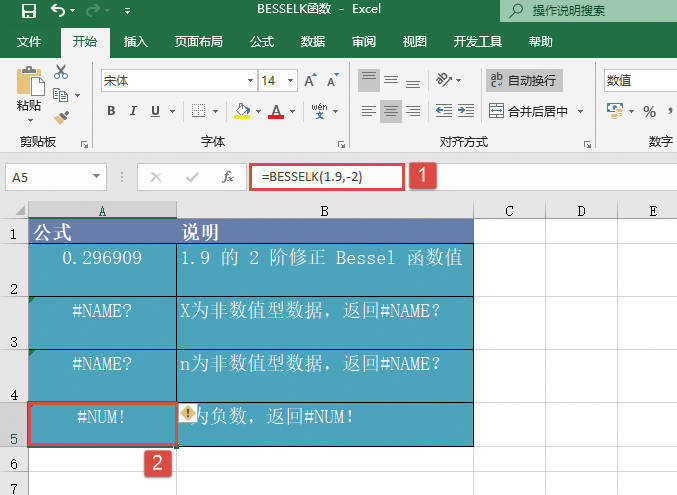
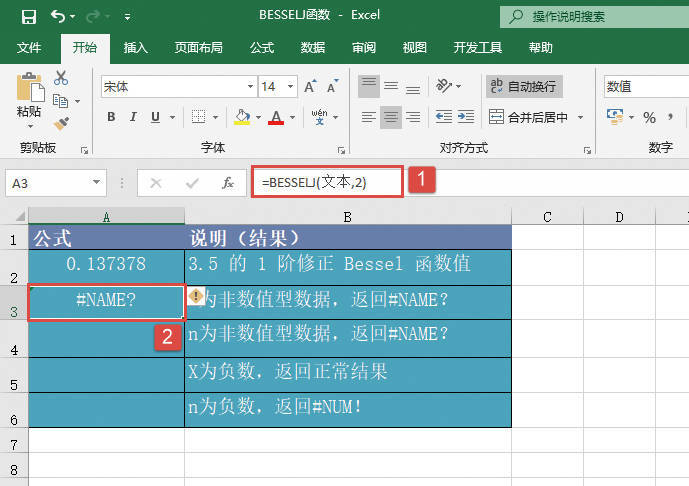
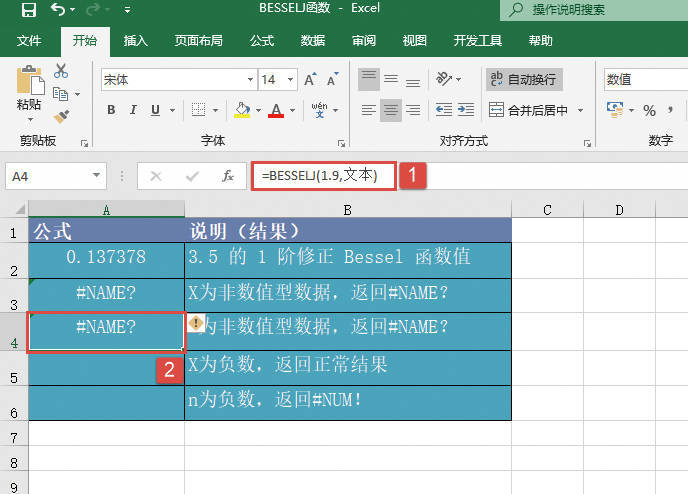
如果任一参数为非数值,则函数GESTEP返回错误值“#VALUE!”。
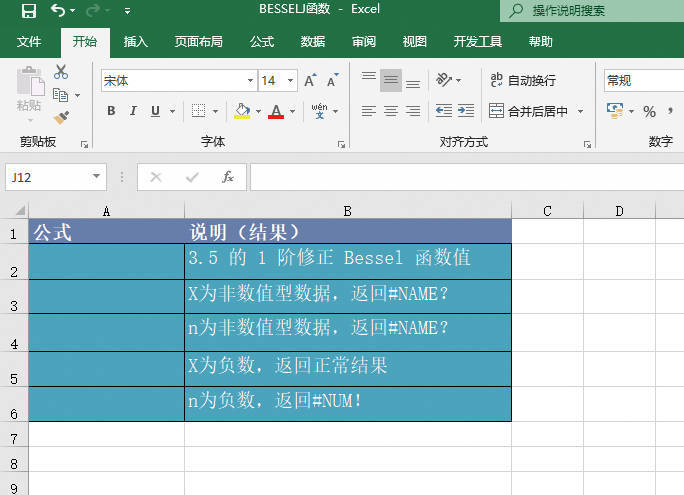
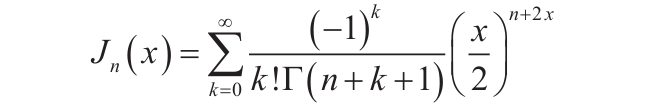
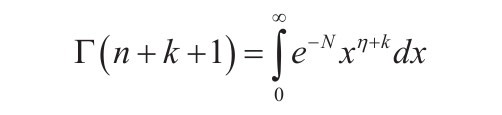
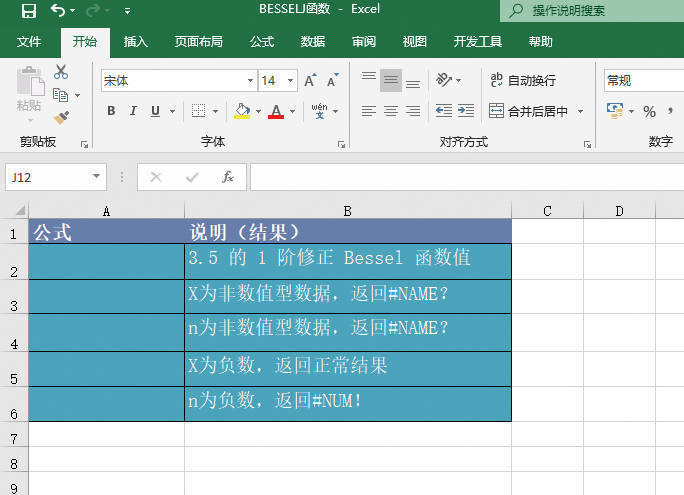
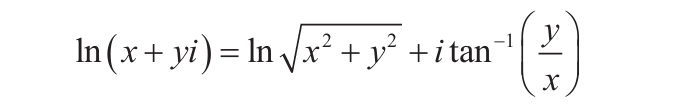
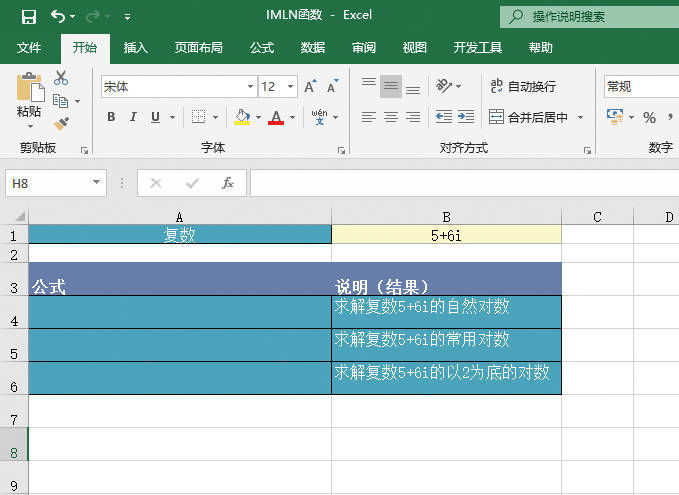
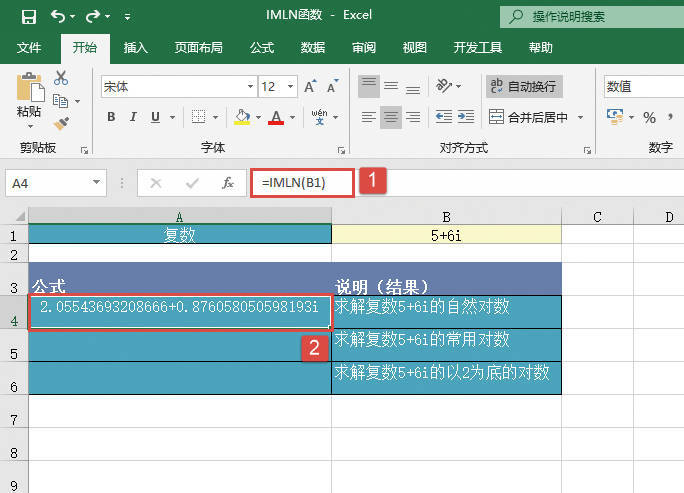
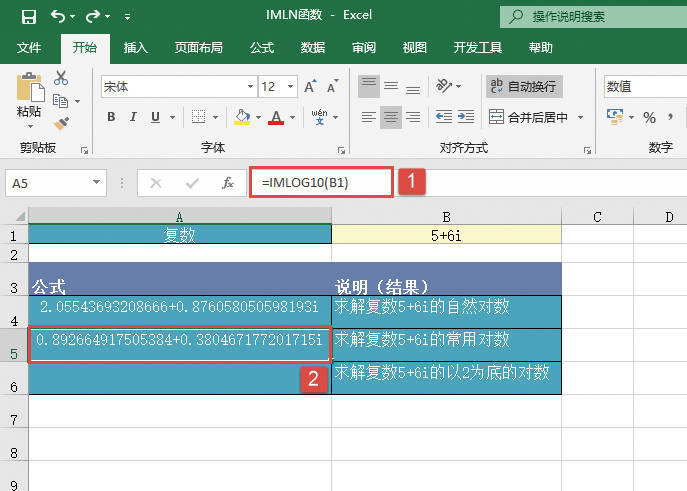
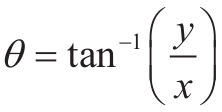 且θ∈[-π;π]
且θ∈[-π;π]