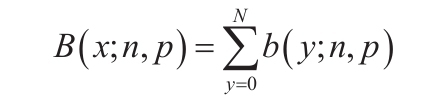分类：概率函数应用

概率分布是概率论的基本概念之一，用以表述随机变量取值的概率规律。为了使用的方便，可以根据随机变量所属类型的不同，利用Excel 2019提供的相关函数，获取概率分布不同的表现形式。

Excel 计算z检验的单尾概率值：ZTEST函数

ZTEST函数用于计算z检验的单尾概率值。对于给定的假设总体平均值μ0，ZTEST返回样本平均值大于数据集（数组）中观察平均值的概率，即观察样本平均值。ZTEST函数的语法如下：

ZTEST(array,μ0,sigma)

其中，array参数为用来检验μ0的数组或数据区域，μ0参数为被检验的值，sigma参数为样本总体（已知）的标准偏差，如果省略，则使用样本标准偏差。下面通过实例详细讲解该函数的使用方法与技巧。

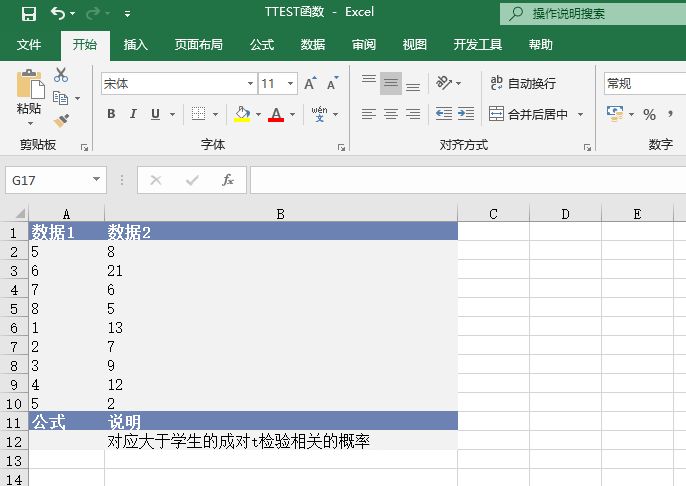
打开“ZTEST.xlsx”工作簿，切换至“Sheet1”工作表，本例中的原始数据如图17-25所示。工作表中记录了一组数据，要求根据工作表中的数据计算出z检验的概率值。具体的操作步骤如下。

图17-25　原始数据

STEP01：选中A13单元格，在编辑栏中输入公式“=ZTEST(A2:A11,4)”，用于计算总体平均值为4时数据集的z检验单尾概率值，输入完成后按“Enter”键返回计算结果，如图17-26所示。

STEP02：选中A14单元格，在编辑栏中输入公式“=2*MIN(ZTEST(A2:A11,4),1-ZTEST(A2:A11,4))”，用于计算总体平均值为4时数据集的z检验双尾概率值，输入完成后按“Enter”键返回计算结果，如图17-27所示。

STEP03：选中A15单元格，在编辑栏中输入公式“=ZTEST(A2:A11,6)”，用于计算总体平均值为6时数据集的z检验单尾概率值，输入完成后按“Enter”键返回计算结果，如图17-28所示。

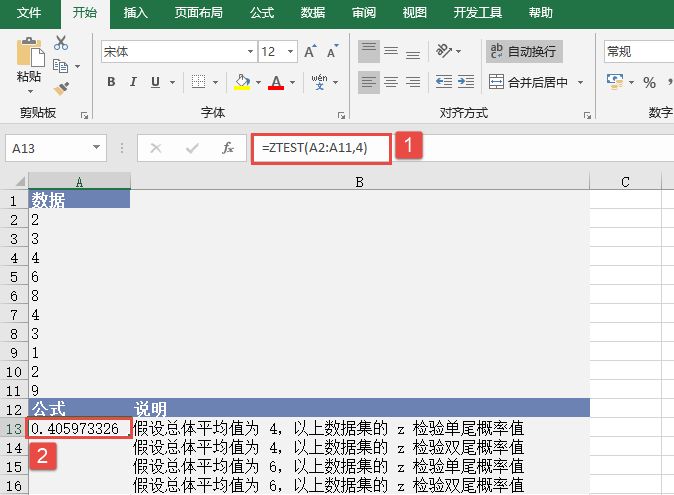
图17-26　计算z检验单尾概率值（一）

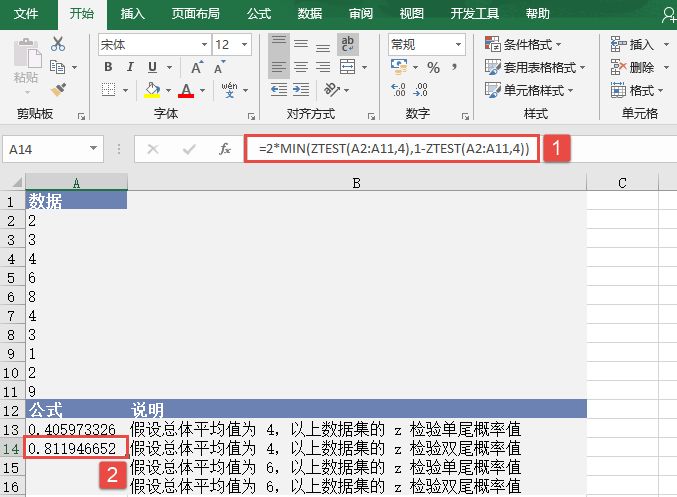
图17-27　计算z检验双尾概率值（一）

STEP04：选中A16单元格，在编辑栏中输入公式“=2*MIN(ZTEST(A2:A11,6),1-ZTEST(A2:A11,6))”，用于计算总体平均值为6时数据集的z检验双尾概率值，输入完成后按“Enter”键返回计算结果，如图17-29所示。

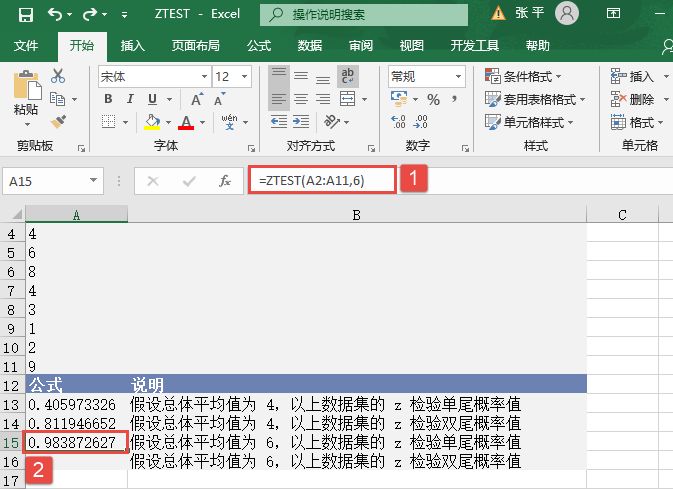
图17-28　计算z检验单尾概率值（二）

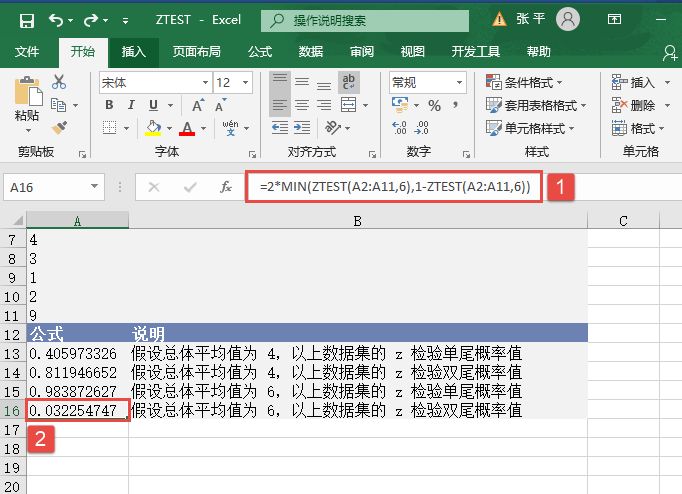
图17-29　计算z检验双尾概率值（二）

如果array为空，函数ZTEST返回错误值“#N/A”。不省略sigma时，函数ZTEST的计算公式如下：

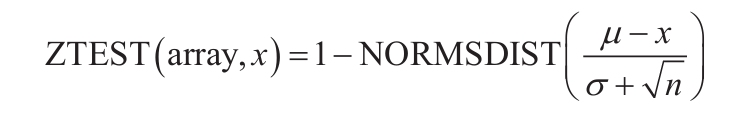
省略sigma时，函数ZTEST的计算公式如下：

其中，x为样本平均值AVERAGE(array)；s为样本标准偏差STDEV(array)；n为样本中的观察值个数COUNT(array)。

ZTEST表示当基础总体平均值为μ0时，样本平均值大于观察值AVERAGE(array)的概率。由于正态分布是对称的，如果AVERAGE(array)<μ0，则ZTEST的返回值将大于0.5。

当基础总体平均值为μ0，样本平均值从μ0（沿任一方向）变化到AVERAGE(array)时，下面的Excel公式可用于计算双尾概率：

=2*MIN(ZTEST(array,μ0,sigma),1-ZTEST(array,μ0,sigma))

Excel 计算t检验相关概率：TTEST函数

TTEST函数用于返回与学生t检验相关的概率。可以使用函数TTEST判断两个样本是否可能来自两个具有相同平均值的总体。TTEST函数的语法如下：

TTEST(array1,array2,tails,type)

其中，array1参数为第1个数据集，array2参数为第2个数据集，tails参数指示分布曲线的尾数，如果tails=1，函数TTEST使用单尾分布；如果tails=2，函数TTEST使用双尾分布。type参数为t检验的类型，如果type=1，则检验类型为成对；如果type=2，则检验类型为等方差双样本检验；如果type=3，则检验类型为异方差双样本检验。下面通过实例详细讲解该函数的使用方法与技巧。

打开“TTEST函数.xlsx”工作簿，切换至“Sheet1”工作表，本例中的原始数据如图17-23所示。工作表中记录了两个数据集，要求根据工作表中的数据计算与学生t检验相关的概率。具体的操作步骤如下。

选中A12单元格，在编辑栏中输入公式“=TTEST(A2:A10,B2:B10,2,1)”，用于计算对应于学生的成对t检验的概率，输入完成后按“Enter”键返回计算结果，如图17-24所示。

如果array1参数和array2参数的数据点个数不同，且type=1（成对），函数TTEST返回错误值“#N/A”。参数tails和type将被截尾取整。如果tails参数或type参数为非数值型，函数TTEST返回错误值“#VALUE!”。如果tails参数不为1或2，函数TTEST返回错误值“#NUM!”。TTEST使用array1和array2中的数据计算非负值t统计。如果tails=1，假设array1参数和array2参数为来自具有相同平均值的总体的样本，则TTEST返回t统计的较高值的概率；假设“总体平均值相同”，则当tails=2时返回的值是当tails=1时返回的值的两倍且符合t统计的较高绝对值的概率。

图17-23　原始数据

图17-24　计算t检验相关概率

Excel 计算F检验值：FTEST函数

FTEST函数用于计算F检验的结果。F检验返回的是当数组1和数组2的方差无明显差异时的单尾概率。可以使用FTEST函数来判断两个样本的方差是否不同。例如，给定几个不同学校的测试成绩，可以检验学校间测试成绩的差别程度。FTEST函数的语法如下：

FTEST(array1,array2)

其中，array1参数为第1个数组或数据区域，array2参数为第2个数组或数据区域。下面通过实例详细讲解该函数的使用方法与技巧。

已知在两个数据区域中，给定了两个不同学校不同科目在某一测试中成绩达到优秀分数线的学生数目，要求计算学校间测试成绩的差别程度。打开“FTEST函数.xlsx”工作簿，切换至“Sheet1”工作表，本例中的原始数据如图17-21所示。具体的操作步骤如下。

选中A8单元格，在编辑栏中输入公式“=FTEST(A2:A6,B2:B6)”，用于返回上述数据集的F检验结果，输入完成后按“Enter”键返回计算结果，如图17-22所示。

图17-21　原始数据

图17-22　计算F检验值

参数可以是数字，或者包含数字的名称、数组或引用。如果数组或引用参数包含文本、逻辑值或空白单元格，则这些值将被忽略；但包含零值的单元格将计算在内。如果数组1或数组2中数据点的个数小于2个，或者数组1或数组2的方差为零，函数FTEST返回错误值“#DIV/0!”。

Excel 计算独立性检验值：CHITEST函数

CHITEST函数用于计算独立性检验值。函数CHITEST返回χ2分布的统计值及相应的自由度。可以使用χ2检验值确定假设值是否被实验所证实。CHITEST函数的语法如下：

CHITEST(actual_range,expected_range)

其中，actual_range参数为包含观察值的数据区域，将对期望值做检验。expected_range参数为包含行列汇总的乘积与总计值之比率的数据区域。下面通过实例详细讲解该函数的使用方法与技巧。

打开“CHITEST函数.xlsx”工作簿，切换至“Sheet1”工作表，本例中的原始数据如图17-19所示。工作表中统计了某班男生与女生去某地旅游的意向，已知统计的实际数值与期望数值，要求计算出相关性检验值。具体的操作步骤如下。

选中A10单元格，在编辑栏中输入公式“=CHITEST(A2:B4,A6:B8)”，用于返回独立性检验值，输入完成后按“Enter”键返回计算结果，如图17-20所示。

图17-19　原始数据

图17-20　返回独立性检验值

如果actual_range参数和expected_range参数数据点的个数不同，则函数CHITEST返回错误值“#N/A”。χ2检验首先使用下面的公式计算χ2统计：

式中：

Aij=第i行、第j列的实际频率

Eij=第i行、第j列的期望频率

i=行数

j=列数

G=区间的上限

χ2的低值是独立的指示。从公式中可看出，χ2总是正数或0，且为0的条件是：对于每个i和j，如果Aij=Eij。

函数CHITEST返回在独立的假设条件下意外获得特定情况的概率，即χ2统计值至少和由上面的公式计算出的值一样大的情况。在计算此概率时，CHITEST使用具有相应自由度df的个数的χ2分布。如果r>1且c>1，则df=(r-1)(c-1)。如果r=1且c>1，则df=c–1。或者如果r>1且c=1，则df=r–1。若出现r=c=1，则返回“#N/A”。

当Eij的值不太小时，使用CHITEST最合适。某些统计人员建议每个Eij应该大于等于5。

Excel 计算泊松分布：POISSON函数

POISSON函数用于返回泊松分布。泊松分布通常用于预测一段时间内事件发生的次数，比如一分钟内通过收费站的轿车的数量。POISSON函数的语法如下：

POISSON(x,mean,cumulative)

其中，x参数为事件数，mean参数为期望值，cumulative参数为一逻辑值，确定所返回的概率分布形式。如果cumulative为TRUE，函数POISSON返回泊松累积分布概率，即，随机事件发生的次数在0到x之间（包含0和1）；如果为FALSE，则返回泊松概率密度函数，即随机事件发生的次数恰好为x。下面通过实例详细讲解该函数的使用方法与技巧。

打开“POISSON函数.xlsx”工作簿，切换至“Sheet1”工作表，本例中的原始数据如图17-16所示。已知事件数和期望值，要求计算符合这些条件的泊松累积分布概率和泊松概率密度函数的结果。具体的操作步骤如下。

图17-16　原始数据

STEP01：选中A5单元格，在编辑栏中输入公式“=POISSON(A2,A3,TRUE)”，用于计算符合上述条件的泊松累积分布概率，输入完成后按“Enter”键返回计算结果，如图17-17所示。

STEP02：选中A6单元格，在编辑栏中输入公式“=POISSON(A2,A3,FALSE)”，用于计算符合上述条件的泊松概率密度函数的结果，输入完成后按“Enter”键返回计算结果，如图17-18所示。

图17-17　计算符合上述条件的泊松累积分布概率

图17-18　计算泊松概率密度函数的结果

如果x参数不为整数，将被截尾取整。如果x参数或mean参数为非数值型，函数POISSON返回错误值“#VALUE!”。如果参数x<0，函数POISSON返回错误值“#NUM!”。如果参数mean<0，函数POISSON返回错误值“#NUM!”。函数POISSON的计算公式如下：

假设cumulative=FALSE，

假设cumulative=TRUE，

Excel 计算数值在指定区间内的概率：PROB函数

PROB函数用于返回区域中的数值落在指定区间内的概率。如果没有给出上限（upper_limit），则返回区间x_range内的值等于下限lower_limit的概率。PROB函数的语法如下：

PROB(x_range,prob_range,lower_limit,upper_limit)

其中，x_range参数为具有各自相应概率值的x数值区域，prob_range参数为与x_range中的值相对应的一组概率值，lower_limit参数为用于计算概率的数值下界，upper_limit参数为用于计算概率的可选数值上界。下面通过实例详细讲解该函数的使用方法与技巧。

打开“PROB函数.xlsx”工作簿，切换至“Sheet1”工作表，本例中的原始数据如图17-13所示。已知具备各自相应概率值的x数值区域，要求计算区域中的数值落在指定区间中的概率。具体的操作步骤如下。

图17-13　原始数据

STEP01：选中A7单元格，在编辑栏中输入公式“=PROB(A2:A5,B2:B5,2)”，用于计算x为2的概率，输入完成后按“Enter”键返回计算结果，如图17-14所示。

STEP02：选中A8单元格，在编辑栏中输入公式“=PROB(A2:A5,B2:B5,1,3)”，用于计算x在1到3之间的概率，输入完成后按“Enter”键返回计算结果，如图17-15所示。

图17-14　计算x为2的概率

图17-15　计算x在1到3之间的概率

如果prob_range参数中的任意值≤0或>1，函数PROB返回错误值“#NUM!”。如果prob_range参数中所有值之和不等于1，函数PROB返回错误值“#NUM!”。如果省略upper_limit参数，函数PROB返回值等于lower_limit时的概率。如果x_range参数和prob_range参数中的数据点个数不同，函数PROB返回错误值“#N/A”。

Excel 计算超几何分布：HYPGEOMDIST函数

HYPGEOMDIST函数用于计算超几何分布。给定样本容量、样本总体容量和样本总体中成功的次数，函数HYPGEOMDIST返回样本取得给定成功次数的概率。

使用函数HYPGEOMDIST可以解决有限总体的问题，其中每个观察值或者为成功或者为失败，且给定样本容量的每一个子集有相等的发生概率。HYPGEOMDIST函数的语法如下：

HYPGEOMDIST(sample_s,number_sample,population_s,number_population)

其中，sample_s参数为样本中成功的次数，number_sample参数为样本容量，population_s参数为样本总体中成功的次数，number_population参数为样本总体的容量。

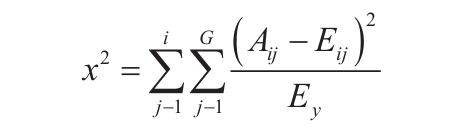
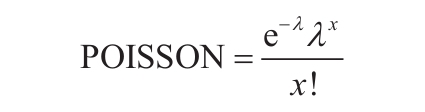
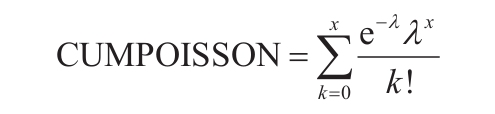
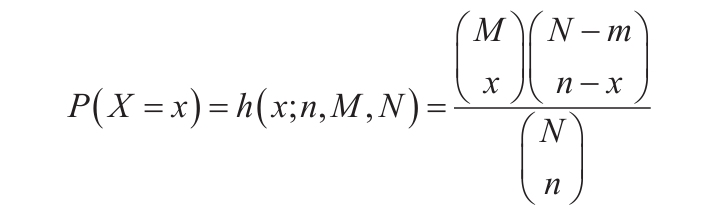
超几何分布的计算公式如下：

超几何分布的计算公式

式中：

x=sample_s

n=number_sample

M,m=population_s

N=number_population

下面通过实例详细讲解该函数的使用方法与技巧。

打开“HYPGEOMDIST函数.xlsx”工作簿，切换至“Sheet1”工作表，本例中的原始数据如图17-11所示。已知样本中成功的次数、样本容量、样本总体中成功的次数、样本总体的容量，要求计算样本和样本总体的超几何分布。具体的操作步骤如下。

选中A7单元格，在编辑栏中输入公式“=HYPGEOMDIST(A2,A3,A4,A5)”，用于返回上述样本和样本总体的超几何分布，输入完成后按“Enter”键返回计算结果，如图17-12所示。

如果任一参数为非数值型，函数HYPGEOMDIST返回错误值“#VALUE!”。如果参数sample_s<0或参数sample_s大于number_sample参数和population_s参数中的较小值，函数HYPGEOMDIST返回错误值“#NUM!”。如果sample_s参数小于0或(number_sample-number_population+population_s)中的较大值，函数HYPGEOMDIST返回错误值“#NUM!”。如果参数number_sample≤0或参数number_sample>number_population，函数HYPGEOMDIST返回错误值“#NUM!”。如果参数population_s≤0或参数population_s>number_population，函数HYPGEOMDIST返回错误值“#NUM!”。如果参数number_population≤0，函数HYPGEOMDIST返回错误值“#NUM!”。

图17-11　原始数据

返回上述样本和样本总体的超几何分布

图17-12　返回上述样本和样本总体的超几何分布

函数HYPGEOMDIST用于在有限样本总体中进行不退回抽样的概率计算。

Excel 计算F概率分布：FDIST函数

FDIST函数用于返回F概率分布。使用此函数可以确定两个数据集是否存在变化程度上的不同。例如，分析进入高中的男生、女生的考试分数，确定女生分数的变化程度是否与男生不同。FDIST函数的语法如下：

FDIST(x,degrees_freedom1,degrees_freedom2)

其中，x参数为参数值，degrees_freedom1参数为分子的自由度，degrees_freedom2参数为分母的自由度。下面通过实例详细讲解该函数的使用方法与技巧。

打开“FDIST函数.xlsx”工作簿，切换至“Sheet1”工作表，本例中的原始数据如图17-9所示。要求根据工作表中已经给定的参数值、分子自由度、分母自由度，计算F概率分布。具体的操作步骤如下。

选中A6单元格，在编辑栏中输入公式“=FDIST(A2,A3,A4)”，用于计算F概率分布，输入完成后按“Enter”键返回计算结果，如图17-10所示。

如果任何参数都为非数值型，函数FDIST返回错误值“#VALUE!”。如果x参数为负数，函数FDIST返回错误值“#NUM!”。如果degrees_freedom1参数或degrees_freedom2参数不是整数，将被截尾取整。如果参数degrees_freedom1<1或参数degrees_freedom1≥10^10，函数FDIST返回错误值“#NUM!”。如果参数degrees_freedom2<1或参数degrees_freedom2≥10^10，函数FDIST返回错误值“#NUM!”。函数FDIST的计算公式为FDIST=P(F>x)，其中F为呈F分布且带有degrees_freedom1和degrees_freedom2自由度的随机变量。

图17-9　原始数据

图17-10　计算F概率分布

Excel 计算χ2分布单尾概率：CHIDIST函数

CHIDIST函数用于返回χ2分布的单尾概率。χ2分布与χ2检验相关，使用χ2检验可以比较观察值和期望值。例如，某项遗传学实验假设下一代植物将呈现出某一组颜色。使用此函数比较观测结果和期望值，可以确定初始假设是否有效。CHIDIST函数的语法如下。

CHIDIST(x,degrees_freedom)

其中，x参数为用来计算分布的数值，degrees_freedom参数为自由度的数值。下面通过实例详细讲解该函数的使用方法与技巧。

打开“CHIDIST函数.xlsx”工作簿，切换至“Sheet1”工作表，本例中的原始数据如图17-5所示。工作表中已经给定用来计算分布的数值和自由度，要求计算χ2分布的单尾概率。具体的操作步骤如下。

选中A5单元格，在编辑栏中输入公式“=CHIDIST(A2,A3)”，用于计算χ2分布的单尾概率，输入完成后按“Enter”键返回计算结果，如图17-6所示。

图17-5　原始数据

图17-6　计算χ2分布的单尾概率

如果任一参数为非数值型，函数CHIDIST返回错误值“#VALUE!”。如果x为负数，函数CHIDIST返回错误值“#NUM!”。如果degrees_freedom参数不是整数，将被截尾取整。如果参数degrees_freedom<1或参数degrees_freedom>10^10，则函数CHIDIST返回错误值“#NUM!”。函数CHIDIST按CHIDIST=P(X>x)计算，式中X为χ2随机变量。

CHIINV函数用于返回χ2分布单尾概率的反函数值。如果probability=CHIDIST(x,…)，则CHIINV(probability,…)=x。使用此函数可比较观测结果和期望值，以确定初始假设是否有效。CHIINV函数的语法如下：

CHIINV(probability,degrees_freedom)

其中，probability参数为与χ2分布相关的概率，degrees_freedom参数为自由度的数值。下面通过实例详细讲解该函数的使用方法与技巧。

打开“CHIINV函数.xlsx”工作簿，切换至“Sheet1”工作表，本例中的原始数据如图17-7所示。工作表中已经给定用来计算分布的数值和自由度，要求计算χ2分布的单尾概率的反函数值。具体的操作步骤如下。

选中A5单元格，在编辑栏中输入公式“=CHIINV(A2,A3)”，用于计算χ2分布的单尾概率的反函数值，输入完成后按“Enter”键返回计算结果，如图17-8所示。

图17-7　原始数据

计算χ2分布的单尾概率的反函数值

图17-8　计算χ2分布的单尾概率的反函数值

如果任一参数为非数字型，则函数CHIINV返回错误值“#VALUE!”。如果probability<0或probability>1，则函数CHIINV返回错误值“#NUM!”。如果degrees_freedom不是整数，将被截尾取整。如果degrees_freedom<1或degrees_freedom≥10^10，函数CHIINV返回错误值“#NUM!”。如果已给定概率值，则CHIINV使用CHIDIST(x,degrees_freedom)=probability求解数值x。因此，CHIINV的精度取决于CHIDIST的精度。CHIINV使用迭代搜索技术。如果搜索在100次迭代之后没有收敛，则函数返回错误值“#N/A”。

Excel 计算一元二项式分布概率值：BINOMDIST函数

BINOMDIST函数可以返回一元二项式分布的概率值。函数BINOMDIST适用于固定次数的独立试验，试验的结果只包含成功或失败两种情况，且成功的概率在实验期间固定不变。例如，函数BINOMDIST可以计算3个婴儿中两个是男孩的概率。BINOMDIST函数的语法如下：

BINOMDIST(number_s,trials,probability_s,cumulative)

其中，number_s参数为试验成功的次数。trials参数为独立试验的次数。probability_s参数为每次试验中成功的概率。cumulative参数为一逻辑值，决定函数的形式。如果cumulative参数为TRUE，函数BINOMDIST返回累积分布函数，即至多number_s次成功的概率；如果为FALSE，返回概率密度函数，即number_s次成功的概率。下面通过实例详细讲解该函数的使用方法与技巧。

已知工厂中某次产品试验的成功次数为8，独立试验次数为12，每次试验的成功概率为0.6，要求计算12次试验中成功6次的概率。打开“BINOMDIST函数.xlsx”工作簿，切换至“Sheet1”工作表，本例中的原始数据如图17-3所示。具体的操作步骤如下。

选中A6单元格，在编辑栏中输入公式“=BINOMDIST(A2,A3,A4,FALSE)”，用于计算12次试验成功6次的概率，输入完成后按“Enter”键返回计算结果，如图17-4所示。

图17-3　原始数据

图17-4　计算12次试验成功6次的概率

如果参数number_s、trials或probability_s为非数值型，函数BINOMDIST返回错误值“#VALUE!”。如果参数number_s<0或参数number_s>trials，函数BINOMDIST返回错误值“#NUM!”。如果参数probability_s<0或参数probability_s>1，函数BINOMDIST返回错误值“#NUM!”。一元二项式概率密度函数的计算公式为：

式中：

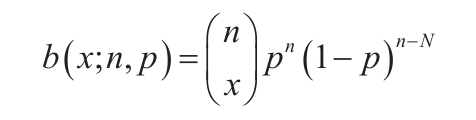
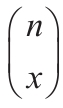等于COMBIN(n,x)。

一元二项式累积分布函数的计算公式为：