分类：Excel2019函数公式大全

“回归”分析工具通过对一组观察值使用“最小二乘法”直线拟合来执行线性回归分析。本工具可用来分析单个因变量是如何受一个或几个自变量的值影响的。例如，观察某个运动员的运动成绩与一系列统计因素（如年龄、身高和体重等）的关系。可以基于一组已知的成绩统计数据，确定这3个因素分别在运动成绩测试中所占的比重，然后使用该结果对尚未进行过测试的运动员的表现进行预测。“回归”工具使用工作表函数LINEST。

下面通过实例说明如何进行回归分析。

STEP01：打开“回归分析.xlsx”工作簿，将要处理的数据输入工作表中，本例中的原始数据如图22-54所示。

STEP02：选中工作表中的任意一个单元格，如B1单元格，切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图22-55所示的“数据分析”对话框。在“分析工具”列表框中选择“回归”选项，然后单击“确定”按钮。

图22-54　原始数据

图22-55　选择“回归”分析工具

STEP03：随后会打开“回归”对话框，在“输入”列表区域中设置Y值输入区域为“$A$4:$A$13”，设置X值输入区域为“$B$4:$B$13”，勾选“标志”复选框与“置信度”复选框，并设置置信度为“95%”。然后在“输出选项”列表区域中单击选中“新工作表组”单选按钮，在“残差”列表区域中依次勾选“残差”、“残差图”、“标准残差”及“线性拟合图”复选框，最后在“正态分布”列表区域中勾选“正态概率图”复选框。设置完成后单击“确定”按钮即可返回工作表，如图22-56所示。

图22-56　设置回归参数

根据需要设置以下选项。

1）Y值输入区域：输入对因变量数据区域的引用，该区域必须由单列数据组成。

2）X值输入区域：输入对自变量数据区域的引用，Excel将对此区域中的自变量从左到右进行升序排列。自变量的个数最多为16。

3）置信度：如果需要在汇总输出表中包含附加的置信度信息，则选中此复选框。在右侧的框中输入所要使用的置信度，默认值为95%。

4）常数为零：如果要强制回归线经过原点，则选中此复选框。

5）输出区域：输入对输出表左上角单元格的引用。汇总输出表至少需要有6列，其中包括方差分析表、系数、y估计值的标准误差、r2值、观察值个数以及系数的标准误差。

6）残差：如果需要在残差输出表中包含残差，则选中此复选框。

7）标准残差：如果需要在残差输出表中包含标准残差，则选中此复选框。

8）残差图：如果需要为每个自变量及其残差生成一张图表，则选中此复选框。

9）线性拟合图：如果需要为预测值和观察值生成一张图表，则选中此复选框。

10）正态概率图：如果需要生成一张图表来绘制正态概率，则选中此复选框。

STEP04：此时，“Sheet1”工作表前会自动新建一张新的工作表“Sheet4”，工作表中会显示回归分析的具体结果，如图22-57所示。

图22-57　回归分析结果

“随机数发生器”分析工具可用几个分布之一产生的独立随机数来填充某个区域。可以通过概率分布来表示总体中的主体特征。例如，可以使用正态分布来表示人体身高的总体特征，或者使用双值输出的伯努利分布来表示掷币实验结果的总体特征。

下面通过实例说明如何进行随机数发生器分析。

STEP01：打开“随机数发生器.xlsx”工作簿，切换至“Sheet1”工作表，在A1单元格、B1单元格和C1单元格中分别输入文本“变量1”“变量2”和“变量3”，如图22-50所示。

STEP02：选中工作表中的任意一个单元格，如B1单元格，切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图22-51所示的“数据分析”对话框。在“分析工具”列表框中选择“随机数发生器”选项，然后单击“确定”按钮。

STEP03：随后会打开“随机数发生器”对话框，在“变量个数”文本框中输入“3”，在“随机数个数”文本框中输入“12”，单击“分布”选择框右侧的下拉按钮，在展开的下拉列表中选择“正态”选项，在“参数”列表区域中设置平均值为“10”，标准偏差为“3”。然后在“输出选项”列表区域中单击选中“输出区域”单选按钮，并设置输出区域为“$A$2”单元格，最后单击“确定”按钮返回工作表，如图22-52所示。

图22-50　输入文本

图22-51　选择分析工具

其中一些不同于其他分析工具的选项简要介绍如下。

1）随机数个数：在此输入要查看的数据点个数。每一个数据点出现在输出表的一行中。如果没有输入数字，Excel会在指定的输出区域中填充所有的行。

2）分布：在此选择用于创建随机数的分布方法。Excel 2019共提供了7种随机数的分布方法：均匀、正态、伯努利、二项式、泊松、模式和离散。

图22-52　设置随机数发生器参数

·均匀：以下限和上限来表征。其变量是通过对区域中的所有数值进行等概率抽取而得到的。普通的应用是在范围0到1之间的均匀分布。

·正态：以平均值和标准偏差来表征。普通的应用是平均值为0、标准偏差为1的标准正态分布。

·伯努利：以给定的试验中成功的概率（p值）来表征。伯努利随机变量的值为0或1。例如，可以在范围0到1之间抽取均匀分布随机变量。如果变量小于或等于成功的概率，则伯努利随机变量的值为1，否则，随机变量的值为0。

·二项式：以一系列试验中成功的概率（p值）来表征。例如，可以按照“试验次数”框中指定的个数生成一系列伯努利随机变量，这些变量之和为一个二项式随机变量。

·泊松：以值λ来表征，λ等于平均值的倒数。泊松分布经常用于表示单位时间内事件发生的次数，例如，汽车到达收费停车场的平均速率。

·模式：以上界和下界、步长、数值重复率以及序列重复率来表征。

·离散：以数值及相应的概率区域来表征。在本对话框中给定的输入区域必须包含两列，左边一列包含数值，右边一列为与数值对应的发生概率。所有概率的和必须为1。

3）参数：在此输入用于表征选定分布的数值。

4）随机数基数：在此输入用来构造随机数的可选数值。可以在以后重新使用该数值来生成相同的随机数。

STEP04：此时，工作表中会显示“随机数发生器”的分析结果，如图22-53所示。

图22-53　随机数发生器分析结果

“直方图”分析工具可计算数据单元格区域和数据接收区间的单个和累积频率。此工具可用于统计数据集中某个数值出现的次数。

例如，在一个有20名学生的班里，可按字母评分的分类来确定成绩的分布情况。直方图表可给出字母评分的边界，以及在最低边界和当前边界之间分数出现的次数。出现频率最多的分数即为数据集中的众数。下面通过实例说明如何进行直方图分析。

STEP01：打开“直方图分析.xlsx”工作簿，将要处理的数据输入工作表中，本例中的原始数据如图22-46所示。

图22-46　原始数据

STEP02：选中工作表中的任意一个单元格，如B3单元格，切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图22-47所示的“数据分析”对话框。在“分析工具”列表框中选择“直方图”选项，然后单击“确定”按钮。

图22-47　选中“直方图“分析工具

STEP03：随后会打开“直方图”对话框，在“输入”列表区域设置输入区域为“$C$4:$C$23”，接收区域为“$E$4:$E$14”，然后在“输出选项”列表区域中单击选中“输出区域”单选按钮，并设置输出区域为“$G$3”单元格，依次勾选“柏拉图”“累积百分率”和“图表输出”复选框，最后单击“确定”按钮返回工作表，如图22-48所示。

其中一些不同于其他分析工具的选项简要介绍如下。

1）接收区域（可选）：在此输入接收区域的单元格引用，该区域包含一组可选的用来定义接收区域的边界值。这些值应当按升序排列。Excel将统计在当前边界值和相邻边界值之间的数据点个数（如果存在）。如果数值等于或小于边界值，则该值将被归到以该边界值为上限的区域中进行计数。所有小于第1个边界值的数值将一同计数；同样，所有大于最后一个边界值的数值也将一同计数。

2）柏拉图：选中此复选框可以在输出表中按降序来显示数据。如果此复选框被清除，Excel将只按升序来显示数据并省略最右边包含排序数据的3列数据。

3）累积百分率：选中此复选框可以在输出表中生成一列累积百分比值，并在直方图中包含一条累积百分比线。如果清除此选项，则会省略累积百分比。

4）图表输出：选中此复选框可以在输出表中生成一个嵌入直方图。

STEP04：此时，工作表中会显示“直方图”的分析结果，如图22-49所示。

图22-48　设置直方图分析参数

图22-49　直方图分析结果

“描述统计”分析工具用于生成数据源区域中数据的单变量统计分析报表，提供有关数据趋中性和易变性的信息。

下面通过实例说明如何进行描述统计分析。

STEP01：打开“描述统计分析.xlsx”工作簿，将要处理的数据输入工作表中，本例中的原始数据如图22-42所示。

STEP02：选中工作表中的任意一个单元格，如B1单元格，切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图22-43所示的“数据分析”对话框。在“分析工具”列表框中选择“描述统计”选项，然后单击“确定”按钮。

图22-42　原始数据

图22-43　选择“描述统计”分析工具

STEP03：随后会打开“描述统计”对话框，在“输入”列表区域设置输入区域为“$B$2:$B$25”，在“分组方式”列表下单击选中“逐列”单选按钮。然后在“输出选项”列表区域中单击选中“输出区域”单选按钮，并设置输出区域为“$D$2”单元格，勾选“汇总统计”复选框，最后单击“确定”按钮返回工作表，如图22-44所示。

其中一些不同于其他分析工具的选项简要介绍如下。

1）汇总统计：选中此项可以为结果输出表中每个统计结果生成一个字段，包括平均值、标准误差、中值、众数、标准偏差、方差、峰值、偏斜度、极差、最小值、最大值、总和、计数、最大值（#）、最小值（#）和置信度。

2）平均数置信度：如果需要在输出表的某一行中包含平均数置信度，则选中“平均数置信度”复选框，并在右侧的文本框中输入所要使用的置信度。例如，数值95%用来计算在显著性水平为5%时的平均值置信度。此处使用默认值95%。

3）第K大值：如果需要在输出表的某一行中包含每个数据区域中的第K个最大值，则选中“第K最大值”复选框。在右侧的文本框中，输入K的数字。如果输入1，则该行将包含数据集中的最大值。此处使用默认值1。

4）第K小值：如果需要在输出表的某一行中包含每个数据区域中的第K个最小值，则选中“第K最小值”复选框。在右侧的文本框中，输入K的数字。如果输入1，则该行将包含数据集中的最小值。此处使用默认值1。

STEP04：此时，工作表中会显示“描述统计”的分析结果，如图22-45所示。

图22-44　设置“描述统计”参数

图22-45　描述统计分析结果

相关系数与协方差一样是描述两个测量值变量之间的离散程度的指标。与协方差的不同之处在于，相关系数是成比例的，因此它的值与这两个测量值变量的表示单位无关。例如，如果两个测量值变量为重量和高度，当重量单位从磅换算成千克时，相关系数的值并不改变。任何相关系数的值都必须为-1～+1（包括-1和+1）。

可以使用相关系数分析工具来检验每对测量值变量，以便确定两个测量值变量是否趋向于同时变动，即，一个变量的较大值是否趋向于与另一个变量的较大值相关联（正相关）；或者一个变量的较小值是否趋向于与另一个变量的较大值相关联（负相关）；或者两个变量的值趋向于互不关联（相关系数近似于零）。

下面通过实例说明如何进行相关系数分析。

STEP01：打开“相关系数分析.xlsx”工作簿，将要处理的数据输入工作表中，本例中的原始数据如图22-38所示。

STEP02：选中工作表中的任意一个单元格，如B3单元格，切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图22-39所示的“数据分析”对话框。在“分析工具”列表框中选择“相关系数”选项，然后单击“确定”按钮。

图22-38　原始数据

图22-39　选择“相关系数”分析工具

STEP03：随后会打开“相关系数”对话框，在“输入”列表区域设置输入区域为“$B$4:$G$5”，在“分组方式”列表下单击选中“逐行”单选按钮。然后在“输出选项”列表区域中单击选中“输出区域”单选按钮，并设置输出区域为“$A$7”单元格，最后单击“确定”按钮返回工作表，如图22-40所示。

STEP04：此时，工作表中会显示“相关系数”的分析结果，如图22-41所示。

图22-40　设置相关系数参数

图22-41　相关系数分析结果

从相关系数分析结果可以看出，月销售额与销售成本之间的相关系数达到了0.990317，说明两者之间呈现良好的正相关性。

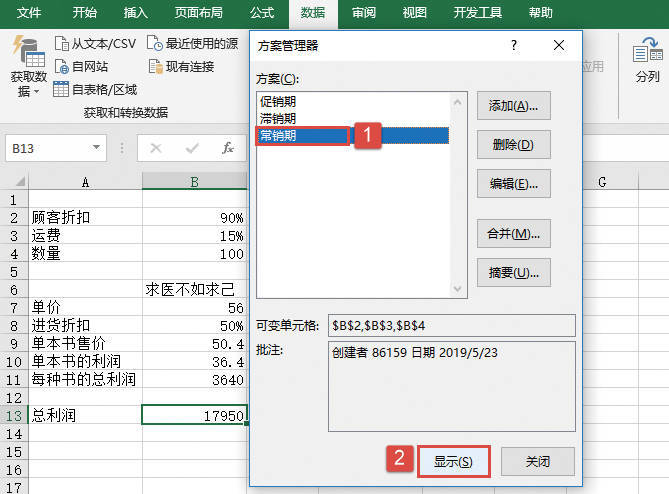
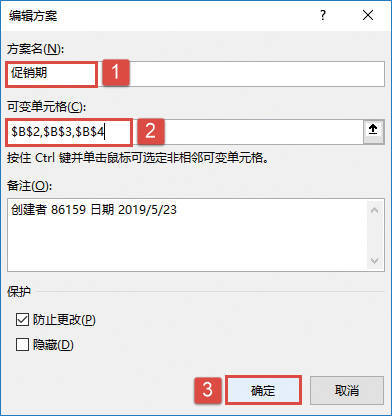
方差分析工具提供了以下3种不同类型的方差分析：单因素方差分析、包含重复的双因素方差分析和无重复的双因素方差分析。具体应该使用何种工具，需要根据因素的个数以及待检验样本总体中所含样本的个数而定。

单因素方差分析

也叫作一维方差分析，此工具可对两个或更多样本的数据执行简单的方差分析。此分析可提供一种假设测试，该假设的内容是：每个样本都取自相同的基础概率分布，而不是对所有样本来说基础概率分布都不相同。如果只有两个样本，则可使用工作表函数TTEST。如果有两个以上的样本，则没有使用方便的TTEST归纳，可改为调用“单因素方差分析”模型。

下面通过实例说明如何进行单因素方差分析。

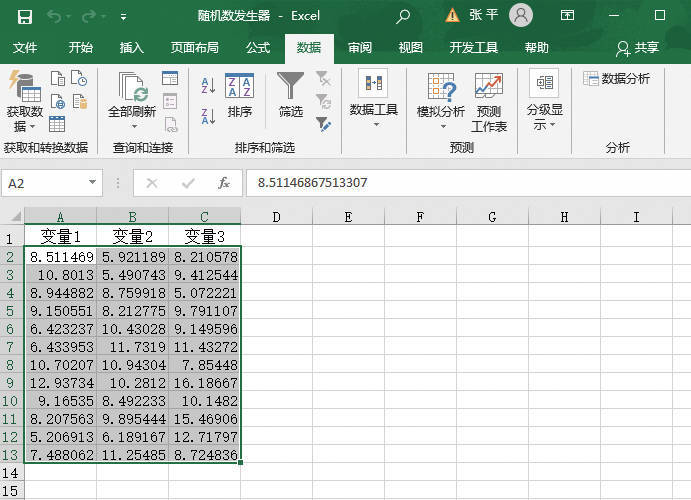
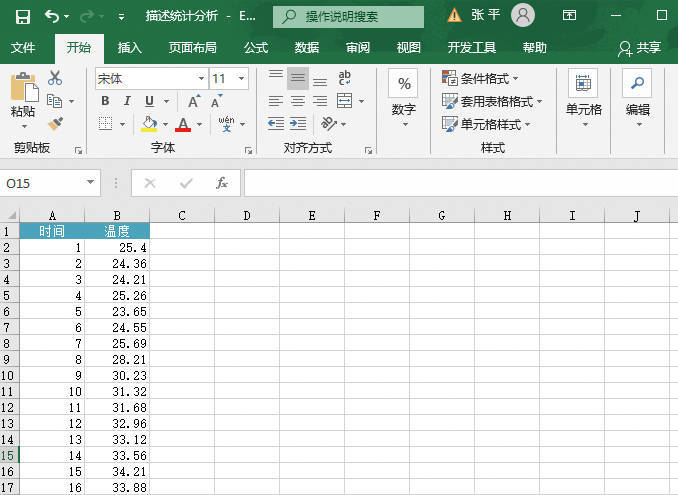
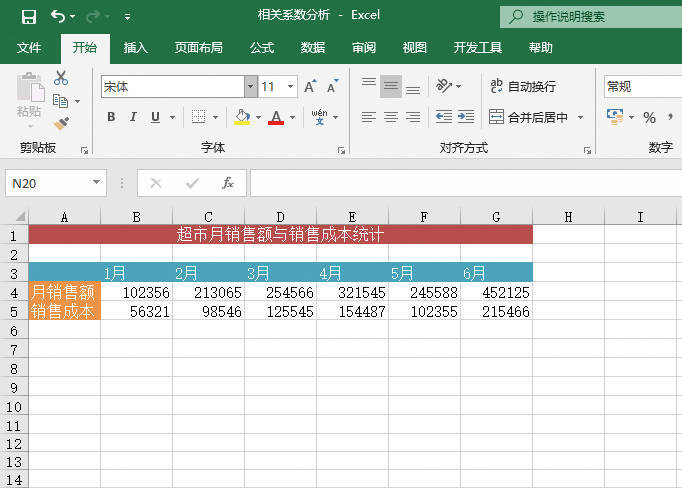
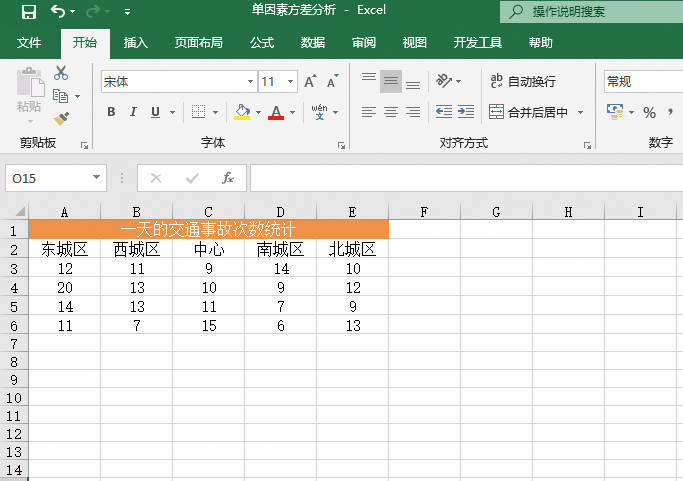
STEP01：打开“单因素方差分析.xlsx”工作簿，将要处理的数据输入工作表中。本例将5个地区一天当中发生交通事故的次数输入工作表，原始数据如图22-25所示。下面将以α=0.01检验各地区平均每天交通事故的次数是否相等。

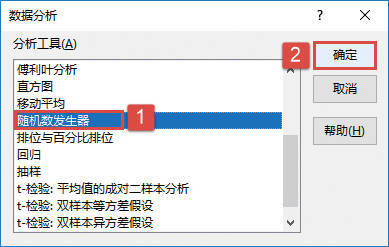
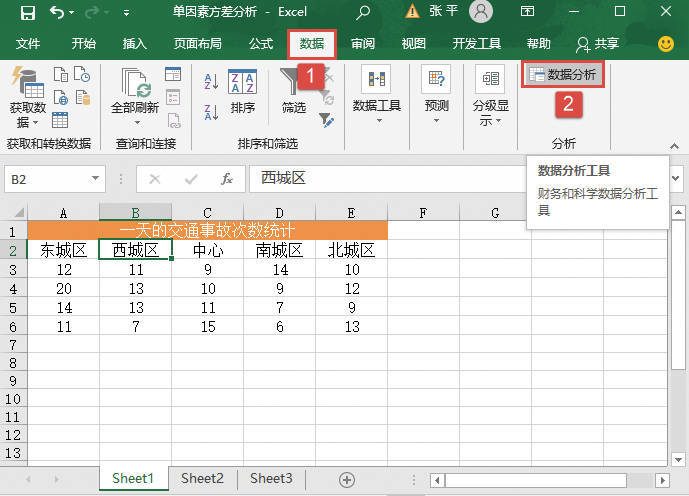
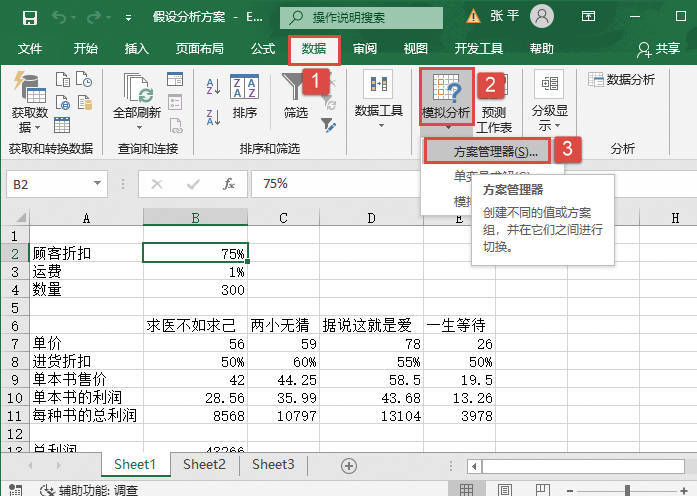
STEP02：选中工作表中的任意一个单元格，如B2单元格，切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮打开“数据分析”对话框，如图22-26所示。

图22-25　原始数据

图22-26　单击“数据分析”按钮

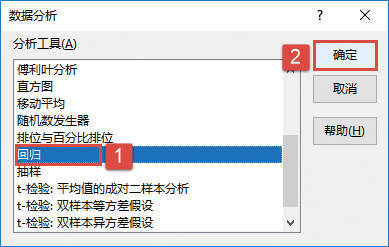
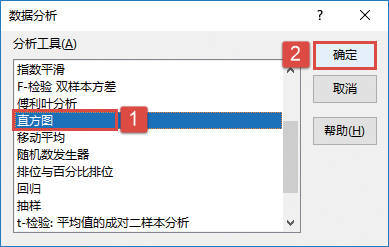
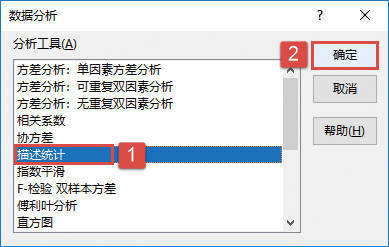
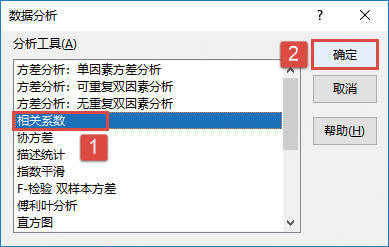
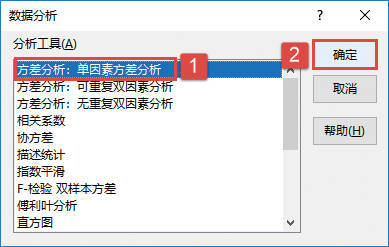
STEP03：打开“数据分析”对话框后，在“分析工具”列表框中选择“方差分析：单因素方差分析”选项，然后单击“确定”按钮，如图22-27所示。

图22-27　选择分析工具

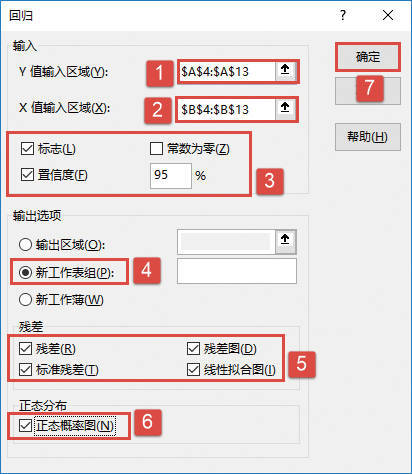
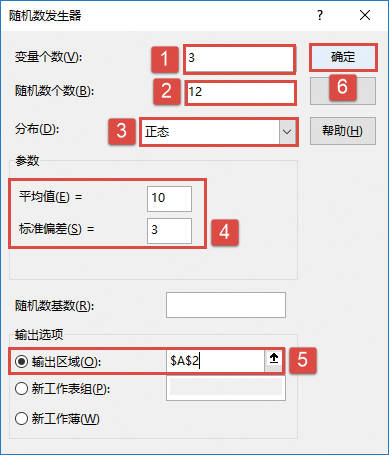
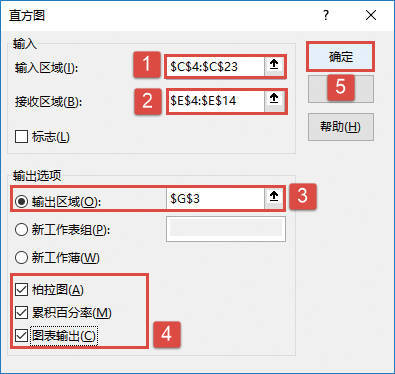
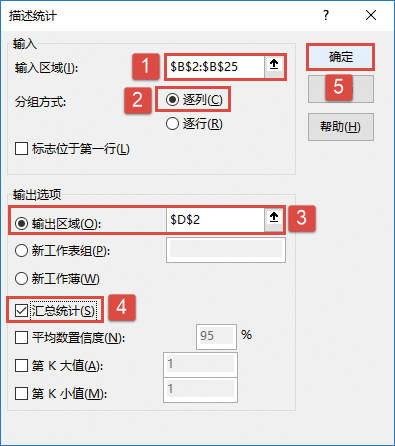
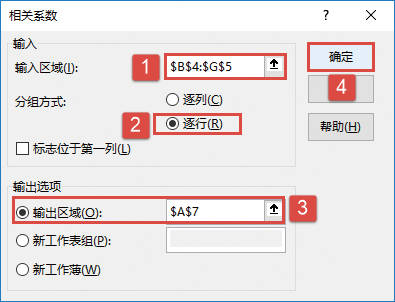
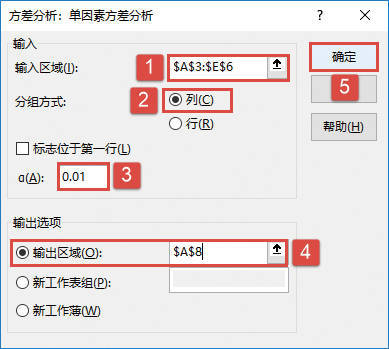
STEP04：随后会打开“方差分析：单因素方差分析”对话框，在“输入”列表区域设置输入区域为“$A$3:$E$6”，在“分组”方式列表中单击选中“列”单选按钮，设置α的值为“0.01”。然后在“输出选项”列表区域中单击选中“输出区域”单选按钮，并设置输出区域为“$A$8”单元格，最后单击“确定”按钮返回工作表，如图22-28所示。

对话框中各选项简要介绍如下。

1）输入区域：输入待分析数据区域的单元格引用，该引用必须由两个或两个以上按列或行排列的数据区域组成。

2）分组方式：如果要指定输入区域中的数据是按行还是按列排列，则选择“行”或“列”单选按钮。

3）标志位于第一行/标志位于第一列：如果输入区域的第1行中包含标志项，则选中“标志位于第一行”复选框。如果输入区域的第1列中包含标志项，则选中“标志位于第一列”复选框。如果输入区域没有标志项，则不选择该复选框，Excel将在输出表中生成合适的标志项。

4）α：输入要用来计算F统计的临界值的置信度。α置信度为与I型错误发生概率相关的显著性水平（拒绝真假设）。

5）输出区域：输入对输出表左上角单元格的引用，Excel只在输出表的半边填写结果，这是因为两个区域中数据的协方差与区域被处理的次序无关。在输出表的对角线上为每个区域的方差。

6）新工作表组：选择此项可以在当前工作簿中插入新工作表，并由新工作表的A1单元格开始粘贴计算结果。如果要为新工作表命名，则在右侧的文本框中输入名称。

7）新工作簿：选择此项可以创建一个新的工作簿，并在新工作簿的新工作表中粘贴计算结果。

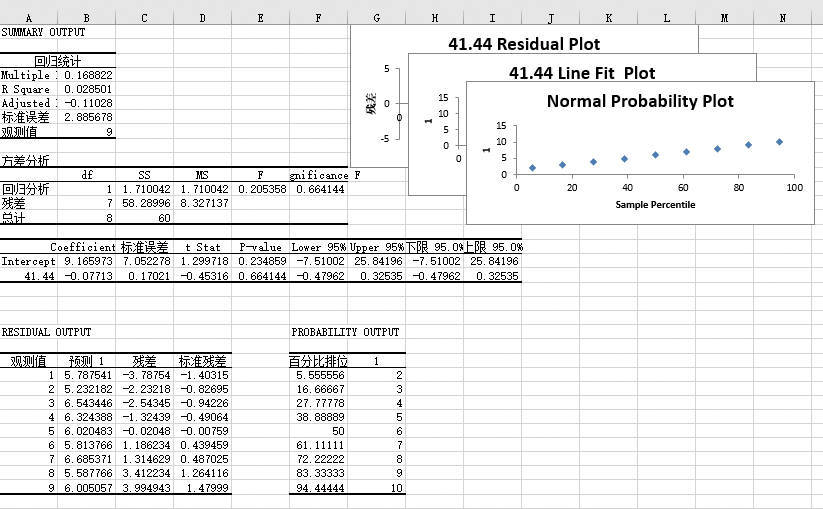
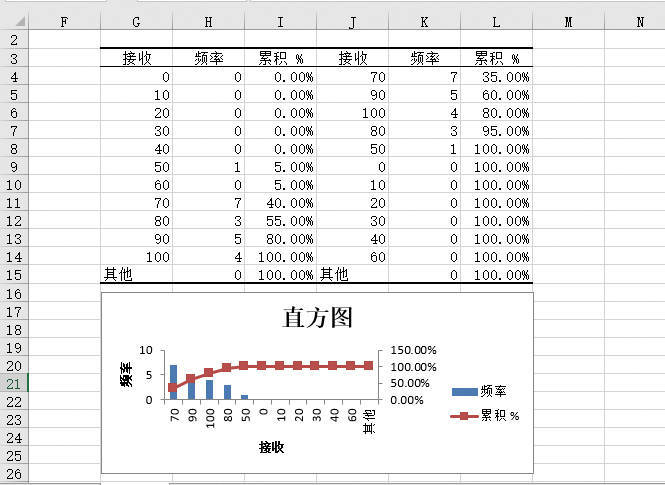
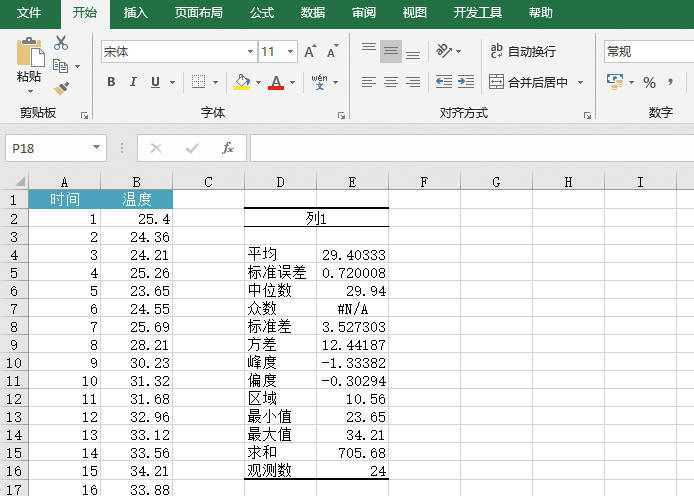
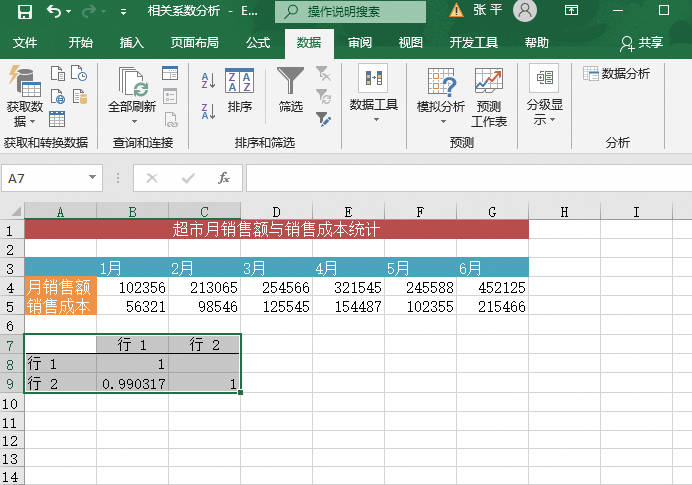
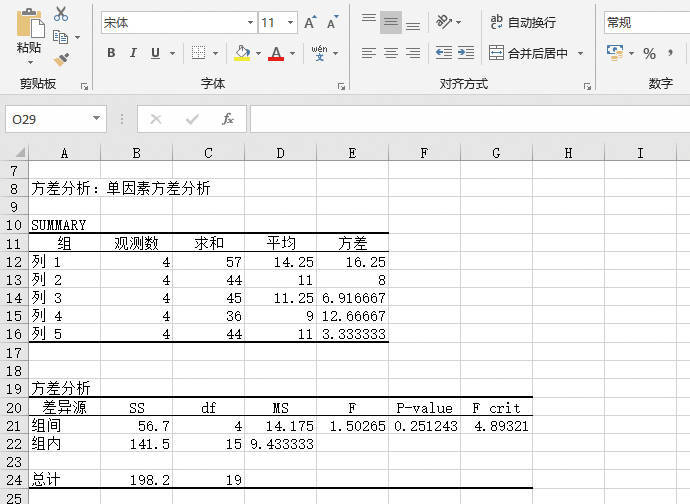
STEP05：此时，工作表中会显示“方差分析：单因素方差分析”的分析结果，如图22-29所示。由于F=1.50265<Fα=5.952544683，说明各地区每天的交通事故次数差异不显著。Fα为统计学固定值。

图22-28　“方差分析：单因素方差分析”对话框

图22-29　方差分析：单因素方差分析结果

包含重复的双因素方差分析

双因素方差分析用于观察两个因素的不同水平对所研究对象的影响是否存在明显的不同。根据是否考虑两个因素的交互作用，它又可以分为“包含重复的双因素方差分析”和“无重复的双因素方差分析”。本节首先介绍“包含重复的双因素方差分析”。

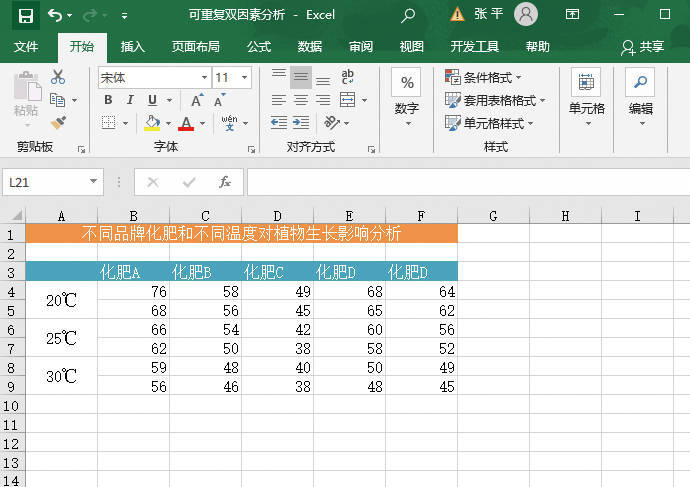
例如，在测量植物生长高度的实验中，共施用了5种不同品牌的化肥（A、B、C、D、E），同时植物处于不同温度（20℃、25℃、30℃）的环境中。对于每种化肥与每种温度的组合各统计两次，测定结果如图22-30所示，本例中的原始数据记录保存在“可重复双因素分析.xlsx”工作簿中。

图22-30　统计数据

使用“包含重复的双因素方差分析”可以检验：

1）施用不同化肥的植物高度是否取自相同的基础样本总体，此分析忽略温度。

2）处于不同温度环境中的植物高度是否取自相同的基础样本总体，此分析忽略所使用的化肥品牌。

无论是否考虑上述不同品牌化肥之间的差异的影响以及不同温度之间差异的影响，代表所有{化肥，温度}值对的样本都取自相同的样本总体。另一种假设是除了基于化肥或温度单个因素的差异带来的影响之外，特定的{化肥，温度}值对也会有影响。

下面通过实例介绍进行包含重复的双因素方差分析的具体操作步骤。

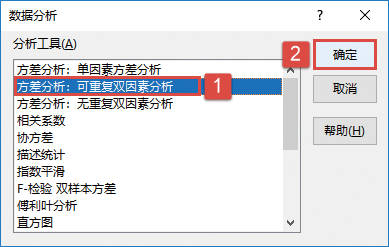
STEP01：选中工作表中的任意一个单元格，如B2单元格，切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮打开如图22-31所示的“数据分析”对话框，在“分析工具”列表框中选择“方差分析：可重复双因素分析”选项，然后单击“确定”按钮。

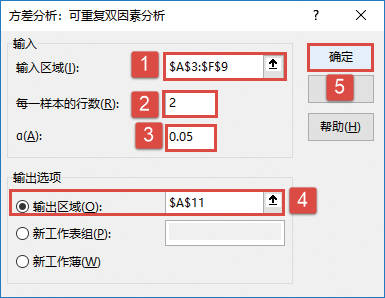
STEP02：随后会打开“方差分析：可重复双因素分析”对话框，在“输入”列表区域设置输入区域为“$A$3:$F$9”，在“每一样本的行数”文本框中输入“2”，设置α的值为“0.05”。然后在“输出选项”列表区域中单击选中“输出区域”单选按钮，并设置输出区域为“$A$11”单元格，最后单击“确定”按钮返回工作表，如图22-32所示。

图22-31　选择分析工具

图22-32　设置参数

在“每一样本的行数”框中输入包含在每个样本中的行数。每个样本必须包含同样的行数，因为每一行代表数据的一个副本。

STEP03：此时，工作表中会显示“方差分析：可重复双因素分析”的分析结果，如图22-33所示。

图22-33　可重复双因素方差分析结果

无重复的双因素方差分析

此分析工具可用于当数据像可重复双因素那样按照两个不同维度进行分类时的情况，只是此工具假设每一对值只有一个观察值，例如，在上面的示例中的每个{化肥，温度}值对。下面通过实例说明如何进行无重复的双因素方差分析。

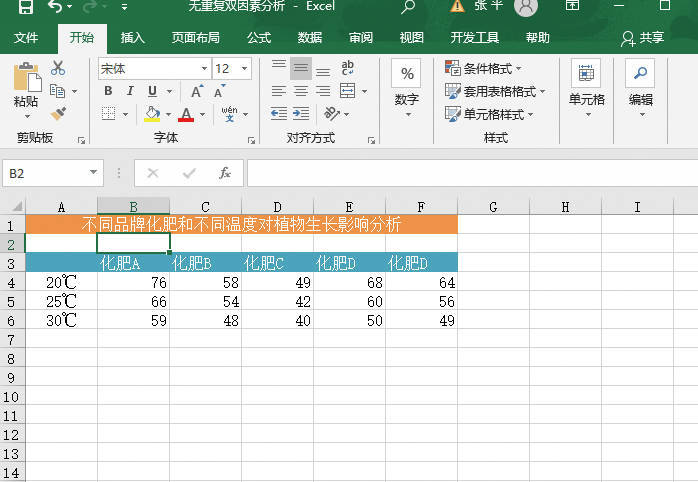
STEP01：打开“无重复双因素分析.xlsx”工作簿，将要处理的数据输入工作表中，本例中的原始数据如图22-34所示。

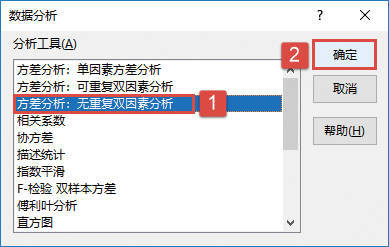
STEP02：选中工作表中的任意一个单元格，如B2单元格，切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮打开如图22-35所示的“数据分析”对话框。在“分析工具”列表框中选择“方差分析：无重复双因素分析”选项，然后单击“确定”按钮。

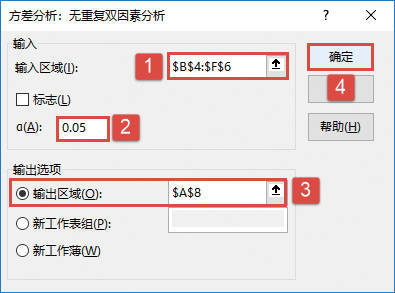
STEP03：随后会打开“方差分析：无重复双因素分析”对话框，在“输入”列表区域设置输入区域为“$B$4:$F$6”，设置α的值为“0.05”。然后在“输出选项”列表区域中单击选中“输出区域”单选按钮，并设置输出区域为“$A$8”单元格，最后单击“确定”按钮返回工作表，如图22-36所示。

图22-34　原始数据

图22-35　选择分析工具

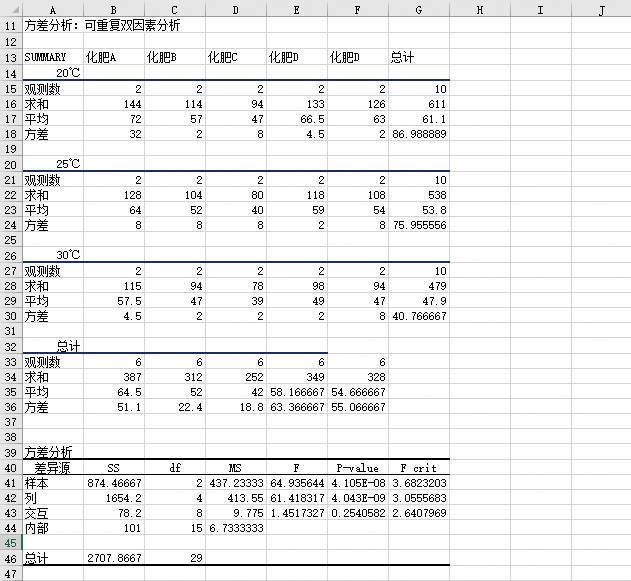
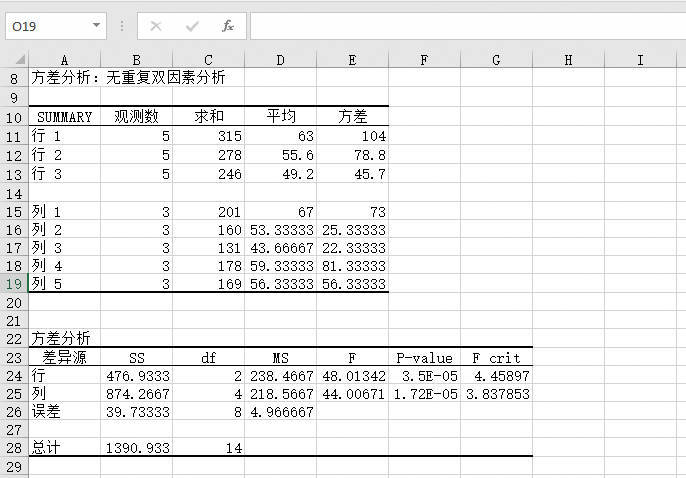
STEP04：此时，工作表中会显示“方差分析：无重复双因素分析”的分析结果，如图22-37所示。

图22-36　设置分析参数

图22-37　无重复双因素方差分析结果

要使用分析工具库，需要首先确保Excel中加载了分析工具库。如果在“数据”选项卡“分析”组中可以看到“数据分析”按钮，则已经加载了分析工具库，否则，必须先按以下步骤进行操作将其加载到Excel中。

STEP01：在工作表页面切换至“文件”选项卡，然后单击左侧导航栏中的“选项”标签打开“Excel选项”对话框，如图22-22所示。

图22-22　单击“选项“标签

STEP02：打开“Excel选项”对话框后，在左侧的导航栏中单击“加载项”标签，然后在“查看和管理Microsoft Office加载项”页面单击“管理”选择框右侧的下三角按钮，在展开的下拉列表中选择“Excel加载项”，单击“转到”按钮，如图22-23所示。

STEP03：随后会打开“加载项”对话框，在“可用加载宏”列表框中勾选“分析工具库”复选框，然后单击“确定”按钮即可完成分析工具库的加载，如图22-24所示。

图22-23　设置加载项

图22-24　勾选“分析工具库”复选框