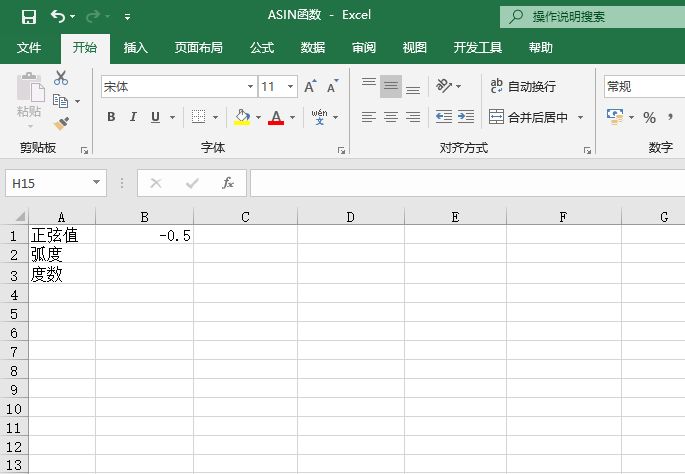
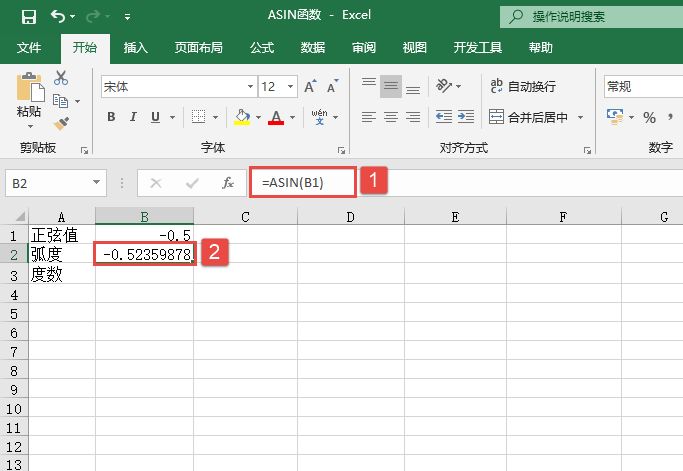
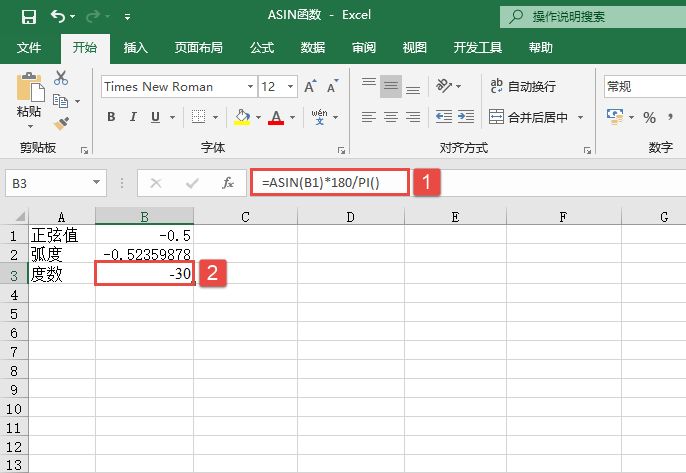
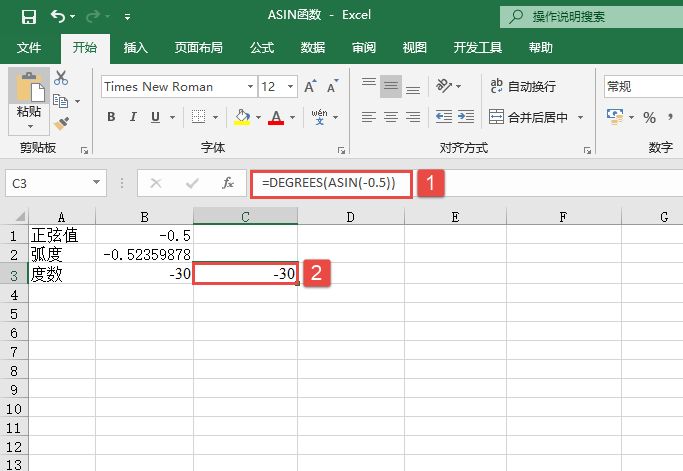
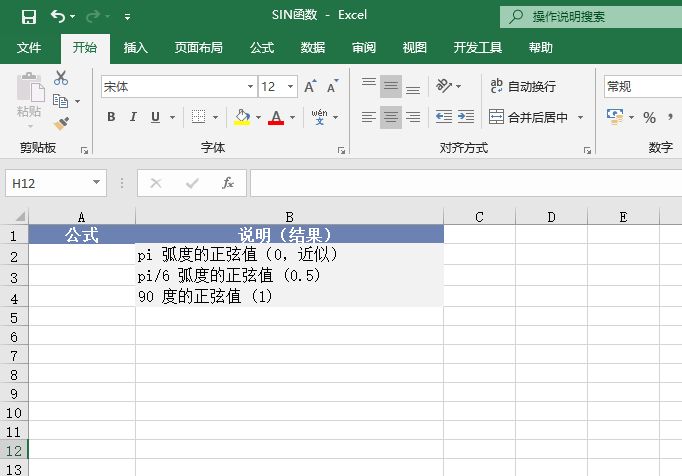
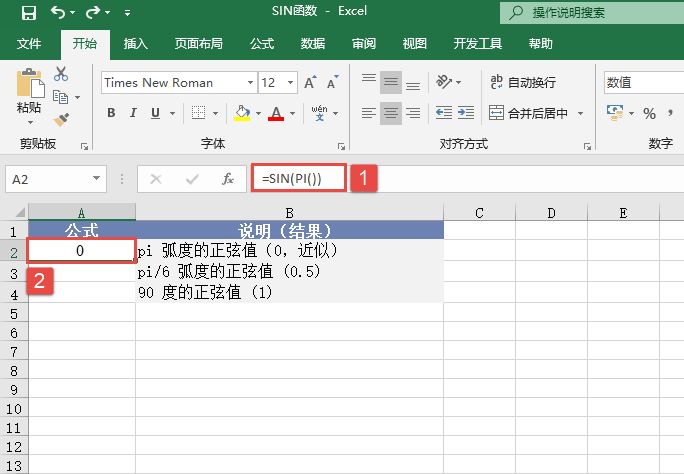
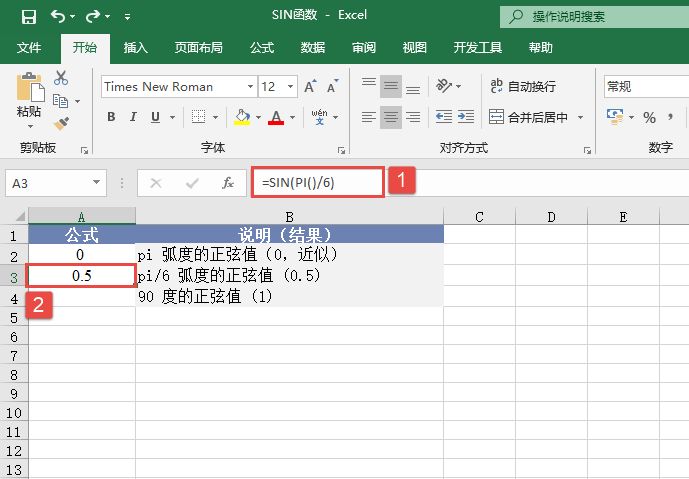
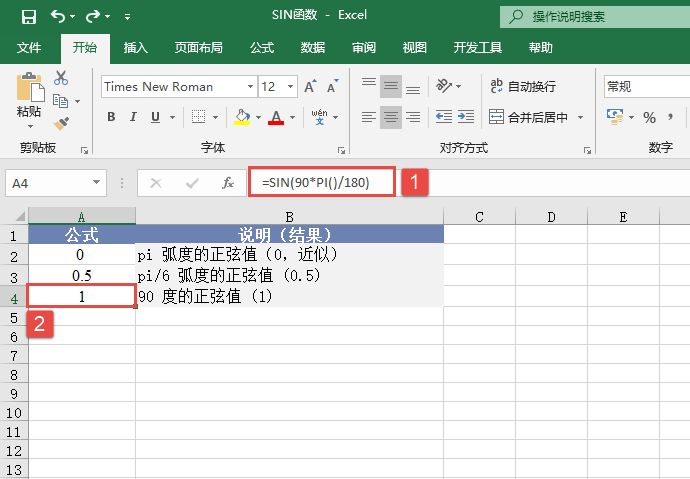
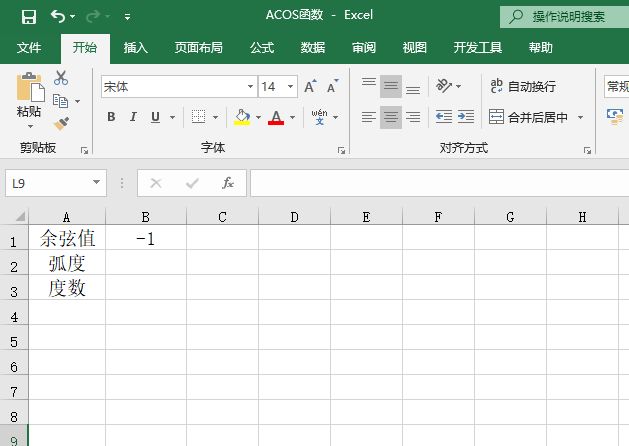
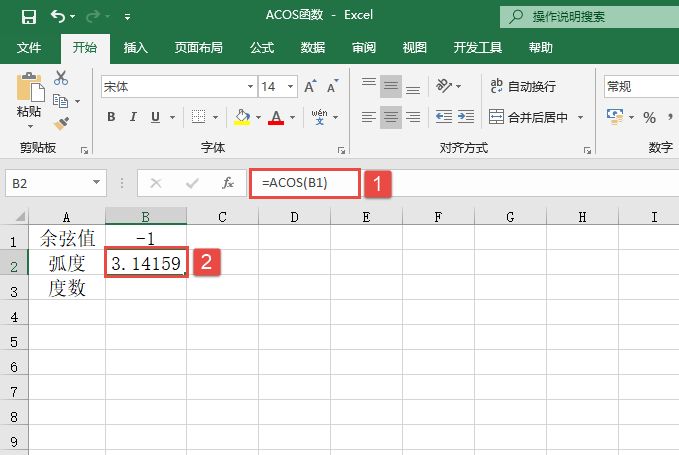
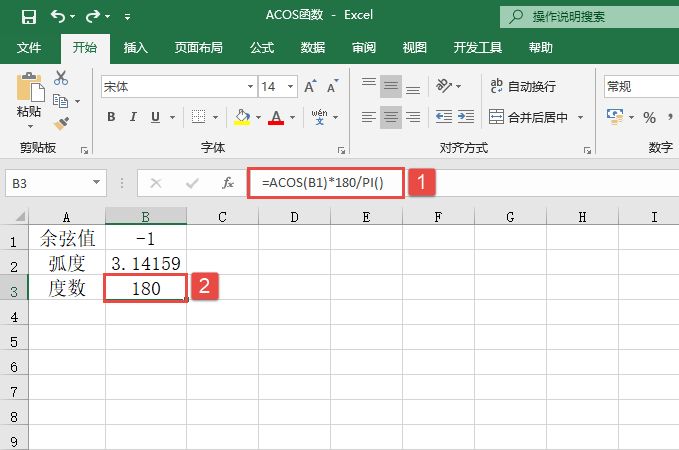
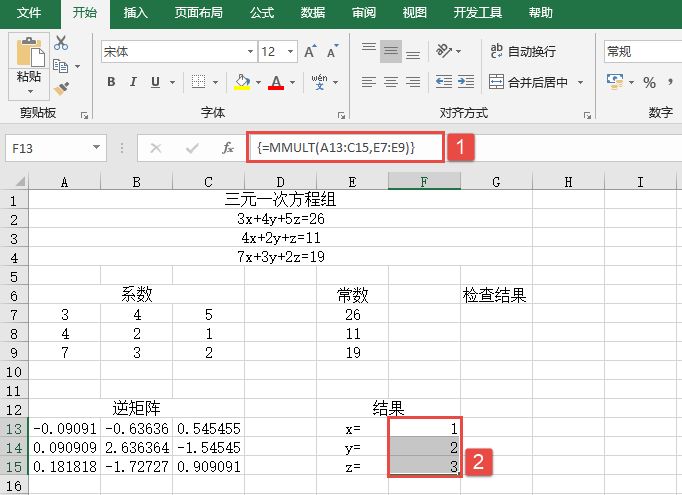
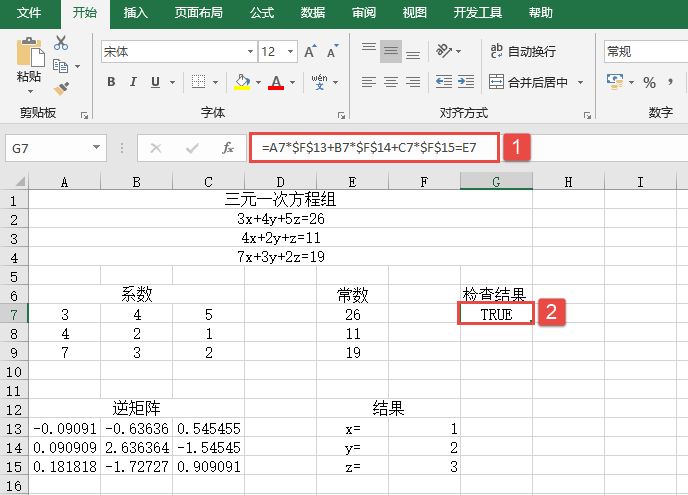
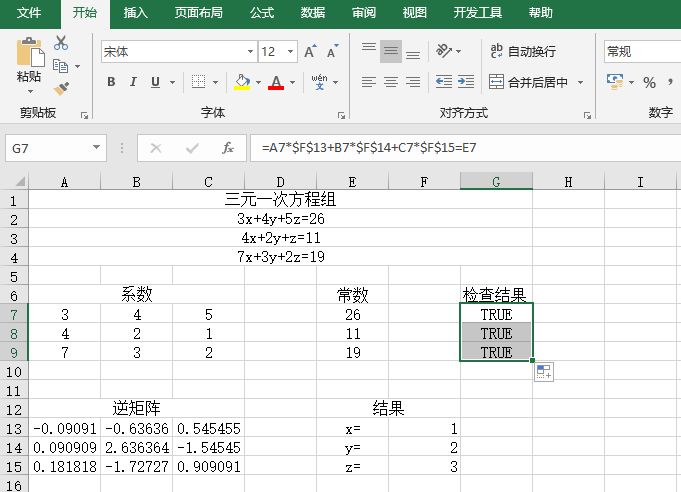
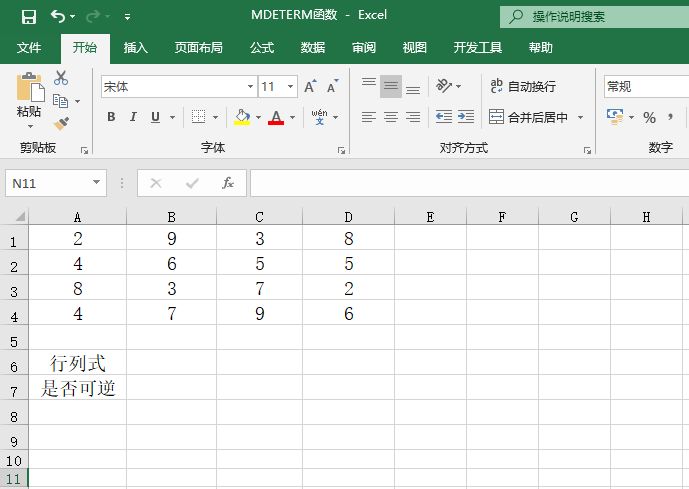
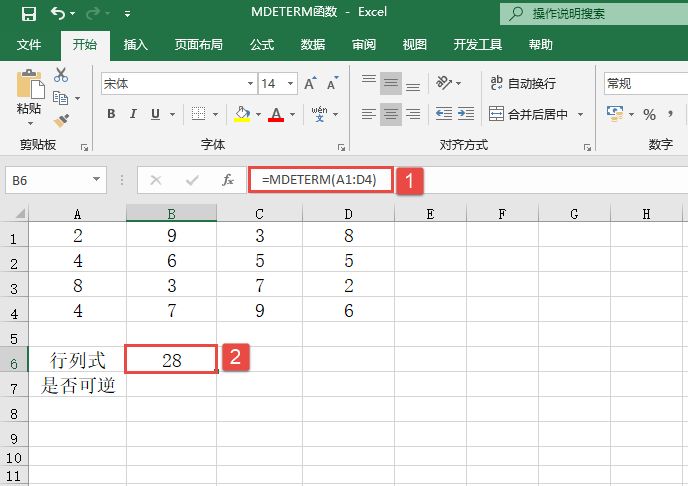
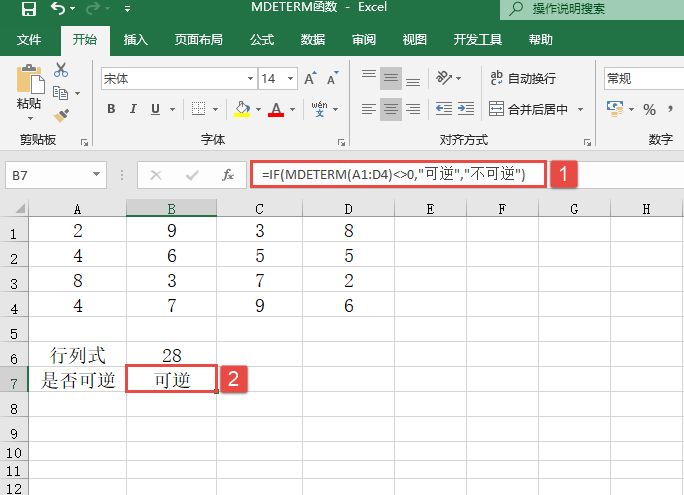
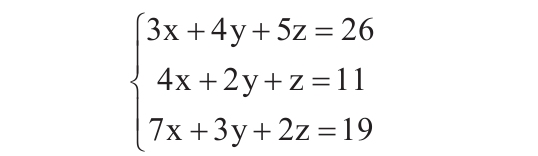某单位对员工的工资按不同级别计算个人所得税,按月扣除。个人所得税的计算公式是:个人所得税=应纳税所得额×适用税率-速算扣除数。而税后工资的计算公式是:税后工资=税前工资-个人所得税。不同级别的工资、薪金所得税率如表14-2所示。
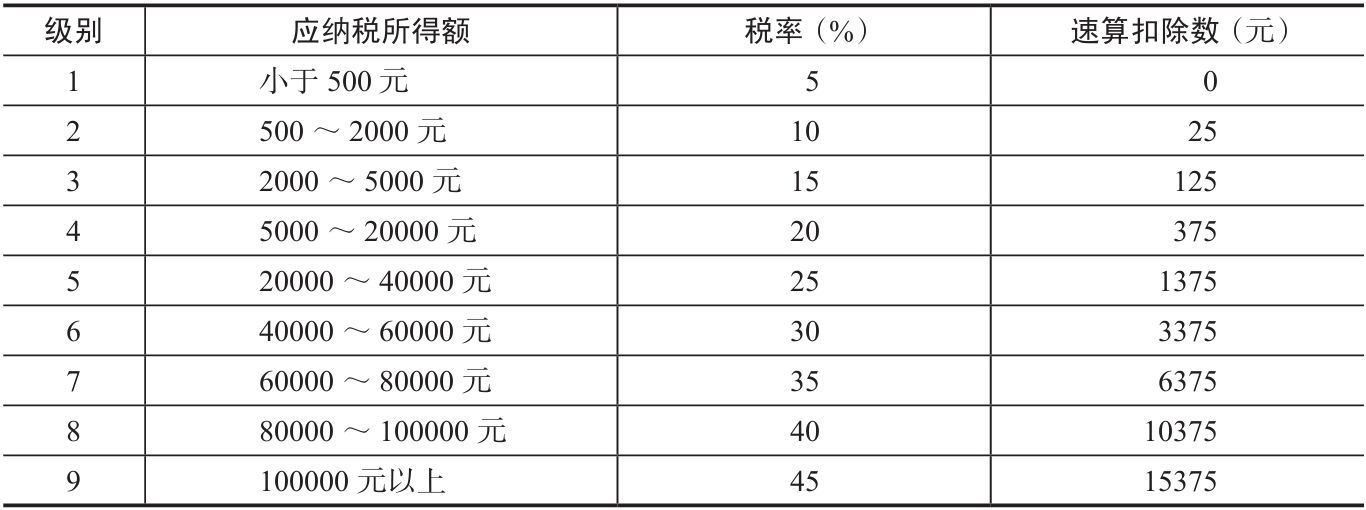
表14-2 工资、薪金所得税率表
下面通过实例说明如何计算个人所得税。打开“个人所得税.xlsx”工作簿,本例中的原始数据如图14-115所示。
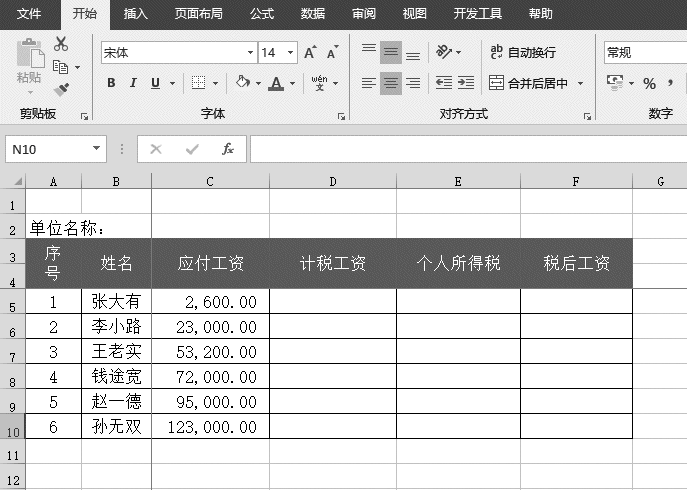
图14-115 原始数据
STEP01:选中D5单元格,在编辑栏中输入公式“=IF(C5>1600,C5-1600,0)”,按“Enter”键返回,即可计算出张大有的计税工资(假设计算个人所得税的基准金额为1600元,1600元以下不计个税),如图14-116所示。
以上公式判断C5单元格中的数值,如果大于1600,则用该数值减去基准金额1600元,得到应付个人所得税的金额,否则返回0,即不计税。
STEP02:选中D5单元格,利用填充柄工具向下复制公式至D10单元格,通过自动填充功能来计算其他员工的计税工资,结果如图14-117所示。
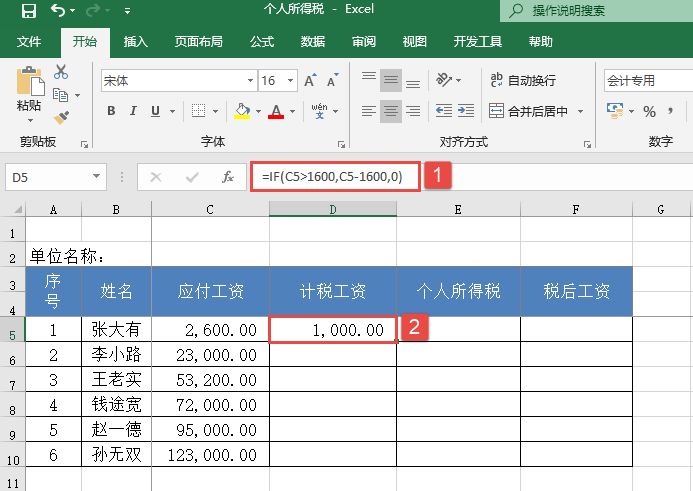
图14-116 计算张大有的计税工资
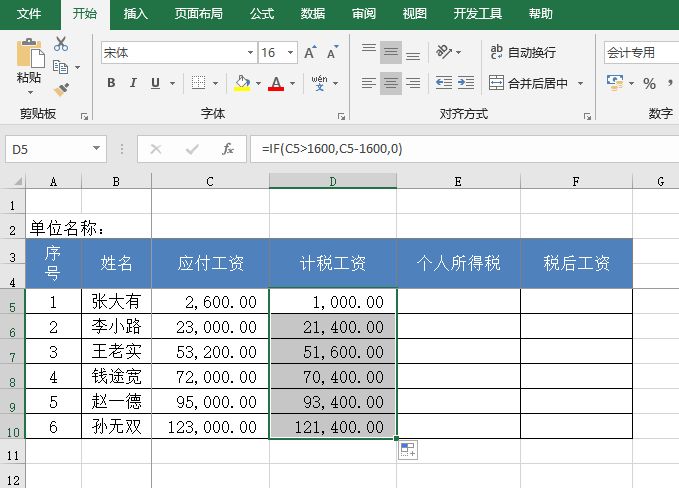
图14-117 计算其他员工的计税工资
STEP03:选中E5单元格,在编辑栏中输入公式“=IF(C5<>””,ROUND(IF(AND(C5>0,C5<=1600),0,SUM(IF((C5-1600>={0,500,2000,5000,20000,40000,60000,80000,100000})+(C5-1600<{500,2000,5000,20000,40000,60000,80000,100000,100000000000})=2,(C5-1600)*{0.05,0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45}-{0,25,125,375,1375,3375,6375,10375,15375},0))),2),””)”,按“Ctrl+Shift+Enter”组合键返回计算结果,同时,E5单元格中的公式会转换为数组公式,如图14-118所示。
在以上数组公式中,使用IF函数结合数组公式来根据不同的工资级别计算个人所得税。使用数组公式的优点是可以对一组或多组值进行多重计算。
STEP04:选中E5单元格,利用填充柄工具向下复制公式至E10单元格,通过自动填充功能来计算其他员工的个人所得说,结果如图14-119所示。
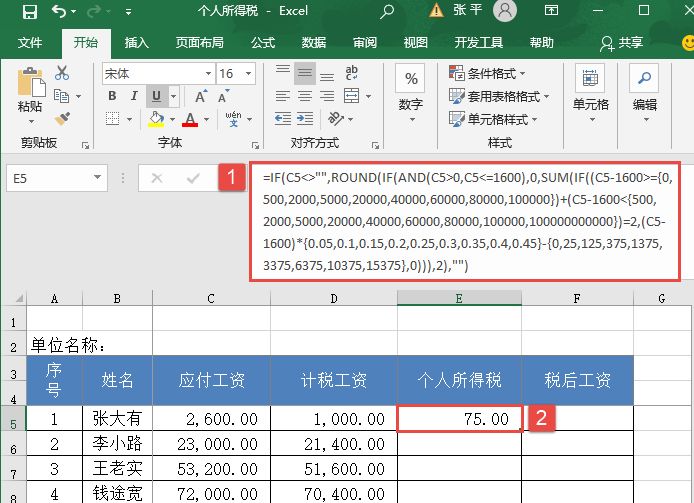
图14-118 计算张大有的个人所得说
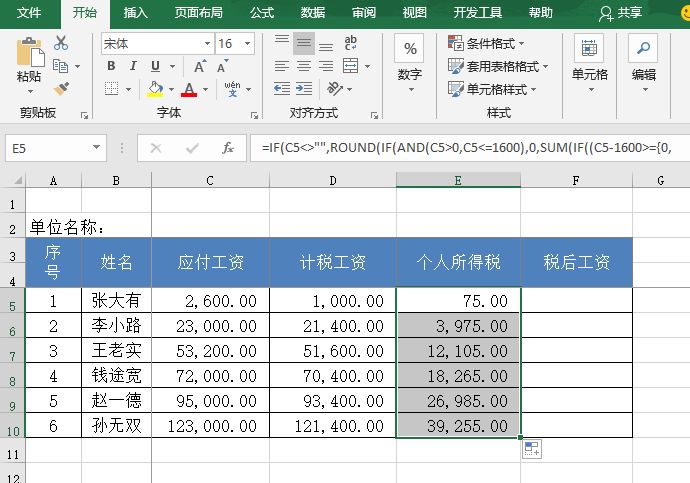
图14-119 计算个人所得说
STEP05:选中F5单元格,在编辑栏中输入公式“=C5-E5”,按“Enter”键返回,即可计算出张大有的税后工资,如图14-120所示。
STEP06:选中F5单元格,利用填充柄工具向下复制公式至F10单元格,通过自动填充功能来计算其他员工的税后工资,结果如图14-121所示。
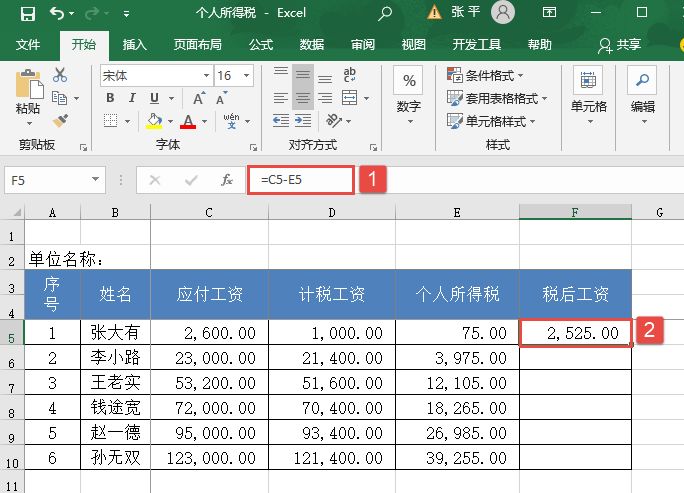
图14-120 计算张大有的税后工资
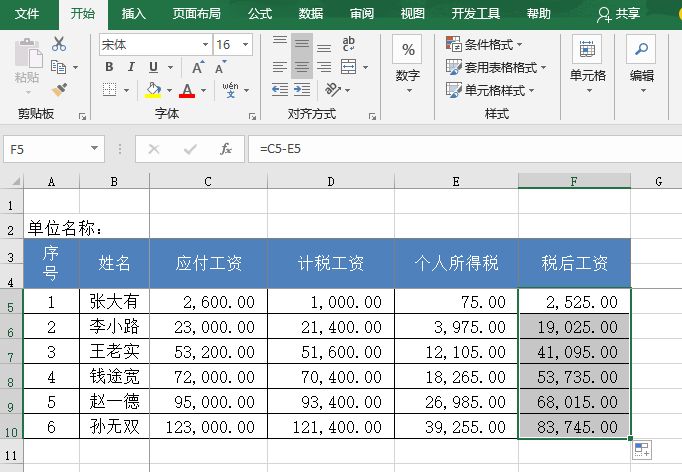
图14-121 税后工资计算结果