MINVERSE函数的功能是计算数组中存储的矩阵的逆矩阵。MMULT函数的功能是计算两个数组的矩阵乘积,结果矩阵的行数与参数array1的行数相同,矩阵的列数与参数array2的列数相同。两函数的语法分别如下:
MINVERSE(array) MMULT(array1,array2)
其中,array参数是行数和列数相等的数值数组。参数array1、array2是要进行矩阵乘法运算的两个数组,可以是单元格区域、数组常量或引用。
在MINVERSE函数中,提到了一个概念——逆矩阵。如图14-78所示的是计算二阶方阵逆矩阵的示例。假设A1:B2中包含以字母a、b、c和d表示的4个任意的数,则该表表示矩阵A1:B2的逆矩阵。
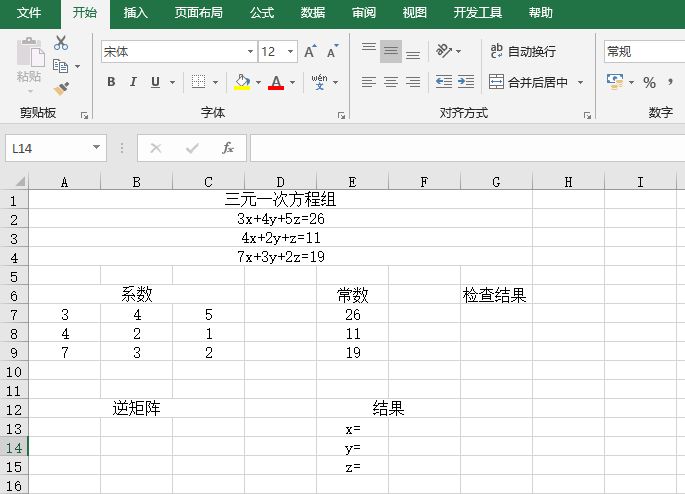
要求使用MINVERSE函数和MMULT函数,求下面的三元一次方程组的解。
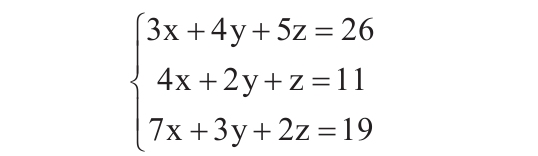
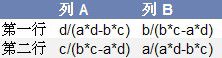
图14-78 矩阵A1:B2的逆矩阵
打开“求解方程.xlsx”工作簿,本例的原始数据如图14-79所示。
STEP01:选中A13:C15单元格区域,在编辑栏中输入公式“=MINVERSE(A7:C9)”,然后按“Ctrl+Shift+Enter”组合键返回,即可计算出系数矩阵的逆矩阵,结果如图14-80所示。
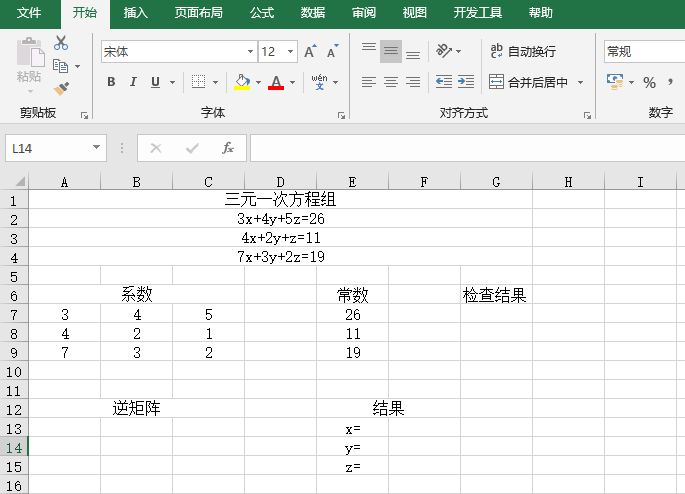
图14-79 原始数据
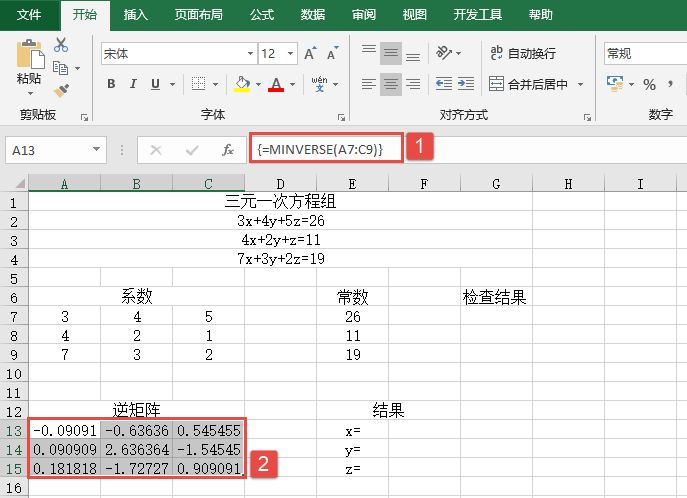
图14-80 求解系数矩阵的逆矩阵
STEP02:选中F13:F15单元格区域,在编辑栏中输入公式“=MMULT(A13:C15,E7:E9)”,然后按“Ctrl+Shift+Enter”组合键返回,即可计算出方程组的数值矩阵,即方程组的解,如图14-81所示。
STEP03:选中G7单元格,在编辑栏中输入公式“=A7*$F$13+B7*$F$14+C7*$F$15=E7”,用来检查方程组的解是否满足第1个方程,按“Enter”键即可返回检查结果,如图14-82所示。
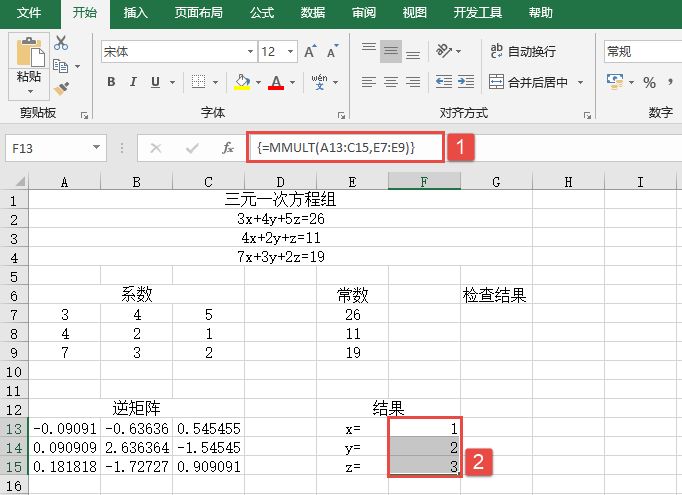
图14-81 求三元一次方程组的数值矩阵
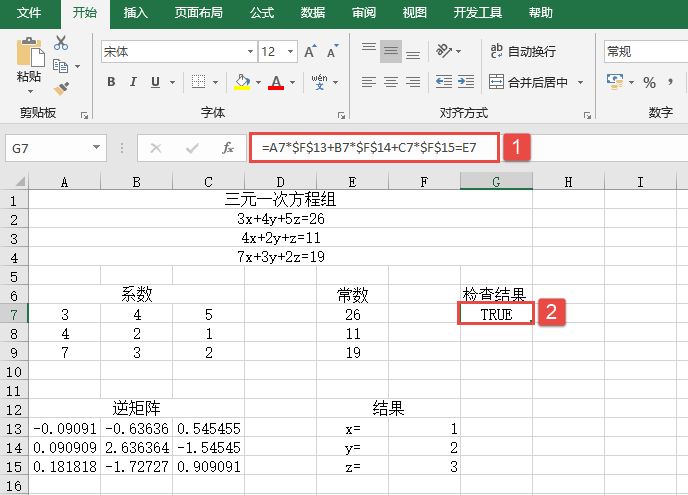
图14-82 检查方程组的解是否正确
STEP04:选中G7单元格,利用填充柄工具向下复制公式至G9单元格,通过自动填充功能来检查下面的两个方程是否满足,最终检查结果如图14-83所示。
与求行列式的值一样,求解逆矩阵常被用于求解多元联立方程组。所以可以将MINVERSE函数和MMULT函数结合在一起,求解一个方程组。
在MINVERSE函数中,array参数可以是单元格区域,或单元格区域和数组常量的名称。如果array参数中的单元格为空、包含文字或是行和列的数目不相等,则函数MINVERSE将返回错误值“#VALUE!”。对于一些不能求逆的矩阵,MINVERSE函数将返回错误值“#NUM!”。不能求逆的矩阵的行列式值为零。
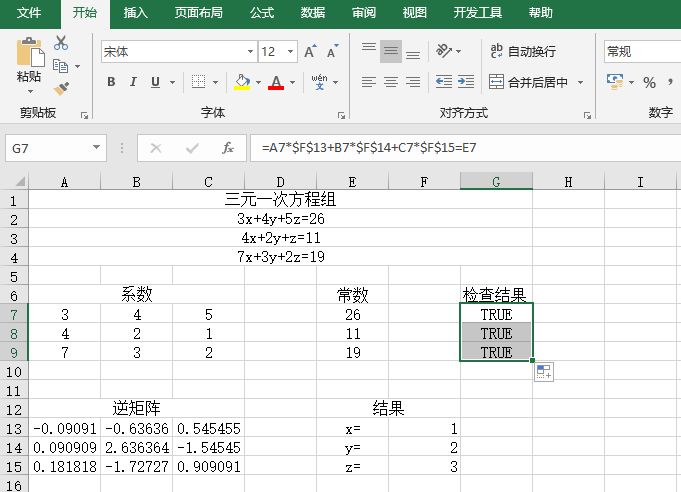
图14-83 检查方程结果
在MMULT函数中,array1参数的列数与array2参数的行数必须相同,而且两个数组中都只能包含数值。如果array1参数和array2参数中的单元格为空、包含文字或是行和列的数目不相等,MMULT函数将返回错误值“#VALUE!”。