幂与平方计算

Excel 计算e的n次幂：EXP函数

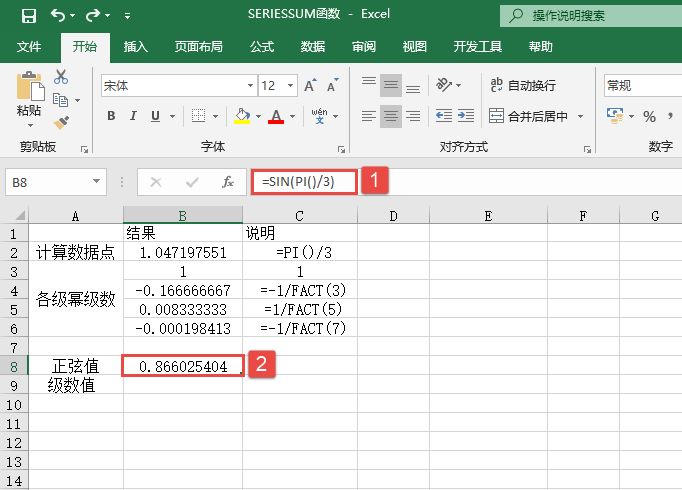
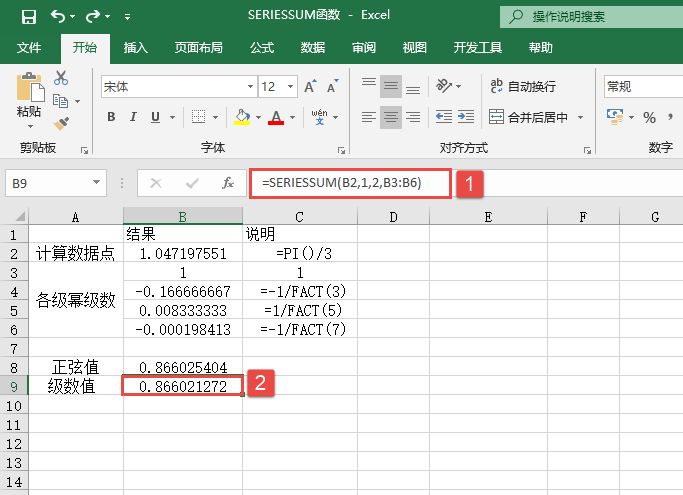
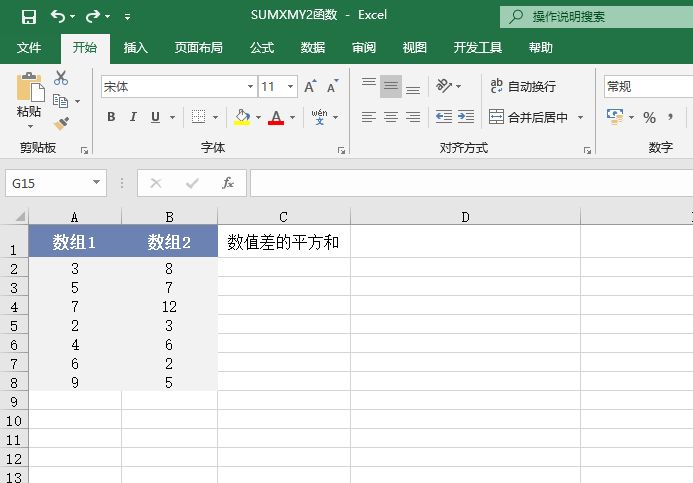
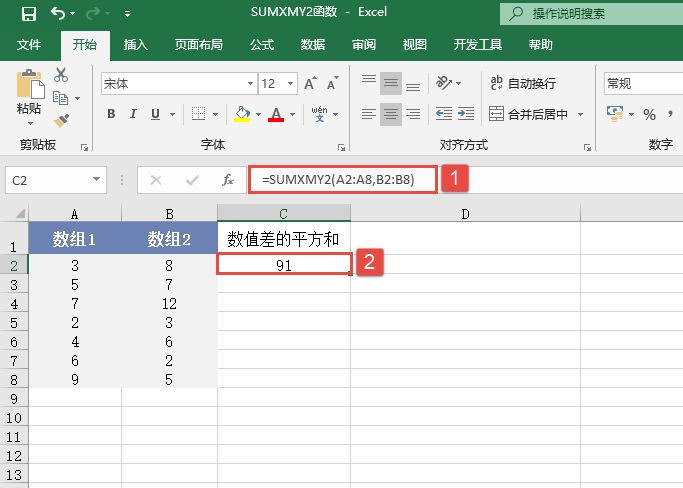
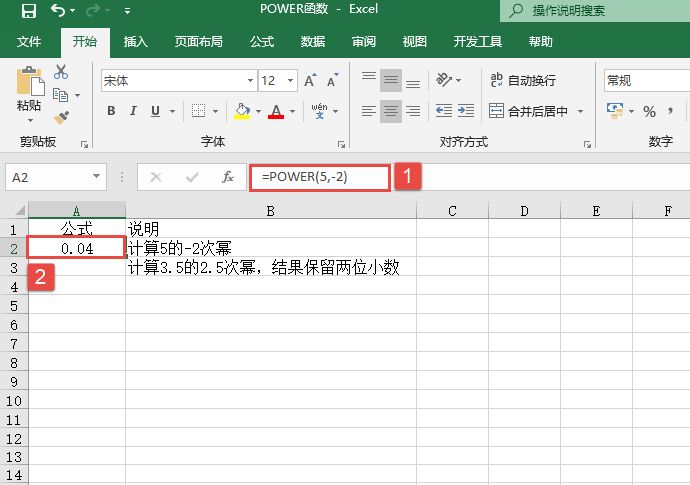
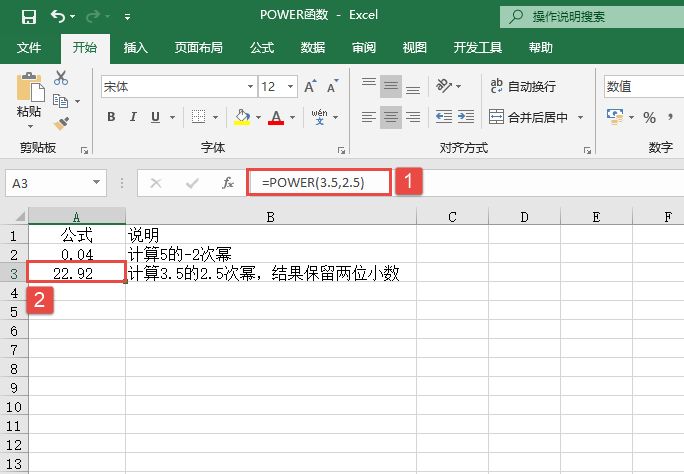
EXP函数的功能是计算e的n次幂。EXP函数的语法如下：

EXP(number)

其中，number参数为应用于底数e的指数。常数e等于2.71828182845904，是自然对数的底数。下面通过实例详细讲解该函数的使用方法与技巧。

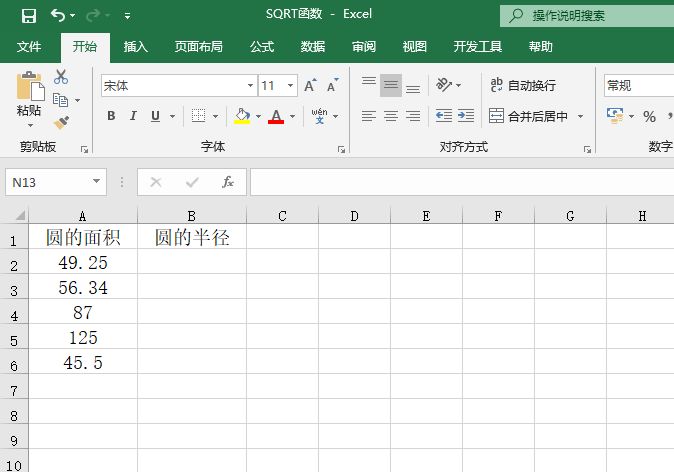
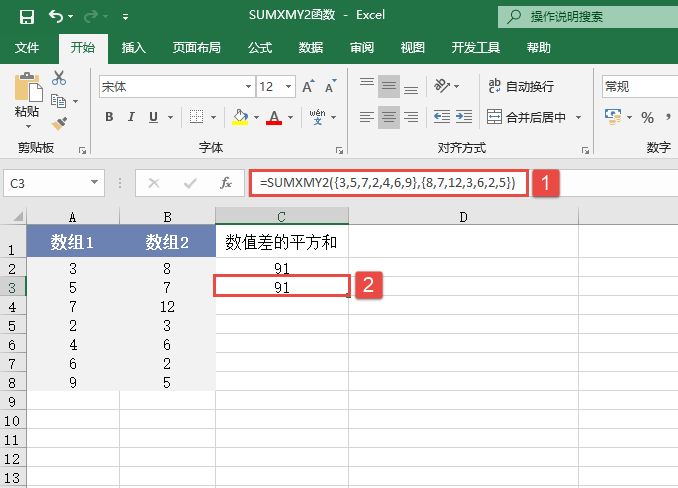
已知某函数表达式y=ex，现求解x的取值在-5～5之间的函数曲线。打开“EXP函数.xlsx”工作簿，本例中的原始数据如图14-70所示。具体求解步骤如下。

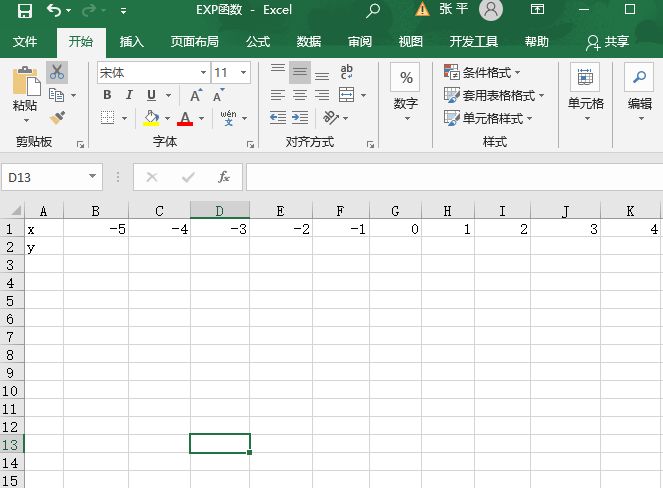
图14-70　原始数据

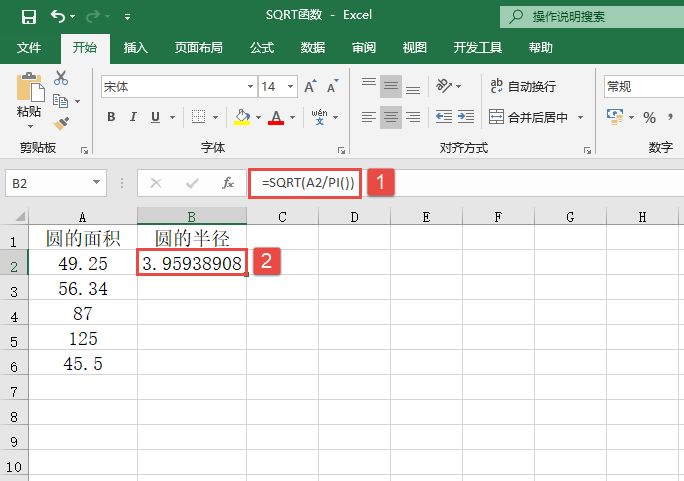
STEP01：选中B2单元格，在编辑栏中输入公式“=EXP(B1)”，然后按“Enter”键返回，即可计算出y=e-5的值，结果如图14-71所示。

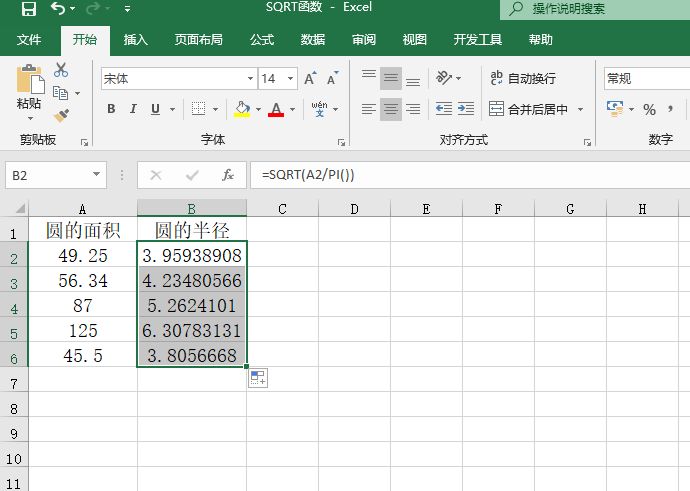
STEP02：选中B2单元格，利用填充柄工具向右复制公式至L2单元格，通过自动填充功能来计算出其他的函数值，如图14-72所示。

STEP03：切换至“插入”选项卡，在“图表”组中单击“插入散点图或气泡图”下三角按钮，在展开的下拉列表中选择“带平滑线的散点图”选项，如图14-73所示。随后，工作表中会自动插入如图14-74所示的散点图，即-5～5之间的函数曲线。

用EXP函数可以计算不同参数的指数数值。e=2.71828182…是微积分中的两个常用极限之一，它有一些特殊的性质，在数学、物理等学科中有广泛应用。在使用EXP函数时，如果要计算以其他常数为底的幂，必须使用指数操作符（^）。EXP函数是计算自然对数的LN函数的反函数。

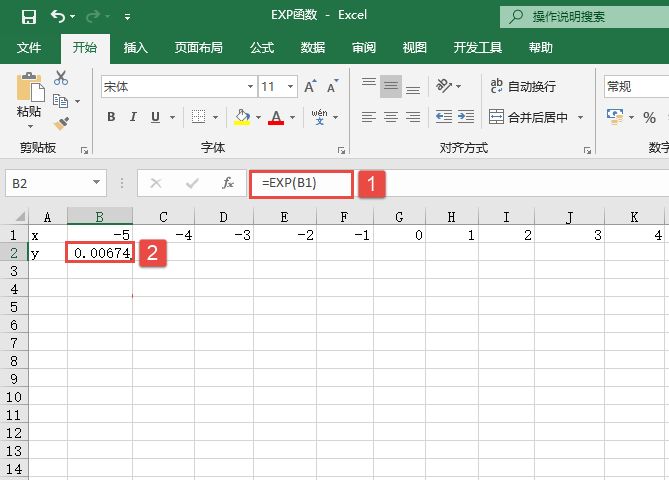
图14-71　计算B1单元格对应的y值

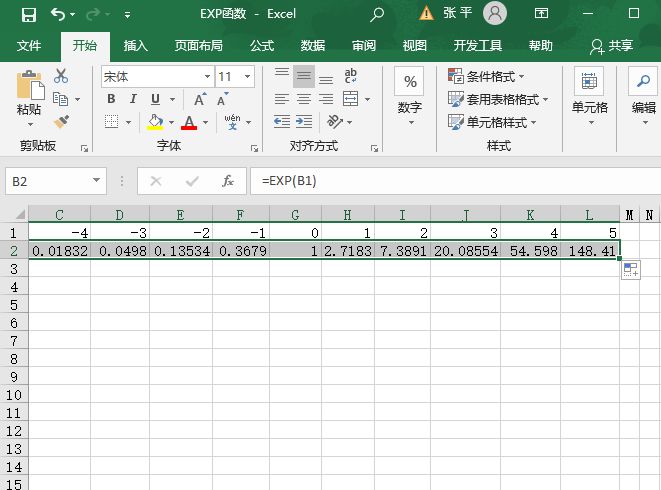
图14-72　计算函数值

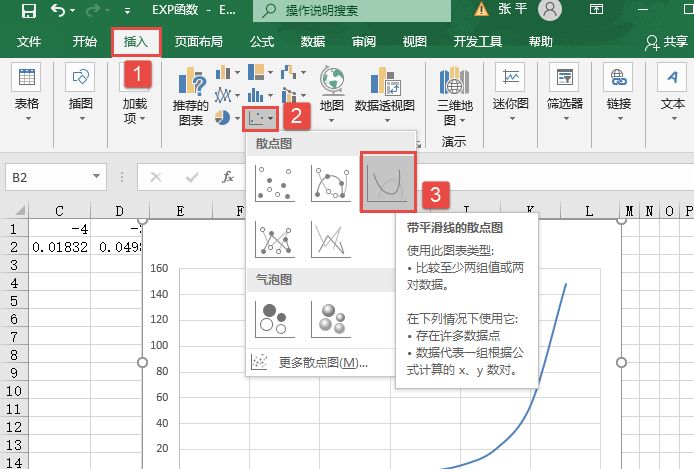
图14-73　选择散点图类型

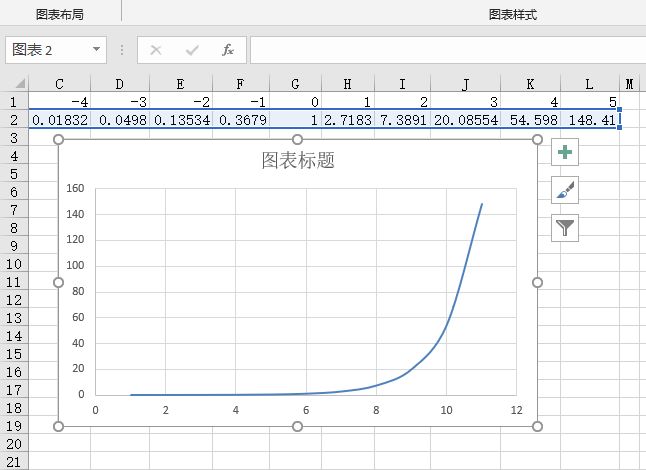
图14-74　生成函数曲线

Excel 计算正数平方根：SQRT函数图解

SQRT函数的功能是计算正数的平方根。其语法如下：

SQRT(number)

其中，number参数为要计算平方根的数。下面通过实例详细讲解该函数的使用方法与技巧。

打开“SQRT函数.xlsx”工作簿，本例中的原始数据如图14-67所示。已知圆的面积，求圆的半径。具体求解步骤如下。

图14-67　原始数据

STEP01：选中B2单元格，在编辑栏中输入公式“=SQRT(A2/PI())”，然后按“Enter”键返回，即可计算出第1个圆的半径，结果如图14-68所示。

STEP02：选中B2单元格，利用填充柄工具向下复制公式至B6单元格，通过自动填充功能来计算其他圆的半径，如图14-69所示。

图14-68　计算第一个圆的半径

图14-69　计算所有圆的半径

对SQRT函数来说，如果number参数为负值，SQRT函数返回错误值“#NUM!”。

Excel 计算幂级数之和：SERIESSUM函数

SERIESSUM函数的功能是计算基于幂级数展开式的幂级数之和。许多函数可由幂级数展开式近似地得到。其语法如下：

SERIESSUM(x,n,m,coeffi cients)

其中，x参数为幂级数的输入值；参数n为参数x的首项乘幂；m参数为级数中每一项的乘幂n的步长增加值；coefficients参数为一系列与参数x各级乘幂相乘的系数，它的数目决定了幂级数的项数，如果参数coefficients中有3个值，幂级数中将有3项。

在该函数的功能提到一个概念——幂级数。幂级数形式上是个无穷多项式，通常依变量x的升幂顺序来表示。幂级数是微积分中的重要内容，许多重要的函数可以幂级数表示，而幂级数全体也代表了相当广泛的函数类别。下面通过实例详细讲解该函数的使用方法与技巧。

根据幂级数展开式求解函数y=sinx在x=π/3的近似函数值，并将该近似值与直接求解的结果进行比较，其中sinx的级数展开式为：sinx=x-x3/3!+x5/5!-x7/7!+……。打开“SERIESSUM函数.xlsx”工作簿，本例的原始数据如图14-64所示。具体操作步骤如下。

图14-64　原始数据

STEP01：选中B8单元格，在编辑栏中输入公式“=SIN(PI()/3)”，然后按“Enter”键返回，即可计算出y=sinx在x=π/3的准确结果，如图14-65所示。

STEP02：选中B9单元格，在编辑栏中输入公式“=SERIESSUM(B2,1,2,B3:B6)”，然后按“Enter”键返回，即可计算出y=sinx在x=π/3的级数展开数值，如图14-66所示。

图14-65　计算y=sinx在x=π/3的准确结果

图14-66　计算函数的级数值

SERIESSUM函数主要用来求解函数在某一点的近似值。对该函数来说，如果任一参数为非数值型，SERIESSUM函数将会返回错误值“#VALUE!”。

Excel 计算数组差值的平方和：SUMXMY2函数

SUMXMY2函数的功能是，计算两数组中对应数值之差的平方和。其语法如下：

SUMXMY2(array_x,array_y)

其中参数array_x表示第1个数组或数值区域，参数array_y表示第2个数组或数值区域。下面通过实例详细讲解该函数的使用方法与技巧。

打开“SUMXMY2函数.xlsx”工作簿，本例中的原始数据如图14-61所示。该工作表中记录了两组数据，要求利用SUMXMY2函数求解两组数据的对应差值的平方和。具体的操作步骤如下。

图14-61　原始数据

STEP01：选中C2单元格，在编辑栏中输入公式“=SUMXMY2(A2:A8,B2:B8)”，然后按“Enter”键返回，即可计算出数值区域1和数值区域2的数值之差的平方和，结果如图14-62所示。

STEP02：选中C3单元格，在编辑栏中输入公式“=SUMXMY2({3,5,7,2,4,6,9},{8,7,12,3,6,2,5})”，然后按“Enter”键返回，即可计算出数组1和数组2的数值之差的平方和，结果如图14-63所示。可以看出这两种方法求出的结果相同。

图14-62　计算数值区域差值的平方和

图14-63　计算数值差的平方和

对SUMXMY2函数来说，参数可以是数字、包含数字的名称、数组或引用。如果数组或引用参数包含文本、逻辑值或空白单元格，则这些值将被忽略；但包含零值的单元格将计算在内。如果参数array_x和参数array y的元素数目不同，SUMXMY2函数将返回错误值“#N/A”。

Excel 计算参数平方和：SUMSQ函数

SUMSQ函数的功能是计算参数的平方和。其语法如下：

SUMSQ(number1,number2, ...)

其中，参数number、number2……为1～255个需要求平方和的参数，也可以使用数组或对数组的引用来代替以逗号分隔的参数。下面通过实例详细讲解该函数的使用方法与技巧。

打开“SUMSQ函数.xlsx”工作簿，本例中的原始数据如图14-59所示。该工作表中记录了一组数据，要求利用SUMSQ函数求这组数据的平方和。具体的操作步骤如下。

选中B2单元格，在编辑栏中输入公式“=SUMSQ(B1:F1)”，然后按“Enter”键返回即可计算出以上各数据的平方和，结果如图14-60所示。

图14-59　原始数据

图14-60　计算结果

Excel 计算给定数字的乘幂：POWER函数

POWER函数的功能是，计算给定数字的乘幂。其语法如下：

POWER(number,power)

其中，number参数为底数，可以为任意实数，power参数为指数，底数按该指数次幂乘方。下面通过实例详细讲解该函数的使用方法与技巧。

打开“POWER函数.xlsx”工作簿，本例中要求计算的数值说明如图14-56所示。

图14-56　原始数据

STEP01：选中A2单元格，在编辑栏中输入公式“=POWER(5,-2)”，然后按“Enter”键返回即可计算出5的-2次幂，结果如图14-57所示。

STEP02：选中A3单元格，在编辑栏中输入公式“=POWER(3.5,2.5)”，然后按“Enter”键返回即可计算出3.5的2.5次幂，结果如图14-58所示。

图14-57　计算5的-2次幂

图14-58　计算14.6的2.5次幂

POWER函数主要用来计算不同数据的乘幂。可以用“^”运算符代替函数POWER函数来表示对底数乘方的幂次，例如7^2的结果等同于公式“=POWER(7,2)”的结果。