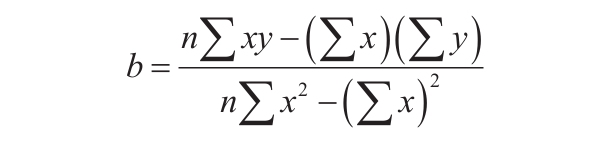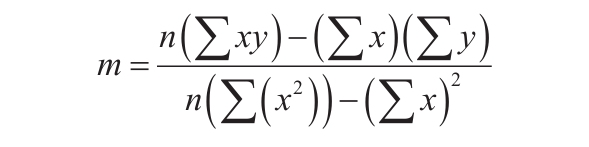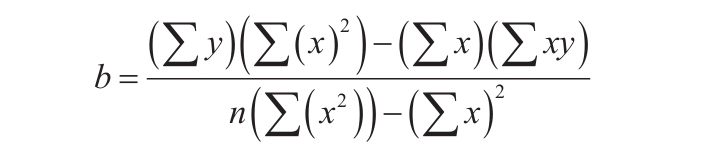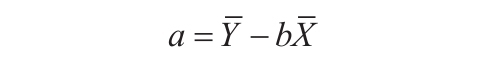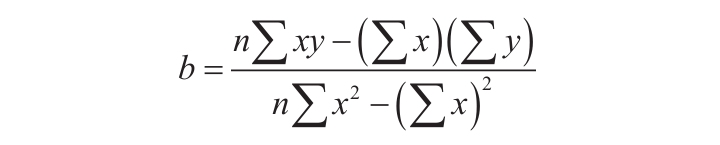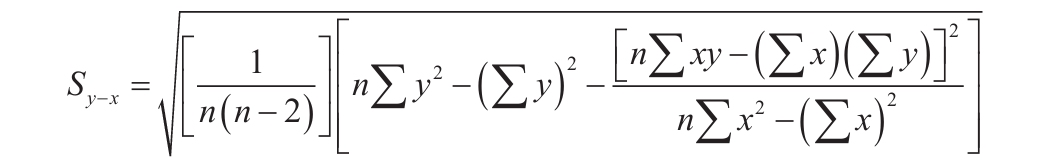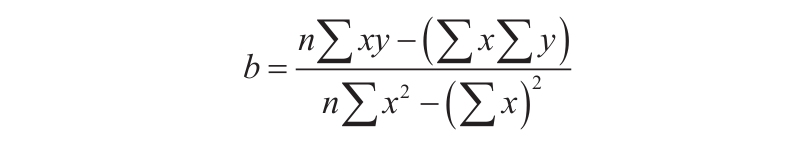LINEST函数用于使用最小二乘法对已知数据进行最佳直线拟合,然后返回描述此直线的数组。也可以将LINEST与其他函数结合,以便计算未知参数中其他类型的线性模型的统计值,包括多项式、对数、指数和幂级数。因为此函数返回数值数组,所以必须以数组公式的形式输入。LINEST函数的语法如下:
LINEST(known_y's,known_x's,const,stats)
其中,known_y’s参数是关系表达式y=mx+b中已知的y值集合。如果数组known_y’s在单独一列中,则known_x’s的每一列被视为一个独立的变量。如果数组known_y’s在单独一行中,则known_x’s的每一行被视为一个独立的变量。
known_x’s参数是关系表达式y=mx+b中已知的可选x值集合。数组known_x’s可以包含一组或多组变量。如果仅使用一个变量,那么只要known_x’s参数和known_y’s参数具有相同的维数,则它们可以是任何形状的区域。如果用到多个变量,则known_y’s参数必须为向量(即必须为一行或一列)。如果省略known_x’s参数,则假设该数组为{1,2,3,…},其大小与known_y’s参数相同。
const参数为一逻辑值,用于指定是否将常量b强制设为0。如果const参数为TRUE或省略,b将按正常计算。如果const参数为FALSE,b将被设为0,并同时调整m值使y=mx。stats参数为一逻辑值,指定是否返回附加回归统计值。如果stats参数为TRUE,则LINEST函数返回附加回归统计值,这时返回的数组为{mn,mn-1,…,m1,b;sen,sen-1,…,se1,seb;r2,sey;F,df;ssreg,ssresid}。如果stats参数为FALSE或省略,LINEST函数只返回系数m和常量b。
直线的公式为:y=mx+b或y=m1x1+m2x2+…+b(如果有多个区域的x值)。
其中,因变量y是自变量x的函数值。m值是与每个x值相对应的系数,b为常量。注意y、x和m可以是向量。LINEST函数返回的数组为{mn,mn-1,…,m1,b}。LINEST函数还可返回附加回归统计值。
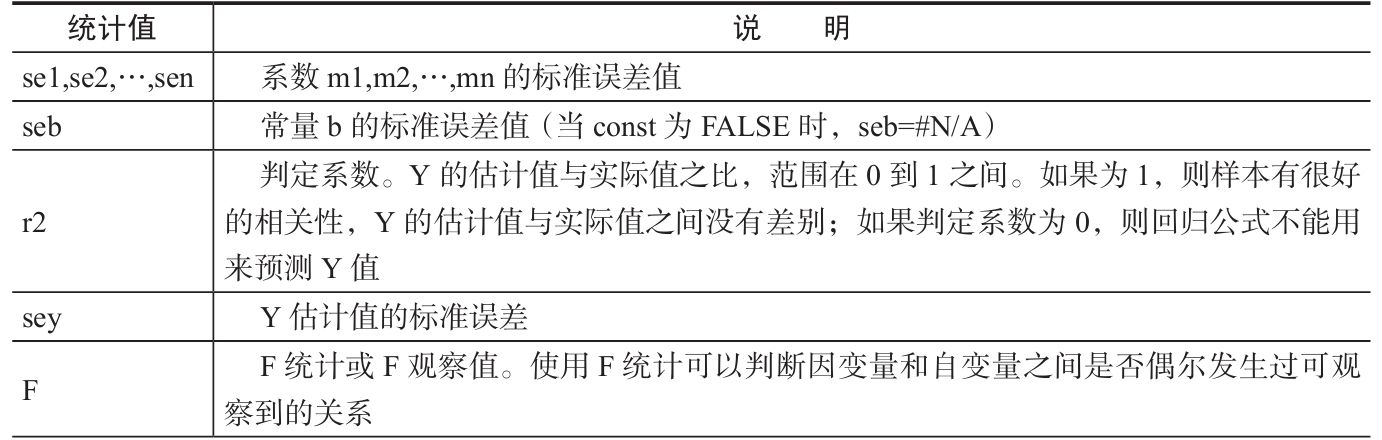
附加回归统计值如表18-1所示。
表18-1 附加回归统计值
打开“LINEST函数.xlsx”工作簿,切换至“Sheet1”工作表,本例中的原始数据如图18-72所示。已知某公司1月~6月的产品销售额,要求估算第8个月的销售值。具体的操作步骤如下。
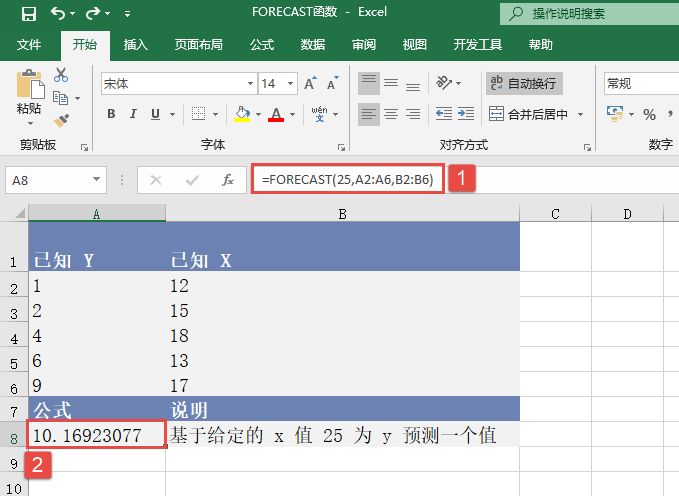
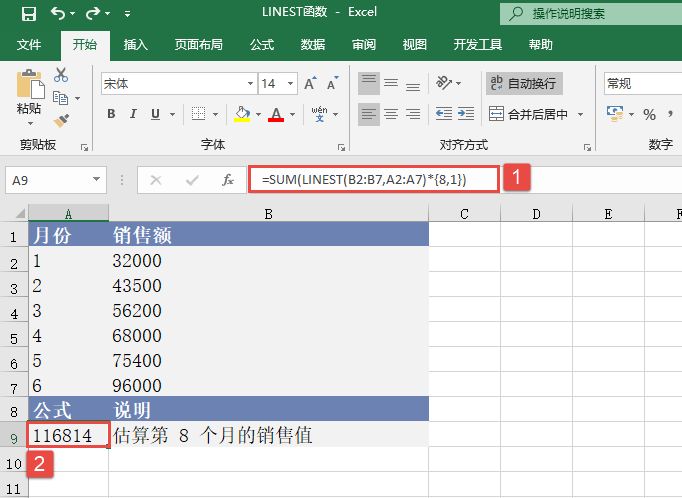
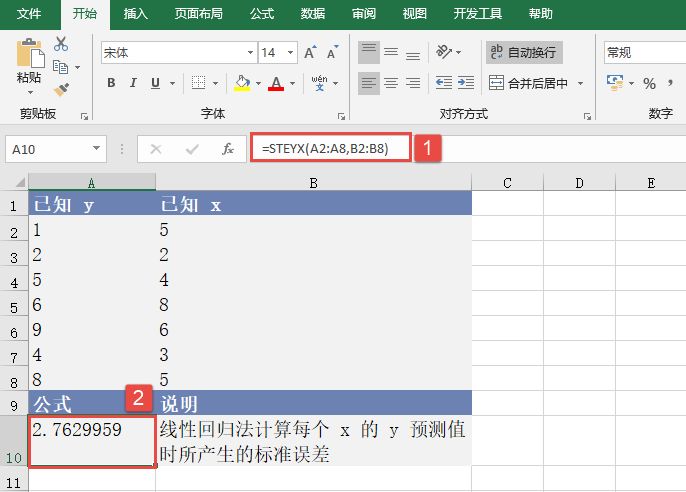
选中A9单元格,在编辑栏中输入公式“=SUM(LINEST(B2:B7,A2:A7)*{8,1})”,用于估算第8个月的销售值,输入完成后按“Enter”键返回计算结果,如图18-73所示。
图18-72 原始数据
图18-73 估算销售值
需要注意的有以下几点:
1)可以使用斜率和y轴截距描述任何直线。
斜率(m)通常记为m,如果需要计算斜率,则选取直线上的两点,(x1,y1)和(x2,y2);斜率等于(y2-y1)/(x2-x1)。
Y轴截距(b)通常记为b,直线的y轴的截距为直线通过y轴时与y轴交点的数值。
直线的公式为y=mx+b。如果知道了m和b的值,将y或x的值代入公式就可计算出直线上的任意一点。还可以使用TREND函数计算。
2)当只有一个自变量x时,可直接利用下面公式得到斜率和y轴截距值。
斜率:
=INDEX(LINEST(known_y's,known_x's),1)
Y轴截距:
=INDEX(LINEST(known_y's,known_x's),2)
3)数据的离散程度决定了LINEST函数计算的精确度。数据越接近线性,LINEST模型就越精确。LINEST函数使用最小二乘法来判定最适合数据的模型。当只有一个自变量x时,m和b是根据下面的公式计算出的。
其中x和y是样本平均值,例如x=AVERAGE(knownx’s)和y=AVERAGE(known_y’s)。
4)直线和曲线函数LINEST和LOGEST可用来计算与给定数据拟合程度最高的直线或指数曲线,但需要判断两者中哪一个更适合数据。可以用函数TREND(known_y’s,known_x’s)来计算直线,或用函数GROWTH(known_y’s,known_x’s)来计算指数曲线。这些不带参数new_x’s的函数可在实际数据点上根据直线或曲线来返回y的数组值,然后可以将预测值与实际值进行比较。还可以用图表方式来直观地比较二者。
5)回归分析时,Excel计算每一点的y的估计值和实际值的平方差。这些平方差之和称为残差平方和(ssresid)。然后Excel计算总平方和(sstotal)。当const=TRUE或被删除时,总平方和是y的实际值和平均值的平方差之和。当const=FALSE时,总平方和是y的实际值的平方和(不需要从每个y值中减去平均值)。回归平方和(ssreg)可通过公式ssreg=sstotal-ssresid计算出来。残差平方和与总平方和的比值越小,判定系数r2的值就越大,r2是表示回归分析公式的结果反映变量间关系的程度的标志。r2=ssreg/sstotal。
6)在某些情况下,一个或多个X列可能没有出现在其他X列中的预测值(假设Y’s和X’s位于列中)。换句话说,删除一个或多个X列可能导致同样精度的y预测值。在这种情况下,这些多余的X列应该从回归模型中删除。这种现象被称为“共线”,因为任何多余的X列可表示为多个非多余X列的和。LINEST将检查是否存在共线,并在识别出来之后从回归模型中删除任何多余的X列。由于包含0系数以及0se’s,所以已删除的X列能在LINEST输出中被识别出来。如果一个或多个多余的列被删除,则将影响df,原因是df取决于被实际用于预测目的的X列的个数。如果由于删除多余的X列而更改了df,则也会影响sey和F的值。
实际上,出现共线的情况应该相对很少。但是,如果某些X列仅包含0’s和1’s作为一个实验中的对象是否属于某个组的指示器,则很可能引起共线。如果const=TRUE或被删除,则LINEST可有效地插入所有1’s的其他X列,以便模型化截取。如果在一列中,1对应于每个男性对象,0对应于非男性对象;而在另一列中,1对应于每个女性对象,0对应于非女性对象,那么后一列就是多余的,因为其中的项可通过从所有1’s(由LINEST添加)的另一列中减去“男性指示器”列中的项来获得。
7)df的计算方法如下所示(没有X列由于共线而从模型中被删除)。如果存在known_x’s的k列和const=TRUE或被删除,那么df=n–k–1。如果const=FALSE,那么df=n–k。在这两种情况下,每次由于共线而删除一个X列都会使df加1。
8)对于返回结果为数组的公式,必须以数组公式的形式输入。
当输入一个数组常量(如known_x’s)作为参数时,以逗号作为同一行中各数值的分隔符,以分号作为不同行中各数值的分隔符。分隔符可能因“控制面板”的“区域和语言选项”中区域设置的不同而有所不同。
9)如果y的回归分析预测值超出了用来计算公式的y值的范围,它们可能是无效的。
函数LINEST中使用的下层算法与函数SLOPE和INTERCEPT中使用的下层算法不同。当数据未定且共线时,这些算法之间的差异会导致不同的结果。例如,如果参数known_y’s的数据点为0,参数known_x’s的数据点为1:
LINEST返回值0。LINEST算法用来返回共线数据的合理结果,在这种情况下至少可找到一个答案。
SLOPE和INTERCEPT返回错误#DIV/0!。SLOPE和INTERCEPT算法用来查找一个且仅一个答案,在这种情况下可能有多个答案。
10)除了使用LOGEST计算其他回归分析类型的统计值外,还可以使用LINEST计算其他回归分析类型的范围,方法是将x和y变量的函数作为LINEST的x和y系列输入。例如,下面的公式:
=LINEST(yvalues,xvalues^COLUMN($A:$C))
将在使用y值的单个列和x值的单个列计算下面的方程式的近似立方(多项式次数3)值时运行:
y=m1*x+m2*x^2+m3*x^3+b
可以调整此公式以计算其他类型的回归,但是在某些情况下,需要调整输出值和其他统计值。