已知某函数的若干离散函数值{f1,f2,…,fn},通过调整该函数中若干待定系数f(λ1,λ2,…,λm),使得该函数与已知点集的差别(最小二乘意义)最小。如果待定函数是线性,就叫线性拟合或者线性回归(主要在统计中)。线性拟合作为数学计算中一种常用的数学方法,在建筑、物理、化学、甚至天体物理、航天中都得到基本的应用。一般情况下,线性拟合需要根据实际需要,取用不同的拟合度,即R2。线性拟合函数LINEST的功能是使用最小二乘法对已知数据进行最佳直线拟合,并返回描述此直线的数组。因为此函数返回数组数据,所以必须以数组公式的形式输入。该函数语法格式为:LINEST(known_y’s,known_x’s,const,stats)。Known_y’s是关系表达式y=mx+b中已知的y值集合;Known_x’s是关系表达式y=mx+b中已知的可选x值集合;const为一逻辑值,用于指定是否将常量b强制设为0,如果const为TRUE或省略,b将按正常计算,如果const为FALSE,b将被设为0,并同时调整m值使y=mx;stats为一逻辑值,指定是否返回附加回归统计值,为TRUE时返回附归统计值,为FALSE或省略,只返回系数m和常量b。
LINEST函数返回的附加回归统计值(根据数据的位置)说明如表16-1所示。
表16-1 LINEST函数回归统计值说明
接下来我们利用上面所述营业费用预测案例来介绍LINEST函数的具体使用方法。
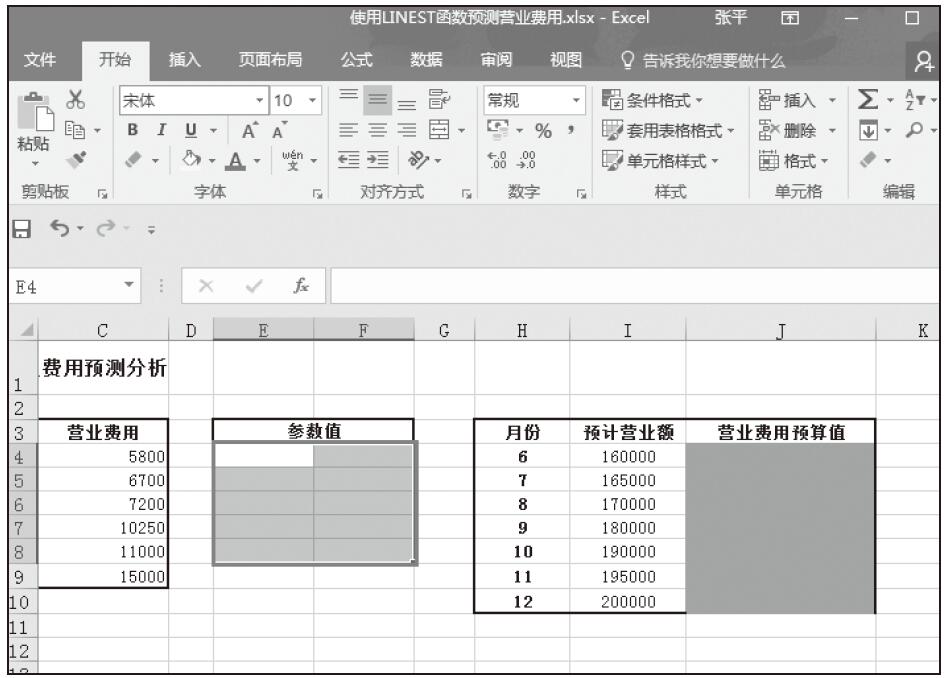
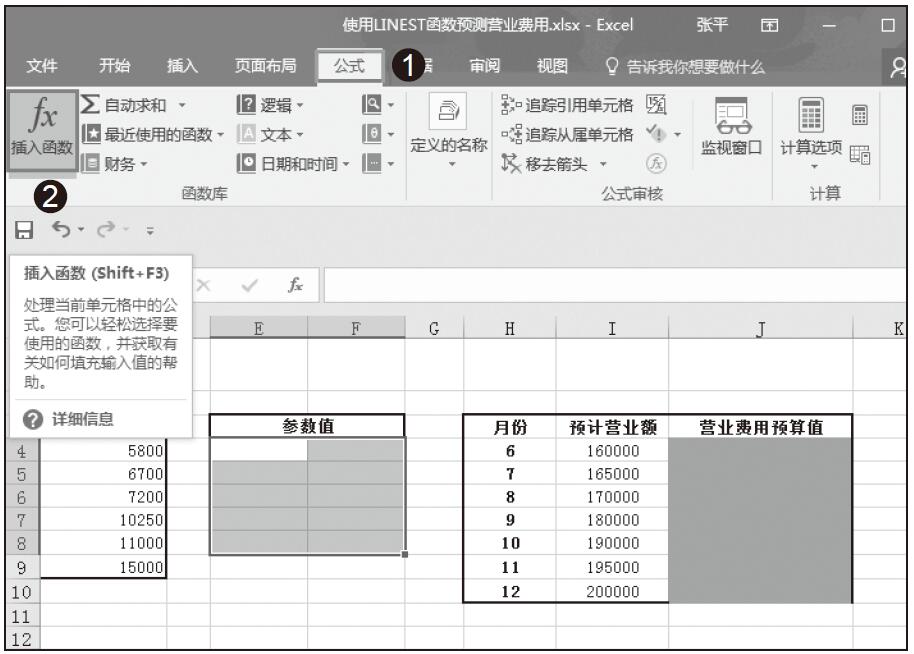
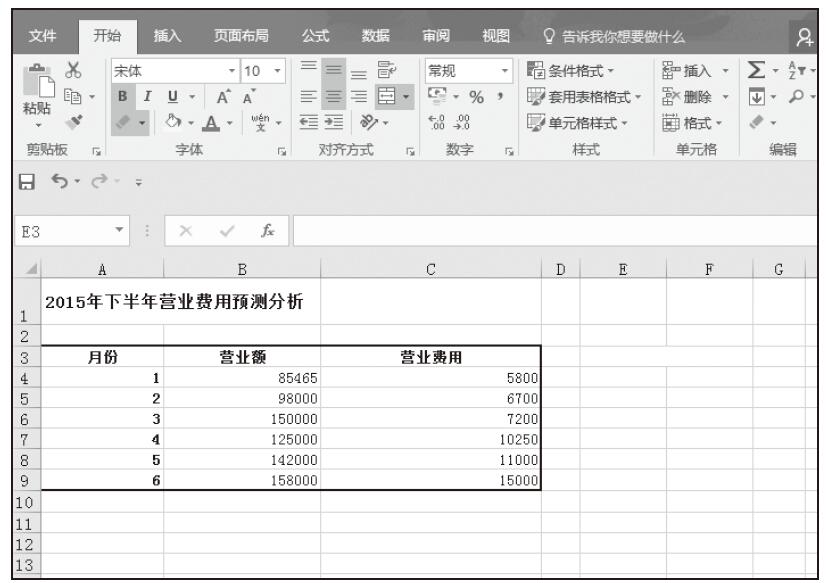
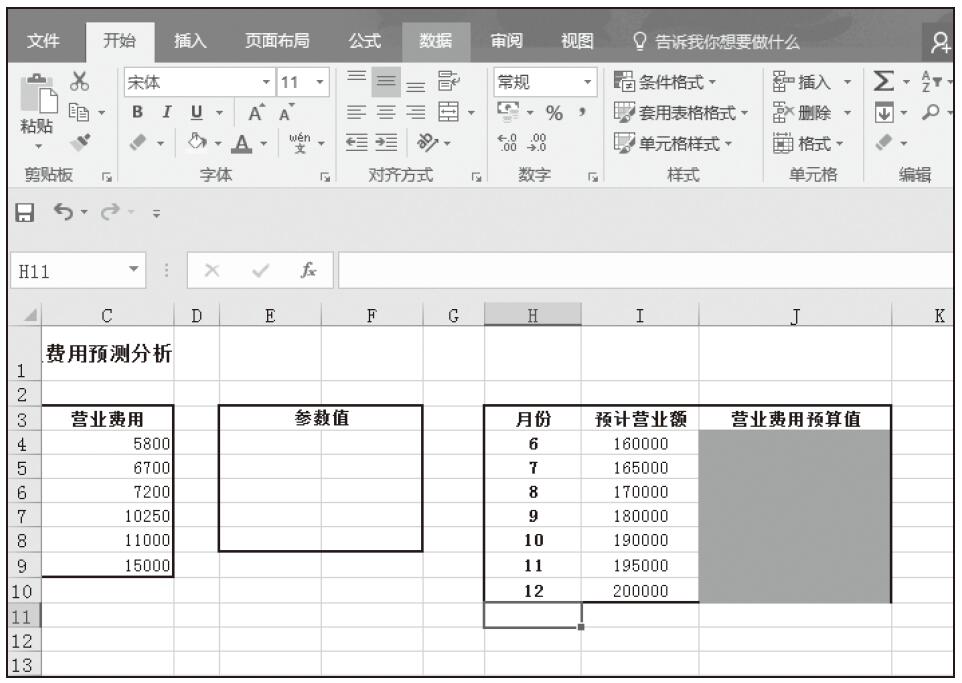
步骤01:选择单元格区域E4:F8,如图16-15所示。
图16-15 选择单元格区域
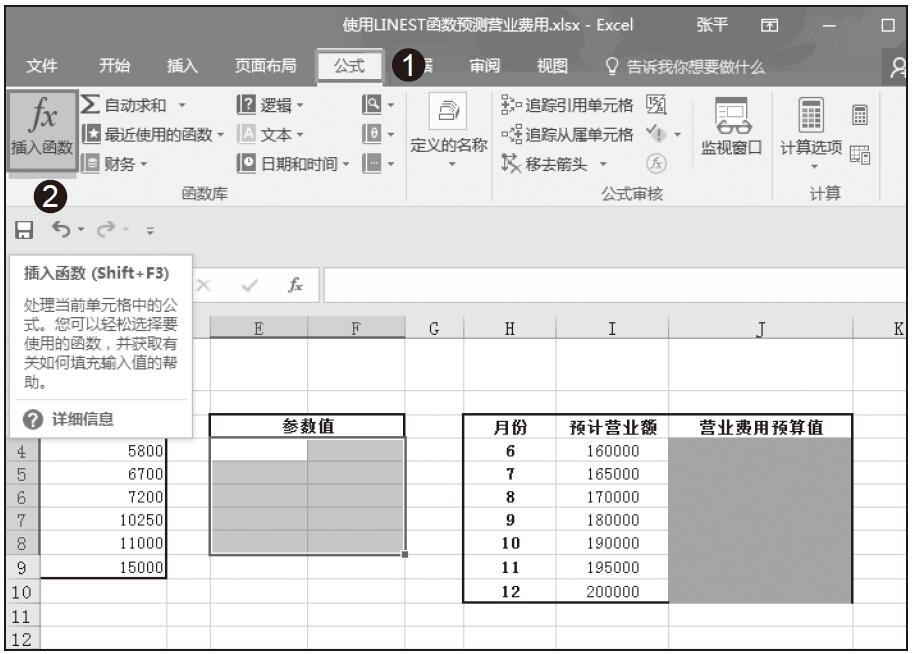
步骤02:在“公式”选项卡中的“函数库”组中单击“插入函数”按钮,如图16-16所示。
图16-16 单击“插入函数”按钮
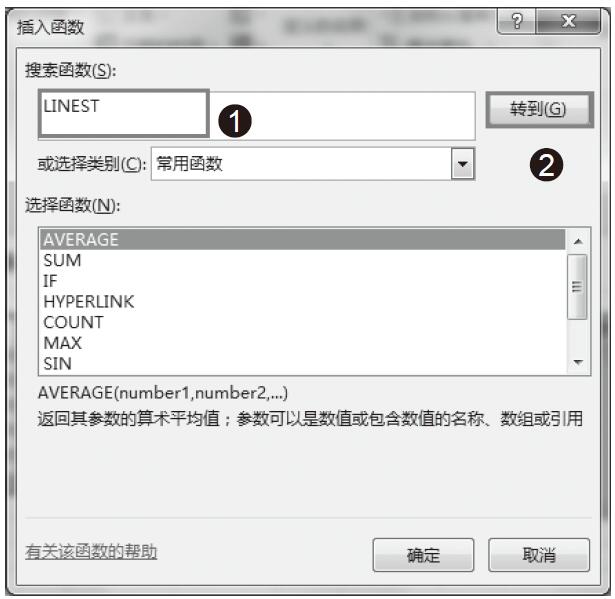
步骤03:在“插入函数”对话框中的“搜索函数”框中输入函数名称LINEST,然后单击“转到”按钮,如图16-17所示。
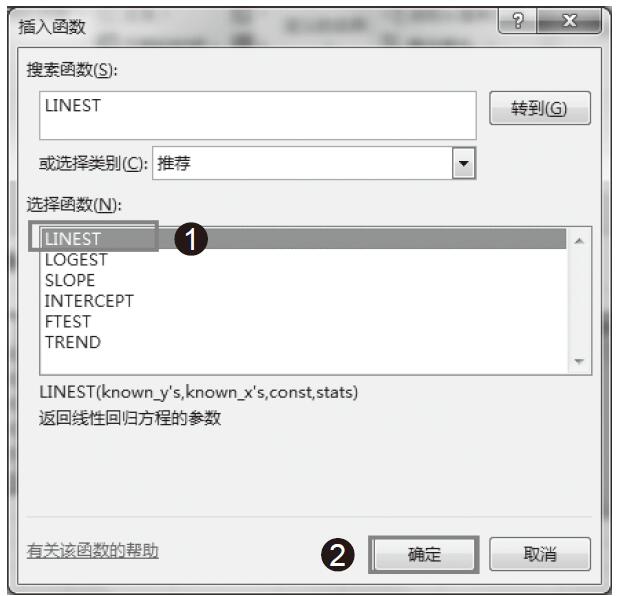
步骤04:此时在“选择函数”列表框中会显示与搜索函数相关的一系列函数,选择需要的函数LINEST,然后单击“确定”按钮,如图16-18所示。
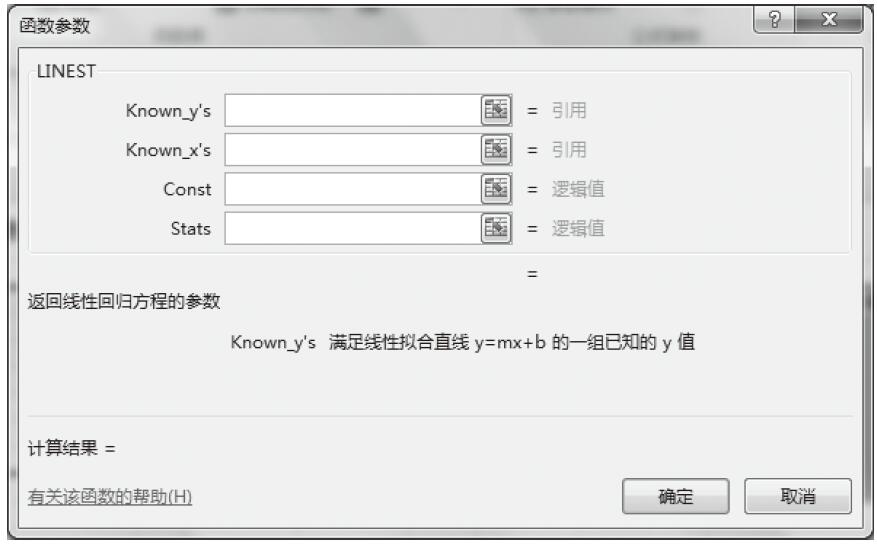
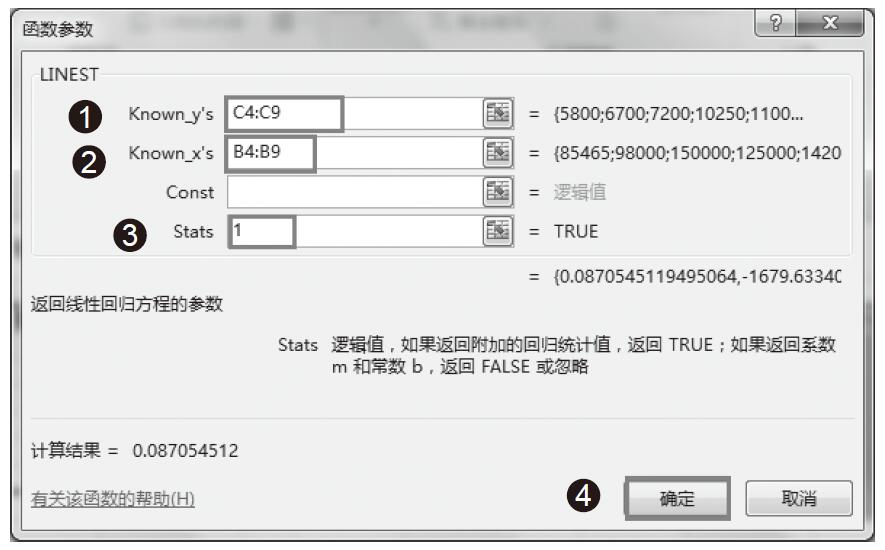
步骤05:随后屏幕上弹出“函数参数”对话框,如图16-19所示。
步骤06:设置known_y’s参数为单元格区域C4:C9,设置known_x’s参数为单元格区域B4:B9,const参数省略,为空,stats参数设置为1,然后单击“确定”按钮,如图16-20所示。
图16-17 搜索函数
图16-18 选择函数
图16-19 弹出“函数参数”对话框
图16-20 设置函数参数
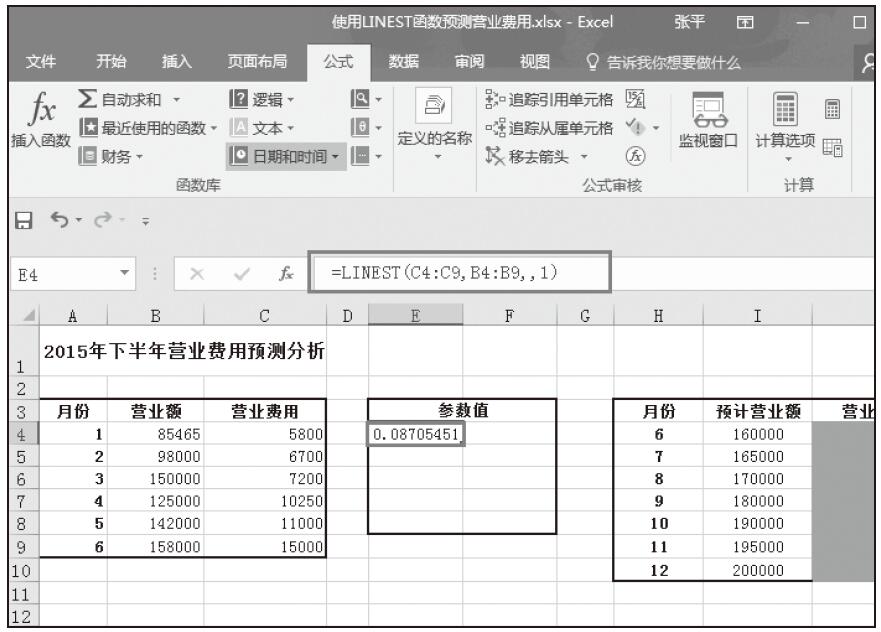
步骤07:此时函数计算结果如图16-21所示。只返回了一个值,并没有返回回归附加值,这是因为此时函数并没有作为数组公式输入。
图16-21 函数计算结果
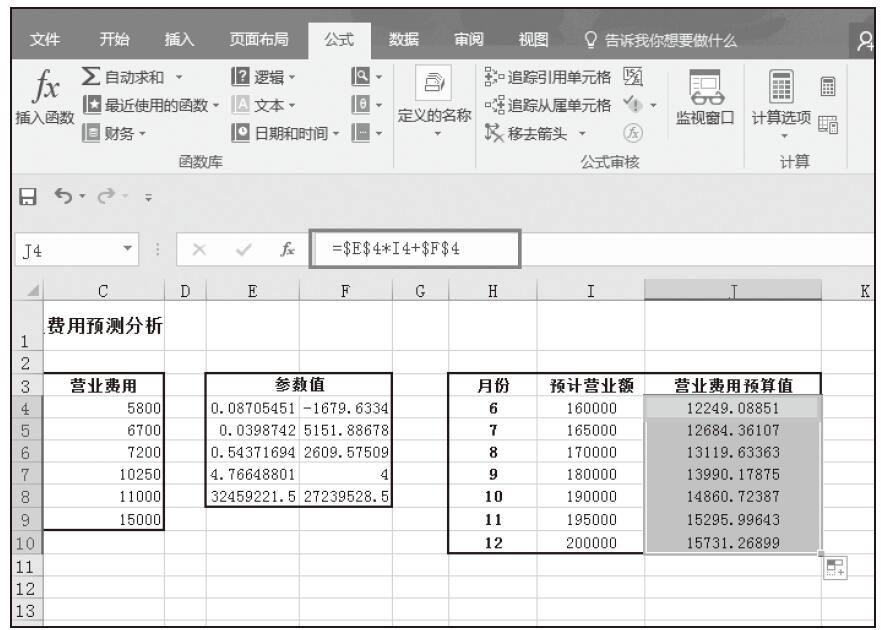
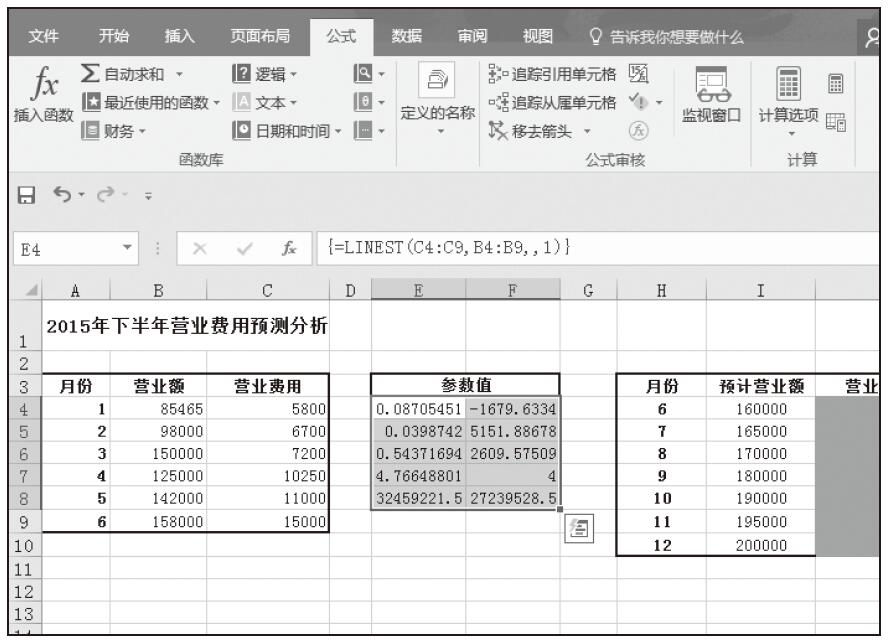
步骤08:在编辑栏中单击,使公式处于编辑状态,然后按下键盘上的组合键Ctrl+Shift+Enter,数组公式返回结果如图16-22所示,单元格E4和F4中的值分别对应参数m和b。
图16-22 更改为数组公式