标签：利息与利率计算函数

Excel 应用RATE函数计算年金的各期利率

RATE函数用于计算年金的各期利率。函数RATE通过迭代法计算得出，并且可能无解或有多个解。如果在进行20次迭代计算后，函数RATE的相邻两次结果没有收敛于0.0000001，函数RATE将返回错误值“#NUM！”。RATE函数的语法如下。

RATE(nper,pmt,pv,fv,type,guess)

有关参数nper、pmt、pv、fv及type的详细说明，可以参阅函数PV。参数nper为总投资期，即该项投资的付款期总数。pmt为各期所应支付的金额，其数值在整个年金期间保持不变。通常，pmt包括本金和利息，但不包括其他费用或税款。如果忽略pmt，则必须包含fv参数。pv为现值，即从该项投资开始计算时已经入账的款项，或一系列未来付款当前值的累积和，也称为本金。

fv为未来值，或在最后一次付款后希望得到的现金余额。如果省略fv，则假设其值为零。type为数字0或1，用以指定各期的付款时间是在期初还是期末。guess为预期利率。如果省略预期利率，则假设该值为10%。如果函数RATE不收敛，则需要改变guess的值。通常当guess位于0到1之间时，函数RATE是收敛的。

典型案例

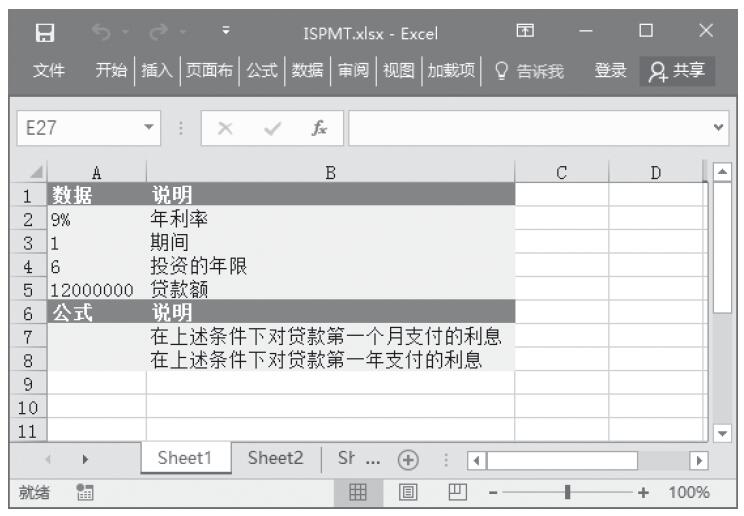
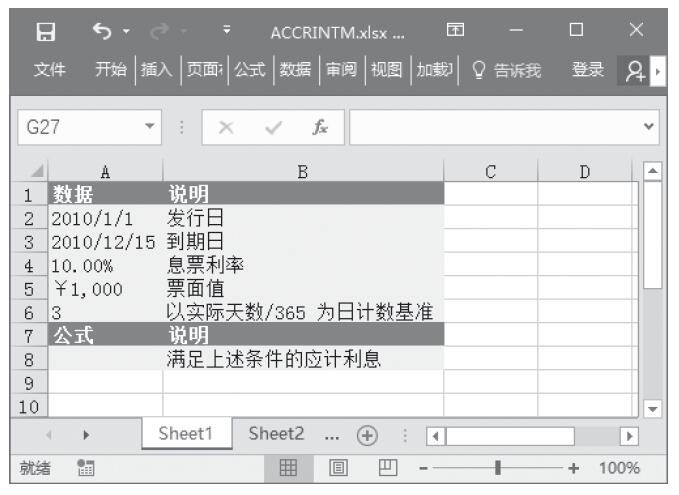
已知贷款期限、每月支付额和贷款额，计算这些条件下的贷款月利率和年利率。基础数据如图17-19所示。

步骤1：打开例子工作簿“RATE.xlsx”。

步骤2：在单元格A6中输入公式“=RATE（A2*12，A3，A4）”，用于计算在上述条件下贷款的月利率。

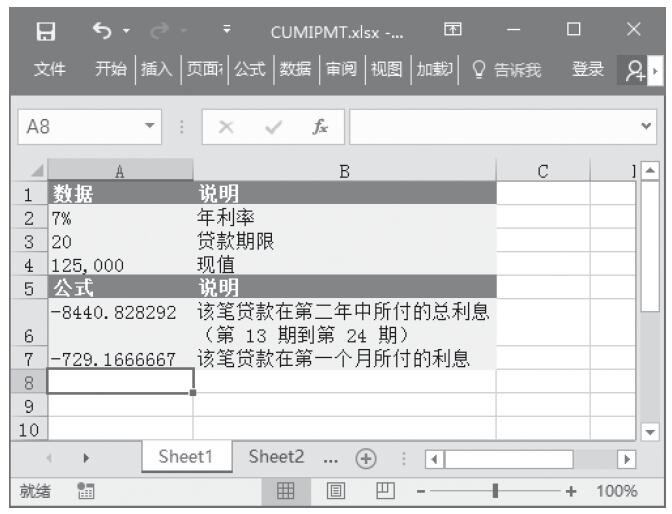
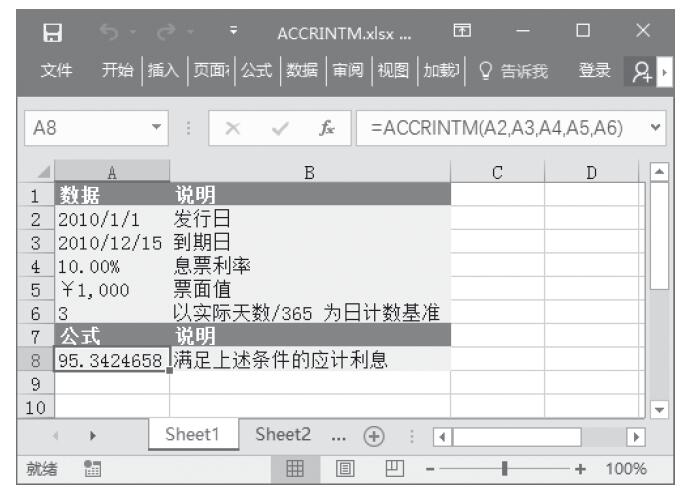
步骤3：在单元格A7中输入公式“=RATE（A2*12，A3，A4）*12”，用于计算在上述条件下贷款的年利率。计算结果如图17-20所示。

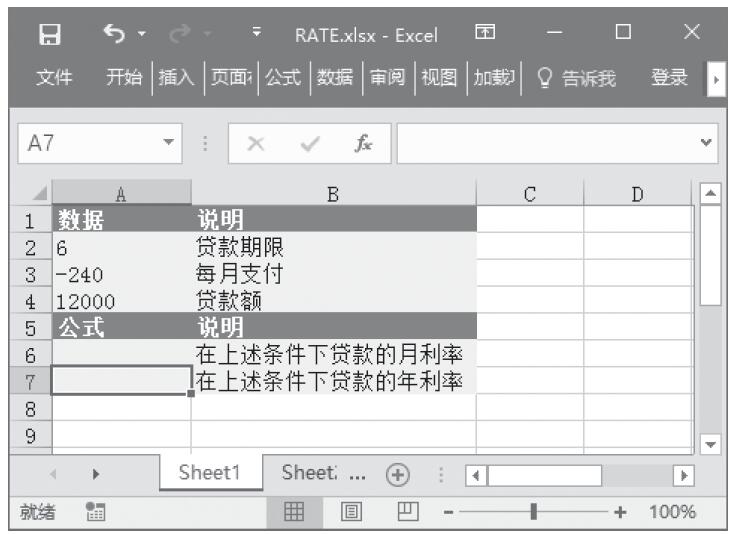
图17-19　基础数据

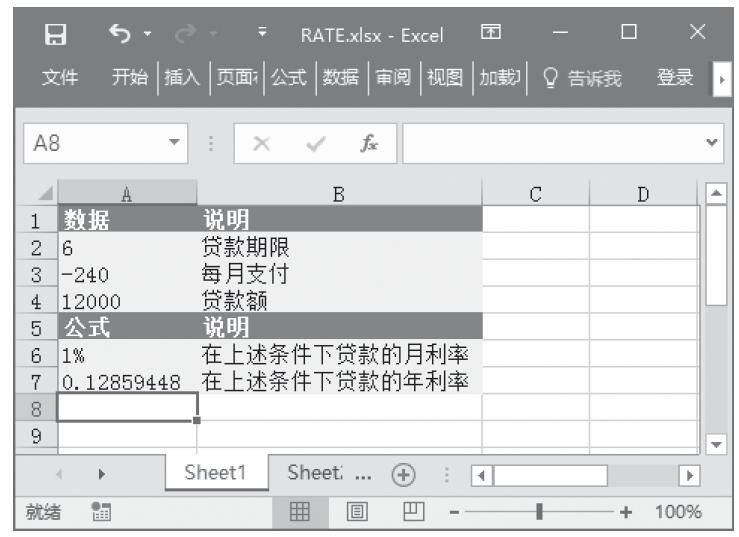
图17-20　计算结果

使用指南

应确认所指定的guess和nper单位的一致性，对于年利率为12%的四年期贷款，如果按月支付，guess为12%/12，nper为4*12；如果按年支付，guess为12%，nper为4。

Excel 应用NOMINAL函数计算年度的名义利率

NOMINAL函数用于基于给定的实际利率和年复利期数，计算名义年利率。NOMINAL函数的语法如下。

NOMINAL(effect_rate,npery)

其中参数effect_rate为实际利率，npery为每年的复利期数。

典型案例

已知某债券的实际利率、每年的复利期数，计算这些条件下的名义利率。基础数据如图17-17所示。

步骤1：打开例子工作簿“NOMINAL.xlsx”。

步骤2：在单元格A5中输入公式“=NOMINAL（A2，A3）”，用于计算名义利率。计算结果如图17-18所示。

图17-17　基础数据

图17-18　计算结果

使用指南

npery若非整数将被截尾取整。如果任一参数为非数值型，函数NOMINAL返回错误值“#VALUE！”；如果effect_rate≤0或npery<1，函数NOMINAL返回错误值“#NUM！”。函数NOMINAL与函数EFFECT相关，如下式所示：

Excel 应用ISPMT函数计算特定投资期内要支付的利息

ISPMT函数用于计算特定投资期内要支付的利息。Excel提供此函数是为了与Lotus1-2-3兼容。ISPMT函数的语法如下。

ISPMT(rate,per,nper,pv)

其中参数rate为投资的利率。per为要计算利息的期数，此值必须在1到nper之间。nper为投资的总支付期数。pv为投资的当前值。对于贷款，pv为贷款数额。

典型案例

已知某贷款的年利率、利息的期数、投资的年限、贷款额，计算在这些条件下对贷款第一个月支付的利息和对贷款第一年支付的利息。基础数据如图17-15所示。

步骤1：打开例子工作簿“ISPMT.xlsx”。

步骤2：在单元格A7中输入公式“=ISPMT（A2/12，A3，A4*12，A5）”，用于计算对贷款第一个月支付的利息。

步骤3：在单元格A8中输入公式“=ISPMT（A2，1，A4，A5）”，用于计算对贷款第一年支付的利息。计算结果如图17-16所示。

图17-15　基础数据

图17-16　计算结果

使用指南

应确认所指定的rate和nper单位的一致性。例如，同样是四年期年利率为12%的贷款，如果按月支付，rate应为12%/12，nper应为4*12；如果按年支付，rate应为12%，nper为4。对所有参数，都以负数代表现金支出（如存款或他人取款），以正数代表现金收入（如股息分红或他人存款）。

Excel 应用IPMT函数计算一笔投资在给定期数内的利息偿还额

IPMT函数用于基于固定利率及等额分期付款方式，计算给定期数内对投资的利息偿还额。IPMT函数的语法如下。

IPMT(rate,per,nper,pv,fv,type)

其中参数rate为各期利率。per用于计算其利息数额的期数，必须在1到nper之间。nper为总投资期，即该项投资的付款期总数。pv为现值，或一系列未来付款的当前值的累积和。fv为未来值，或在最后一次付款后希望得到的现金余额。如果省略fv，则假设其值为零（例如，一笔贷款的未来值即为零）。type数字0或1，用以指定各期的付款时间是在期初还是期末。如果省略type，则假设其值为零。

典型案例

已知某贷款的年利率、用于计算其利息数额的期数、贷款的年限、贷款的现值，计算在这些条件下贷款第一个月的利息和贷款最后一年的利息。基础数据如图17-13所示。

步骤1：打开例子工作簿“IPMT.xlsx”。

步骤2：在单元格A7中输入公式“=IPMT（A2/12，A3*3，A4，A5）”，用于计算贷款第一个月的利息。

步骤3：在单元格A8中输入公式“=IPMT（A2，3，A4，A5）”，用于计算贷款最后一年的利息（按年支付）。计算结果如图17-14所示。

图17-13　基础数据

图17-14　计算结果

使用指南

应确认所指定的rate和nper单位的一致性。例如，同样是四年期年利率为12%的贷款，如果按月支付，rate应为12%/12，nper应为4*12；如果按年支付，rate应为12%，nper为4。对于所有参数，支出的款项，如银行存款，表示为负数；收入的款项，如股息收入，表示为正数。

Excel 应用INTRATE函数计算完全投资型证券的利率

INTRATE函数用于计算一次性付息证券的利率。INTRATE函数的语法如下：

INTRATE(settlement,maturity,investment,redemption,basis)

其中参数settlement为证券的结算日，结算日是在发行日之后，证券卖给购买者的日期。maturity为有价证券的到期日，到期日是有价证券有效期截止时的日期。investment为有价证券的投资额。redemption为有价证券到期时的清偿价值。basis为日计数基准类型。

典型案例

已知某债券的结算日、到期日、投资额、清偿价值等信息，计算在此债券期限的贴现率。基础数据如图17-11所示。

步骤1：打开例子工作簿“INTRATE.xlsx”。

步骤2：在单元格A8中输入公式“=INTRATE（A2，A3，A4，A5，A6）”，用于计算在此债券期限的贴现率。计算结果如图17-12所示。

图17-11　基础数据

图17-12　计算结果

使用指南

参数settlement、maturity和basis若非整数将被截尾取整。如果settlement或maturity不是合法日期，函数INTRATE返回错误值“#VALUE！”；如果investment≤0或redemption≤0，函数INTRATE返回错误值“#NUM！”；如果basis<0或basis>4，函数INTRATE返回错误值“#NUM！”；如果settlement≥maturity，函数INTRATE返回错误值“#NUM！”。函数INTRATE的计算公式如下。

式中：

B为一年之中的天数，取决于年基准数。

DIM为结算日与到期日之间的天数。

Excel 应用EFFECT函数计算年有效利率

EFFECT函数利用给定的名义利率和每年的复利期数，计算有效的年利率。EFFECT函数的语法如下。

EFFECT(nominal_rate,npery)

其中参数nominal_rate为名义利率，npery为每年的复利期数。

典型案例

已知某贷款的名义利率与每年的复利期数，计算满足这些条件的有效利率。基础数据如图17-9所示。

步骤1：打开例子工作簿“EFFECT.xlsx”。

步骤2：在单元格A5中输入公式“=EFFECT（A2，A3）”，用于计算。计算结果如图17-10所示。

图17-9　基础数据

图17-10　计算结果

使用指南

npery若非整数将被截尾取整。如果任一参数为非数值型，函数EFFECT返回错误值“#VALUE！”；如果nominal_rate≤0或npery<1，函数EFFECT返回错误值“#NUM！”。函数EFFECT的计算公式为：

Excel 应用CUMIPMT函数计算两个付款期之间累积支付的利息

CUMIPMT函数用于计算一笔贷款在给定的start_period到end_period期间累计偿还的利息数额。CUMIPMT函数的语法如下。

CUMIPMT(rate,nper,pv,start_period,end_period,type)

其中参数rate为利率，nper为总付款期数，pv为现值。start_period为计算中的首期，付款期数从1开始计数。end_period为计算中的末期。type为付款时间类型，为0时付款类型为期末付款，为1时付款类型为期初付款。

典型案例

已知某笔贷款的年利率、贷款期限、现值，计算该笔贷款在第一个月所付的利息。基础数据如图17-7所示。

步骤1：打开例子工作簿“CUMIPMT.xlsx”。

步骤2：在单元格A6中输入公式“=CUMIPMT（A2/12，A3*12，A4，13，24，0）”，用于计算该笔贷款在第2年中所付的总利息（第13期到第24期）。

步骤3：在单元格A7中输入公式“=CUMIPMT（A2/12，A3*12，A4，1，1，0）”，用于计算该笔贷款在第一个月所付的利息。计算结果如图17-8所示。

图17-7　基础数据

图17-8　计算结果

使用指南

应确认所指定的rate和nper单位的一致性。例如，同样是四年期年利率为10%的贷款，如果按月支付，rate应为10%/12，nper应为4*12；如果按年支付，rate应为10%，nper为4。nper、start_period、end_period和type若非整数将被截尾取整。如果rate≤0、nper≤0或pv≤0，函数CUMIPMT返回错误值“#NUM！”；如果start_period<1、end_period<1或start_period>end_period，函数CUMIPMT返回错误值“#NUM！”；如果type不是数字0或1，函数CUMIPMT返回错误值“#NUM！”。

Excel 应用COUPNUM函数计算结算日和到期日之间的应付利息次数

COUPNUM函数的语法如下：

COUPNUM(settlement,maturity,frequency,basis)

其中参数settlement为证券的结算日。结算日是在发行日之后，证券卖给购买者的日期。maturity为有价证券的到期日。到期日是有价证券有效期截止时的日期。frequency为年付息次数。如果按年支付，frequency=1；按半年期支付，frequency=2；按季支付，frequency=4。basis为日计数基准类型。

典型案例

已知某债券的结算日、到期日等信息，计算满足这些条件的债券的付息次数。基础数据如图17-5所示。

步骤1：打开例子工作簿“COUPNUM.xlsx”。

步骤2：在单元格A7中输入公式“=COUPNUM（A2，A3，A4，A5）”，用于计算债券的付息次数。计算结果如图17-6所示。

图17-5　基础数据

图17-6　计算结果

使用指南

“结算日”是购买者买入息票（如债券）的日期。“到期日”是息票有效期截止时的日期。例如，在2008年1月1日发行的30年期债券，六个月后被购买者买走，则发行日为2008年1月1日，结算日为2008年7月1日，而到期日是在发行日2008年1月1日的30年后，即2038年1月1日。所有参数若非整数将被截尾取整。如果settlement或maturity不是合法日期，则COUPNUM将返回错误值“#VALUE！”；如果frequency不为1、2或4，则COUPNUM将返回错误值“#NUM！”；如果basis<0或者basis>4，则COUPNUM返回错误值“#NUM！”；如果settlement≥maturity，则COUPNUM返回错误值“#NUM！”。

Excel 应用ACCRINTM函数计算在到期日支付利息的证券的应计利息

ACCRINTM函数用于计算到期一次性付息有价证券的应计利息。ACCRINTM函数的语法如下。

ACCRINTM(issue,settlement,rate,par,basis)

其中参数issue为有价证券的发行日，settlement为有价证券的到期日，rate为有价证券的年息票利率。par为有价证券的票面价值，如果省略par，函数ACCRINTM视par为￥1000。basis为日计数基准类型。表17-1为参数basis的日计数基准。

典型案例

已知某债券的发行日、到期日、息票利率、票面值等信息，计算满足这些条件的应计利息。基础数据如图17-3所示。

步骤1：打开例子工作簿“ACCRINTM.xlsx”。

步骤2：在单元格A8中输入公式“=ACCRINTM（A2，A3，A4，A5，A6）”，计算结果如图17-4所示。

图17-3　基础数据

图17-4　计算结果

使用指南

参数Issue、settlement和basis若非整数将被截尾取整。如果issue或settlement不是有效日期，函数ACCRINTM返回错误值“#VALUE！”；如果利率为0或票面价值为0，函数ACCRINTM返回错误值“#NUM！”；如果basis<0或basis>4，函数ACCRINTM返回错误值“#NUM！”；如果issue≥settlement，函数ACCRINTM返回错误值“#NUM！”；ACCRINTM的计算公式如下。

式中：

A=按月计算的应计天数。在计算到期付息的利息时指发行日与到期日之间的天数。

D=年基准数。

Excel 应用ACCRINT函数计算定期支付利息的证券的应计利息

ACCRINT函数用于计算定期付息证券的应计利息。ACCRINT函数的语法如下。

ACCRINT(issue,first_interest,settlement,rate,par,frequency,basis,calc_method)

其中参数issue表示有价证券的发行日，first_interest表示证券的首次计息日，settlement表示证券的结算日。结算日是指在发行日之后，证券卖给购买者的日期。rate表示有价证券的年息票利率。par表示证券的票面值，如果该参数被省略，则ACCRINT函数将使用￥1000。frequency表示年付息次数。如果按年支付，参数frequency=1；按半年期支付，参数frequency=2；按季支付，参数frequency=4。basis表示日计数基准类型。表17-1为参数basis的日计数基准。

表17-1　参数basis的日计数基准

参数calc_method表示逻辑值，指定当结算日期晚于首次计息日期时，用于计算总应计利息的方法。如果值为TRUE（1），则计算从发行日到结算日的总应计利息；如果值为FALSE（0），则计算从首次计息日到结算日的应计利息；如果此参数被省略，则默认值为TRUE。

典型案例

已知国债的发行日、首次计息日、结算日、票息率、票面值等信息，计算定期支付利息的债券的应计利息。基础数据如图17-1所示。

步骤1：打开例子工作簿“ACCRINT.xlsx”。

步骤2：在单元格A10中输入公式“=ACCRINT（A2，A3，A4，A5，A6，A7，A8）”，用于计算满足上述条件的国债应计利息。

步骤3：在单元格A11中输入公式“=ACCRINT（DATE（2016，3，5），A3，A4，A5，A6，A7，A8）”，用于计算满足上述条件（除发行日为2016年3月5日之外）的应计利息。

步骤4：在单元格A12中输入公式“=ACCRINT（DATE（2016，4，5），A3，A4，A5，A6，A7，A8，TRUE）”，用于计算满足上述条件（除发行日为2016年4月5日且应计利息从首次计息日计算到结算日之外）的应计利息。计算结果如图17-2所示。

图17-1　基础数据

图17-2　计算结果

使用指南

参数issue、first_interest、settlement、frequency和basis若非整数将被截尾取整。如果参数issue、first_interest或settlement不是有效日期，则ACCRINT函数将返回错误值“#VALUE！”；如果参数rate≤0或参数par≤0，则ACCRINT函数将返回错误值“#NUM！”；如果参数frequency不是数字1、2或4，则ACCRINT将返回错误值“#NUM！”；如果参数basis<0或basis>4，则ACCRINT将返回错误值“#NUM！”；如果参数issue≥settlement，则ACCRINT函数将返回错误“#NUM！”。

函数ACCRINT的计算公式如下。

其中：

Ai=奇数期内第i个准票息期的应计天数。

NC=奇数期内的准票息期期数。如果该数含有小数位，则向上进位至最接近的整数。

NLi=奇数期内第i个准票息期的正常天数。