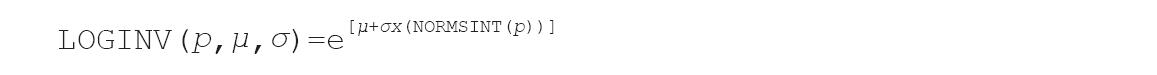LOGNORMDIST函数用于计算返回x的对数累积分布函数，其中ln（x）是服从参数mean和standard_dev的正态分布。使用此函数可以分析经过对数变换的数据。LOGNORMDIST函数的语法如下。
LOGNORMDIST(x,mean,standard_dev)
其中参数x为参数值。mean为ln（x）的平均值。standard_dev为ln（x）的标准偏差。
已知参数值x、ln（x）的平均值、ln（x）的标准偏差，计算在此条件下0.482859的对数正态累积分布函数值。基础数据如图16-65所示。
步骤1：打开例子工作簿“LOGNORMDIST.xlsx”。
步骤2：在单元格A6中输入公式“=LOGNORMDIST（A2，A3，A4）”，用于计算总体平均值的置信区间。计算结果如图16-66所示。
图16-65 基础数据
图16-66 计算结果
如果任一参数为非数值型，函数LOGNORMDIST返回错误值“#VALUE！”。如果x≤0或standard_dev≤0，函数LOGNORMDIST返回错误值“#NUM！”。对数累积分布函数的计算公式如下：
LOGINV函数用于计算x的对数累积分布函数的反函数，此处的ln（x）是含有mean与standard_dev参数的正态分布。如果p=LOGNORMDIST（x，…），则LOGINV（p，…）=x。使用对数分布可分析经过对数变换的数据。LOGINV函数的语法如下。
LOGINV(probability,mean,standard_dev)
其中参数probability是与对数分布相关的概率，mean为ln（x）的平均值，standard_dev为ln（x）的标准偏差。
已知与对数分布相关的概率、ln（x）的平均值、ln（x）的标准偏差，计算对数正态累积分布函数的反函数值。基础数据如图16-63所示。
步骤1：打开例子工作簿“LOGINV.xlsx”。
步骤2：在单元格A6中输入公式“=LOGINV（A2，A3，A4）”，用于计算对数正态累积分布函数的反函数值。计算结果如图16-64所示。
图16-63 基础数据
图16-64 计算结果
如果变量为非数值参数，则函数LOGINV返回错误值“#VALUE！”。如果probability＜0或probability＞1，则函数LOGINV返回错误值“#NUM！”。如果standard_dev≤0，则函数LOGINV返回错误值“#NUM！”。对数分布函数的反函数为：
GROWTH函数用于根据现有的数据预测指数增长值。根据现有的x值和y值，GROWTH函数返回一组新的x值对应的y值。可以使用GROWTH工作表函数来拟合满足现有x值和y值的指数曲线。GROWTH函数的语法如下。
GROWTH(known_y's,known_x's,new_x's,const)
其中参数known_y’s满足指数回归拟合曲线y=b×mx的一组已知的y值。known_x’s满足指数回归拟合曲线y=b×mx的一组已知的x值，为可选参数。new_x’s为需要通过GROWTH函数返回的对应y值的一组新x值。const为一逻辑值，用于指定是否将常数b强制设为1。
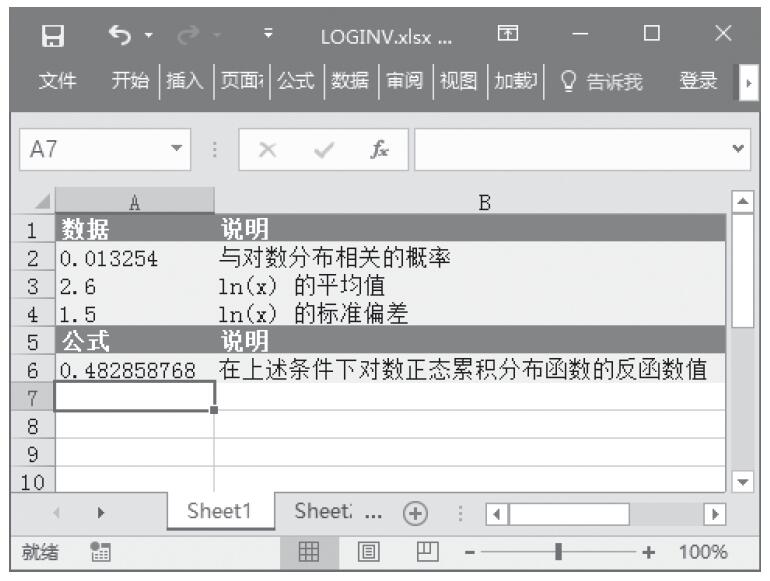
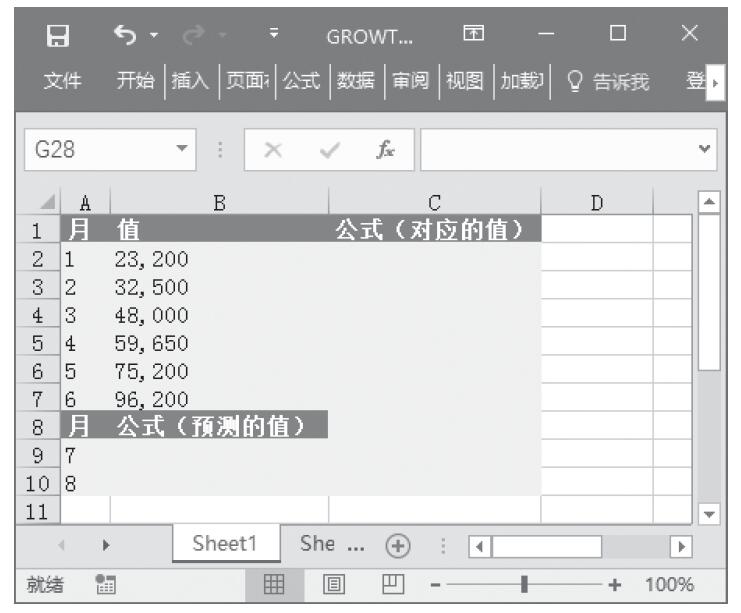
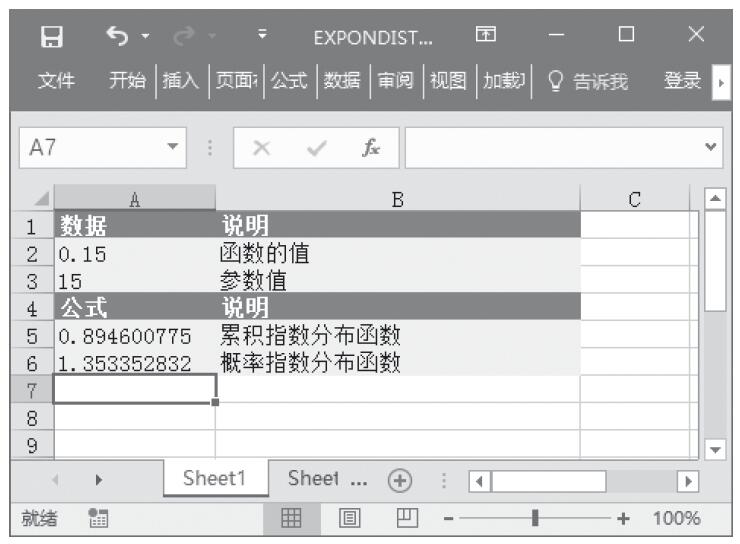
已知一组数据，根据现有数据预测指数增长值。基础数据如图16-61所示。
步骤1：打开例子工作簿“GROWTH.xlsx”。
步骤2：选中“C2：C7”单元格，按F2键，输入公式“=GROWTH（B2：B7，A2：A7）”，然后按“Ctrl+Shift+Enter”组合键以数组公式输入。
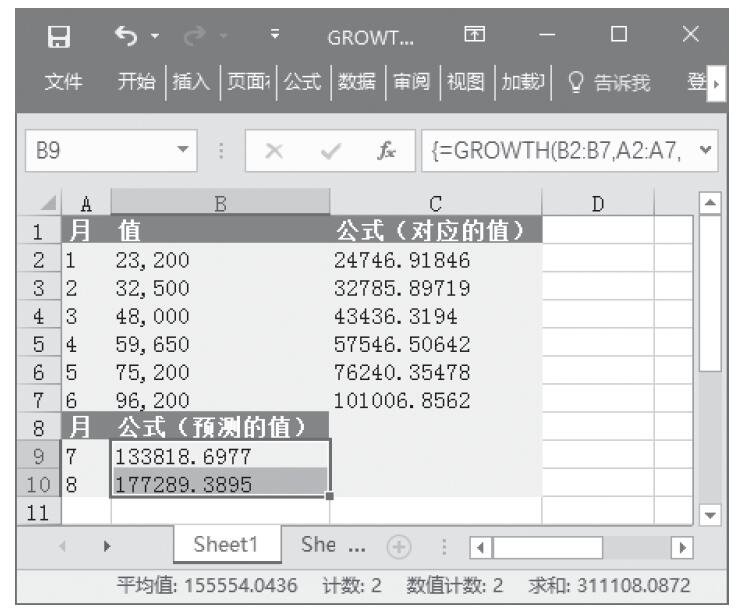
步骤3：选中“A9：A10”单元格，按F2键，输入公式“=GROWTH（B2：B7，A2：A7，A9：A10）”，然后按“Ctrl+Shift+Enter”组合键以数组公式输入。计算结果如图16-62所示。
图16-61 基础数据
图16-62 计算结果
1）如果数组known_y’s在单独一列中，则known_x’s的每一列被视为一个独立的变量。
2）如果数组known_y’s在单独一行中，则known_x’s的每一行被视为一个独立的变量。
3）如果known_y’s中的任何数为零或为负数，GROWTH函数将返回错误值“#NUM！”。
4）数组known_x’s可以包含一组或多组变量。如果仅使用一个变量，那么只要known_x’s和known_y’s具有相同的维数，则它们可以是任何形状的区域。如果用到多个变量，则known_y’s必须为向量（即必须为一行或一列）。
5）如果省略known_x’s，则假设该数组为{1，2，3，…}，其大小与known_y’s相同。
6）new_x’s与known_x’s一样，对每个自变量必须包括单独的一列（或一行）。因此，如果known_y’s是单列的，known_x’s和new_x’s应该有同样的列数。如果known_y’s是单行的，known_x’s和new_x’s应该有同样的行数。
7）如果省略new_x’s，则假设它和known_x’s相同。
8）如果known_x’s与new_x’s都被省略，则假设它们为数组{1，2，3，…}，其大小与known_y’s相同。
9）如果const为TRUE或省略，b将按正常计算。
10）如果const为FALSE，b将设为1，m值将被调整以满足y=m^x。
11）对于返回结果为数组的公式，在选定正确的单元格个数后，必须以数组公式的形式输入。
12）当为参数（如known_x’s）输入数组常量时，应当使用逗号分隔同一行中的数据，用分号分隔不同行中的数据。
GAMMALN函数用于计算一个值，可以使用该值构建总体平均值的置信区间。GAMMALN函数的语法如下。
GAMMALN(x)
其中参数x为需要计算函数GAMMALN的数值。
计算7的γ函数的自然对数。基础数据如图16-59所示。
步骤1：打开例子工作簿“GAMMALN.xlsx”。
步骤2：在单元格A2中输入公式“=GAMMALN（7）”，用于计算7的γ函数的自然对数。计算结果如图16-60所示。
图16-59 基础数据
图16-60 计算结果
如果x为非数值型，函数GAMMALN返回错误值“#VALUE！”。如果x≤0，函数GAMMALN返回错误值“#NUM！”。e的GAMMALN（i）次幂等于（i-1）！，其中i为整数。函数GAMMALN的计算公式如下：
GAMMALN=LN（Г（X））
式中：
EXPONDIST函数用于返回指数分布。使用函数EXPONDIST可以建立事件之间的时间间隔模型，例如，在计算银行自动提款机支付一次现金所花费的时间时，可通过函数EXPONDIST来确定这一过程最长持续一分钟的发生概率。EXPONDIST函数的语法如下。
EXPONDIST(x,lambda,cumulative)
其中参数x为函数的值。lambda为参数值。cumulative为一逻辑值，指定指数函数的形式。如果cumulative为TRUE，函数EXPONDIST返回累积分布函数；如果cumulative为FALSE，返回概率密度函数。
已知函数的值与参数值，试返回累积指数分布函数和概率指数分布函数。基础数据如图16-57所示。
图16-57 基础数据
步骤1：打开例子工作簿“EXPONDIST.xlsx”。
步骤2：在单元格A5中输入公式“=EXPONDIST（A2，A3，TRUE）”，用于返回累积指数分布函数。
步骤3：在单元格A6中输入公式“=EXPONDIST（0.2，10，FALSE）”，用于返回概率指数分布函数。计算结果如图16-58所示。
图16-58 计算结果
如果x或lambda为非数值型，函数EXPONDIST返回错误值“#VALUE！”。如果x＜0，函数EXPONDIST返回错误值“#NUM！”。如果lambda≤0，函数EXPONDIST返回错误值“#NUM！”。概率密度函数的计算公式为：
累积分布函数的计算公式为：
