GCD函数的功能是返回两个或多个整数的最大公约数,最大公约数是能分别将参数number1和number2除尽的最大整数。LCM函数的功能是,返回整数的最小公倍数。最小公倍数是所有整数参数number1、number2等的最小正整数倍数。两函数的语法分别如下:
GCD(number1,number2,…) LCM(number1,number2, …)
其中参数number1,number2,…为1到255个参数。如果参数不是整数,则截尾取整。
【典型案例】给出两个参数数值,求解两参数的最大公约数和最小公倍数。本例的原始数据如图13-24所示。
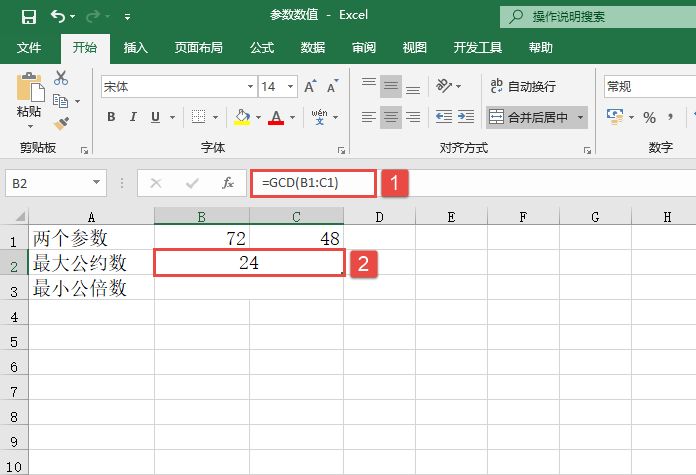
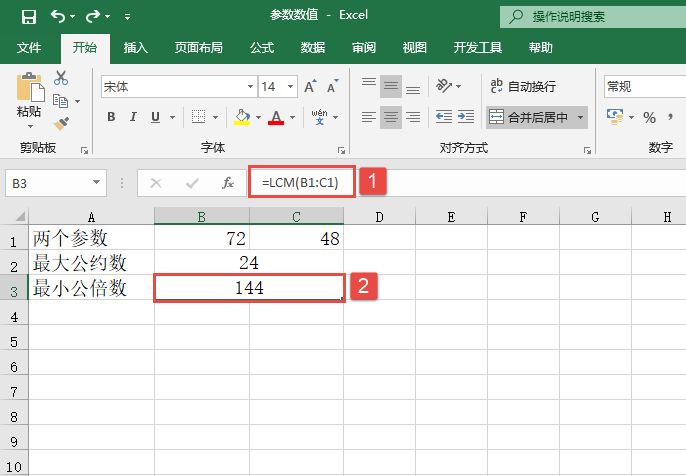
在B2单元格中输入公式“=GCD(B1:C1)”,计算两参数的最大公约数,结果为“24”。在B3单元格中输入公式“=LCM(B1:C1)”,计算两参数的最小公倍数,结果为“144”。如图13-25所示。
图13-24 原始数据
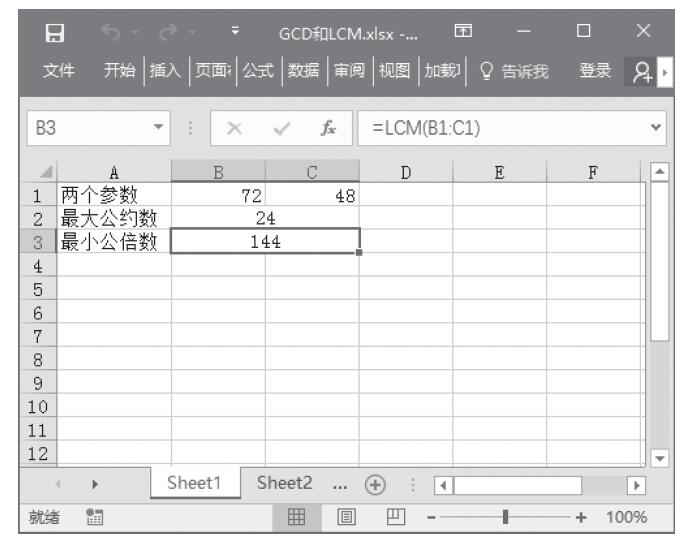
图13-25 计算结果
【使用指南】LCM函数可以用于将分母不同的分数相加。对两函数来说,如果参数为非数值型,则两函数都将返回错误值“#VALUE!”。如果参数小于零,则两函数都将返回错误值“#NUM!”。