“双样本t-检验”分析工具基于每个样本检验样本总体平均值是否相等。这三个工具分别使用不同的假设:样本总体方差相等、样本总体方差不相等、两个样本代表处理前后同一对象上的观察值。
对于以下所有三个工具,t-统计值t被计算并在输出表中显示为“t Stat”。数据决定了t是负值还是非负值。假设基于相等的基础总体平均值,如果t<0,则“P(T≤t)单尾”返回t-统计的观察值比t更趋向负值的概率。如果t≥0,则“P(T≤t)单尾”返回t-统计的观察值比t更趋向正值的概率。“t单尾临界值”返回截止值,这样,t-统计的观察值将大于或等于“t单尾临界值”的概率就为Alpha。
“P(T≤t)双尾”返回将被观察的t-统计的绝对值大于t的概率。“P双尾临界值”返回截止值,这样,被观察的t-统计的绝对值大于“P双尾临界值”的概率就为Alpha。
t-检验:平均值的成对二样本分析
当样本中存在自然配对的观察值时(例如,对一个样本组在实验前后进行了两次检验),可以使用此成对检验。此分析工具及其公式可以进行成对双样本学生t-检验,以确定取自处理前后的观察值是否来自具有相同总体平均值的分布。此t-检验窗体并未假设两个总体的方差是相等的。
提示:由此工具生成的结果中包含有合并方差,亦即数据相对于平均值的离散值的累积测量值,可以由下面的公式得到。
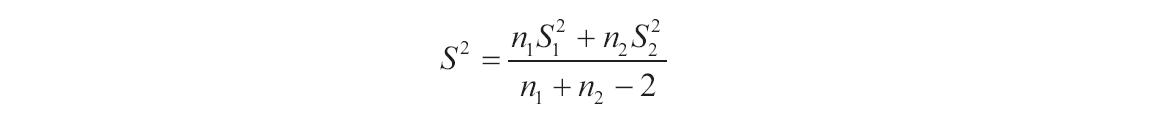
下面通过实例说明如何进行“t-检验:平均值的成对二样本”分析。
步骤1:打开例子工作表,如图22-70所示。
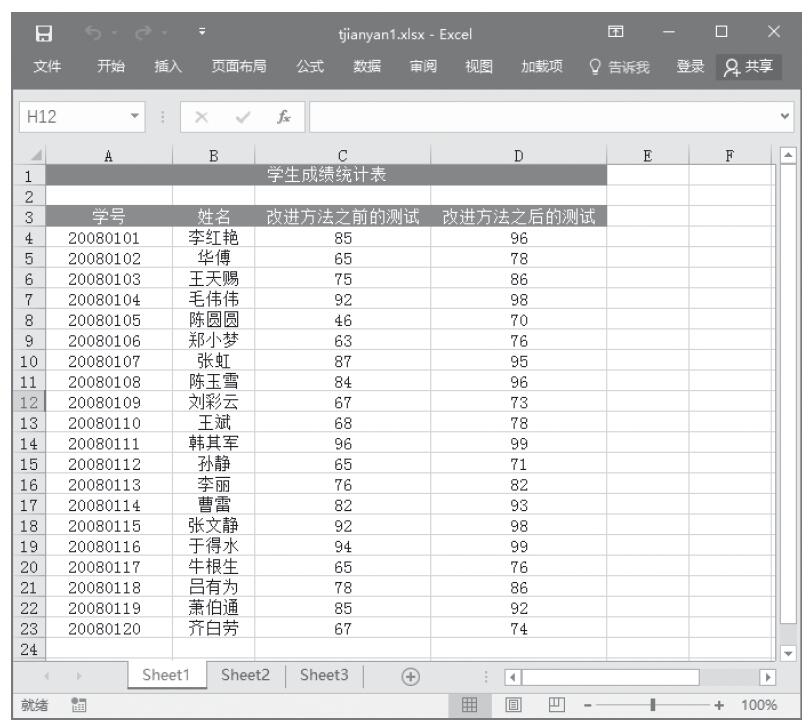
图22-70 例子工作表中的数据
步骤2:单击“数据”选项卡,然后单击“分析”组中的“数据分析”命令,打开“数据分析”对话框。
步骤3:选中“分析工具”列表中的“t-检验:平均值的成对二样本分析”,如图22-71所示。
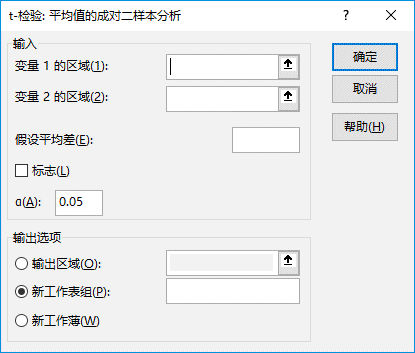
步骤4:单击“确定”按钮,打开“t-检验:平均值的成对二样本分析”对话框。
步骤5:根据需要设置以下选项,具体设置如图22-72所示。其中一些选项简要介绍如下。
图22-71 选中“t-检验:平均值的成对二样本分析”
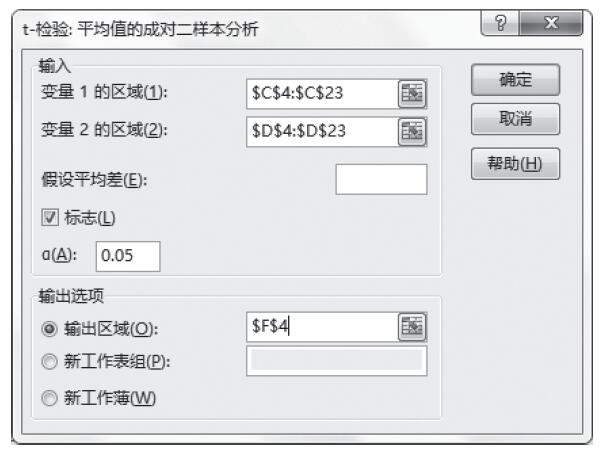
图22-72 设置t-检验:平均值的成对二样本分析选项
- 变量1的区域:在此输入需要分析的第一个数据区域的单元格引用。该区域必须为单行或单列,并且包含与第二个区域相同的数据点。
- 变量2的区域:在此输入需要分析的第二个数据区域的单元格引用。该区域必须为单行或单列,并且包含与第二个区域相同的数据点。
- 假设平均差:输入样本平均值的差值。0(零)值表示假设样本平均值相同。
- α:输入检验的置信度。该值必须介于0到1之间。α置信度为与I型错误发生概率相关的显著性水平(拒绝真假设)。
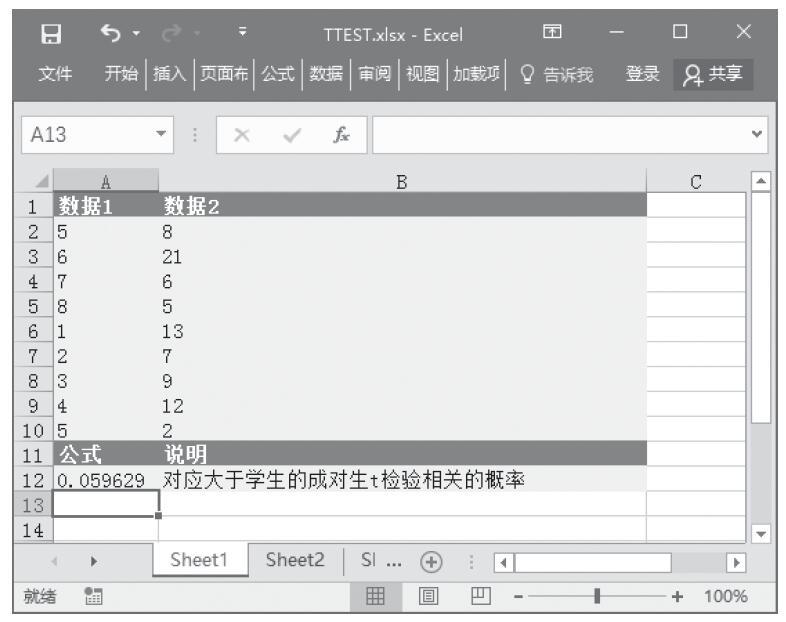
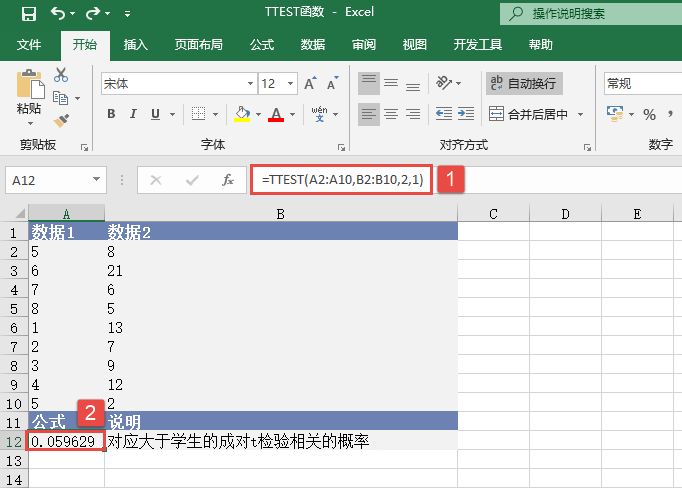
步骤6:单击“确定”按钮,即可看到分析的结果,如图22-73所示。
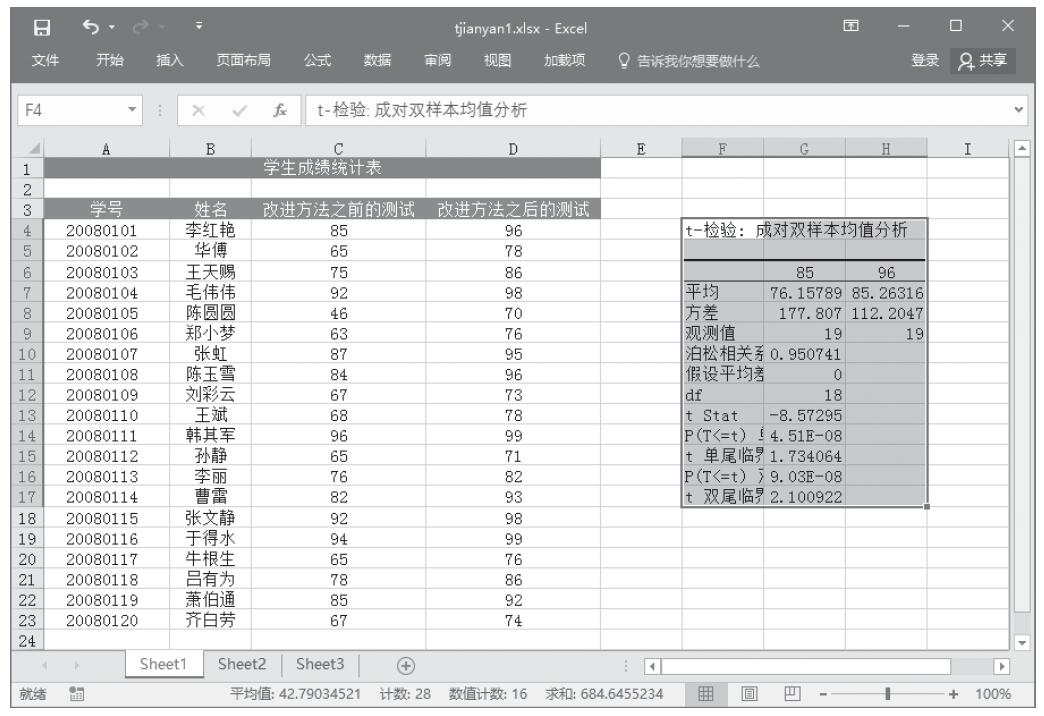
图22-73 t-检验:平均值的成对二样本分析结果
t-检验:双样本等方差假设
本分析工具可进行双样本等方差t-检验。此t-检验窗体假设两个数据集取自具有相同方差的分布,故也称作同方差t-检验。可以使用此t-检验来确定两个样本是否来自具有相同总体平均值的分布。
下面通过实例说明如何进行“t-检验:双样本等方差假设”分析。
步骤1:打开例子工作表,如图22-74所示。
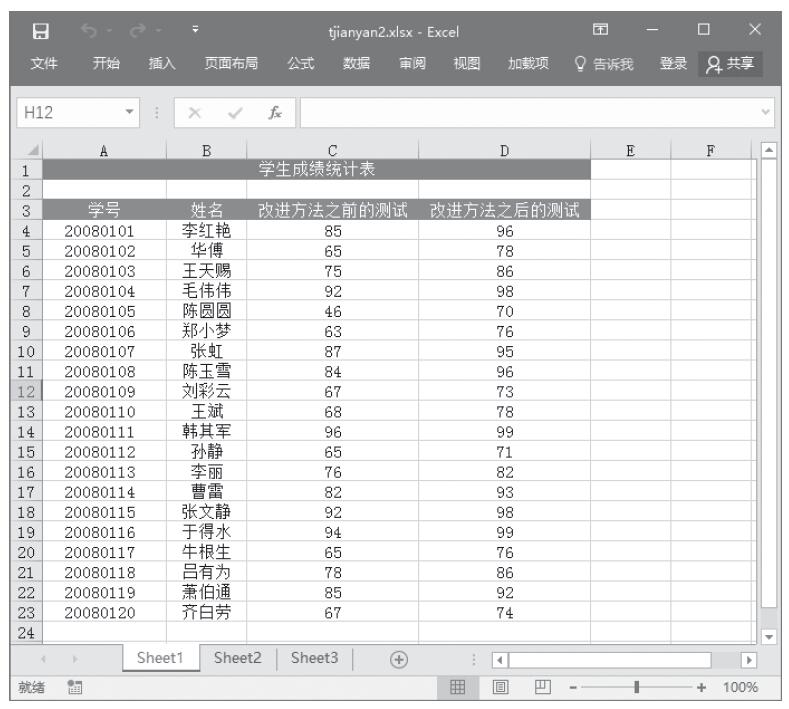
图22-74 例子工作表中的数据
步骤2:单击“数据”选项卡,然后单击“分析”组中的“数据分析”命令,打开“数据分析”对话框。
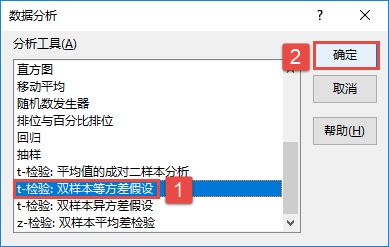
步骤3:选中“分析工具”列表中的“t-检验:双样本等方差假设”,如图22-75所示。
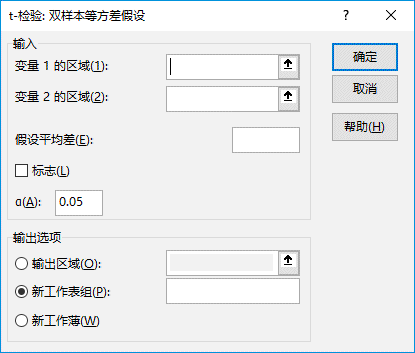
步骤4:单击“确定”按钮,打开“t-检验:双样本等方差假设”对话框。
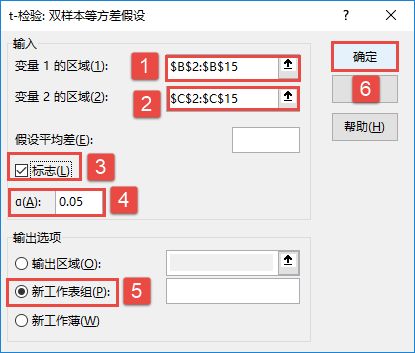
步骤5:根据需要设置各选项,具体设置如图22-76所示。

图22-75 选中“t-检验:双样本等方差假设”
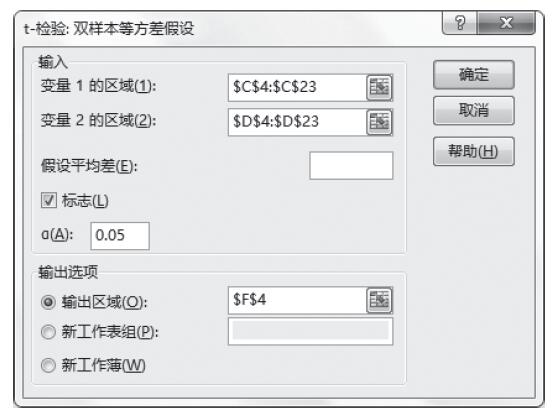
图22-76 设置t-检验:双样本等方差假设选项
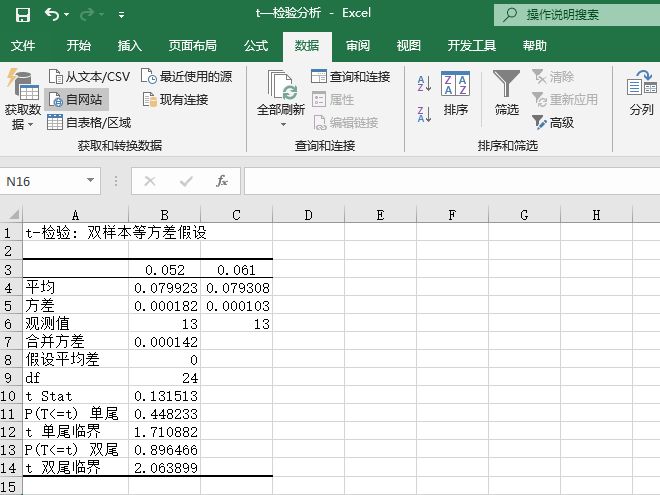
步骤6:单击“确定”按钮,即可看到分析的结果,如图22-77所示。
t-检验:双样本异方差假设
本分析工具可进行双样本异方差t-检验。此t-检验窗体假设两个数据集取自具有不同方差的分布,故也称作异方差t-检验。如同上面的“等方差”情况,可以使用此t-检验来确定两个样本是否来自具有相同总体平均值的分布。当两个样本中有截然不同的对象时,可使用此检验。当对于每个对象具有唯一一组对象以及代表每个对象在处理前后的测量值的两个样本时,应使用下面的示例中所描述的成对检验。
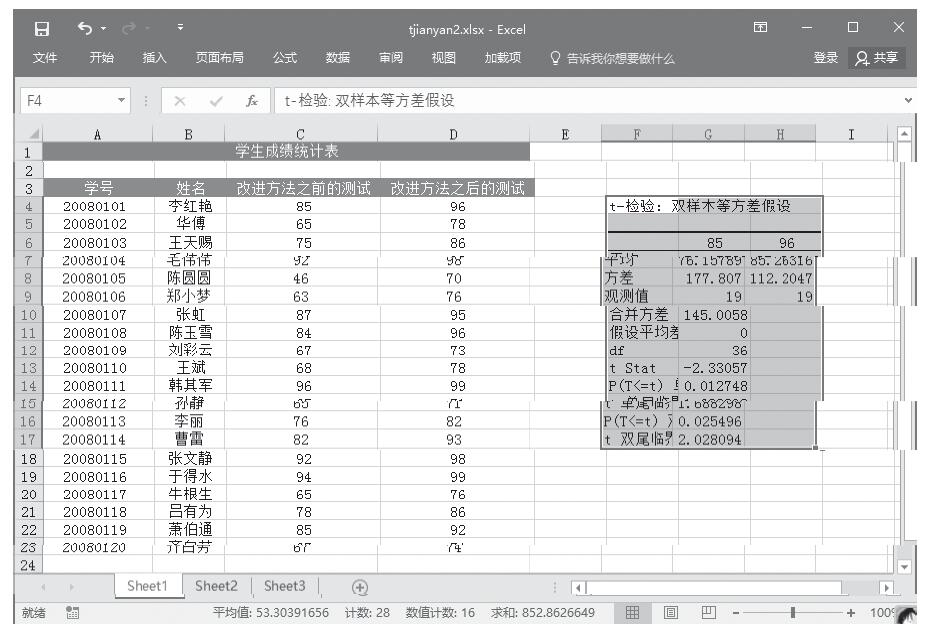
图22-77 t-检验:双样本等方差分析结果
用于确定统计值t的公式如下。
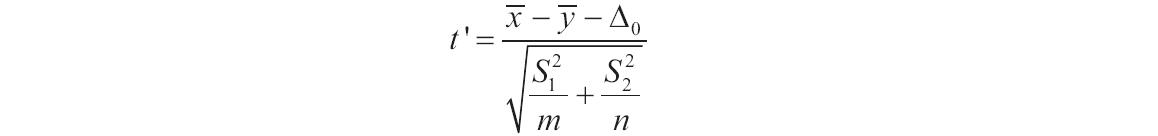
下面的公式可用于计算自由度df。因为计算结果一般不是整数,所以df的值被舍入为最接近的整数以便从t表中获得临界值。因为有可能为TTEST计算出一个带有非整数df的值,所以Excel工作表函数TTEST使用计算出的、未进行舍入的df值。由于这些决定自由度的不同方式,TTEST函数和此t-检验工具的结果将与“异方差”情况中不同。
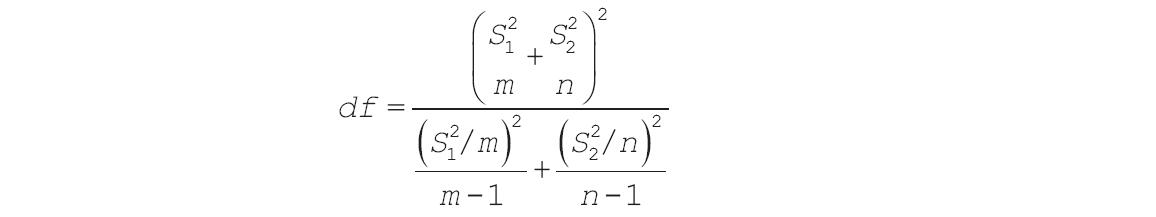
下面通过实例说明如何进行“t-检验:双样本异方差”分析。
步骤1:打开例子工作表,如图22-78所示。
步骤2:单击“数据”选项卡,然后单击“分析”组中的“数据分析”命令,打开“数据分析”对话框。
步骤3:选中“分析工具”列表中的“t-检验:双样本异方差假设”,如图22-79所示。
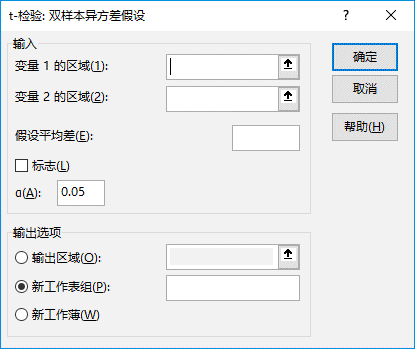
步骤4:单击“确定”按钮,打开“t-检验:双样本异方差假设”对话框。
步骤5:根据需要设置各选项,具体设置如图22-80所示。
步骤6:单击“确定”按钮,即可看到分析的结果,如图22-81所示。
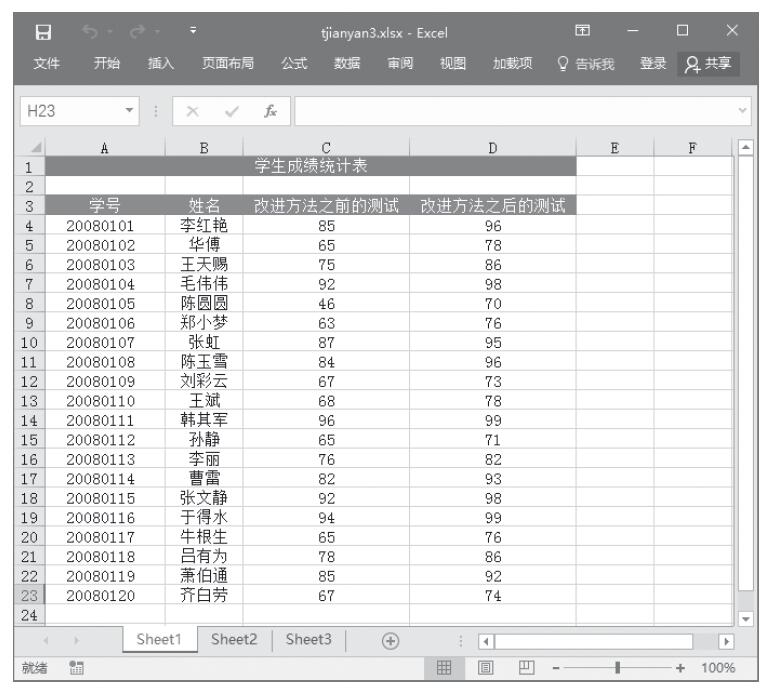
图22-78 例子工作表中的数据

图22-79 选中“t-检验:双样本异方差假设”
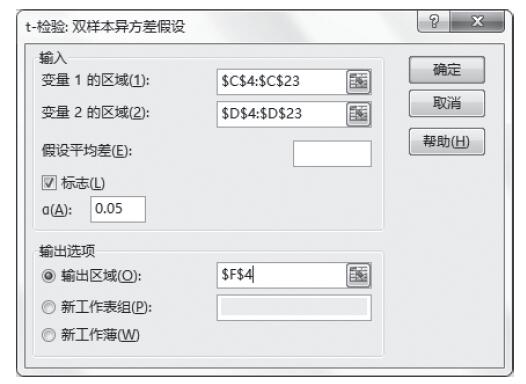
图22-80 设置t-检验:双样本异方差分析选项
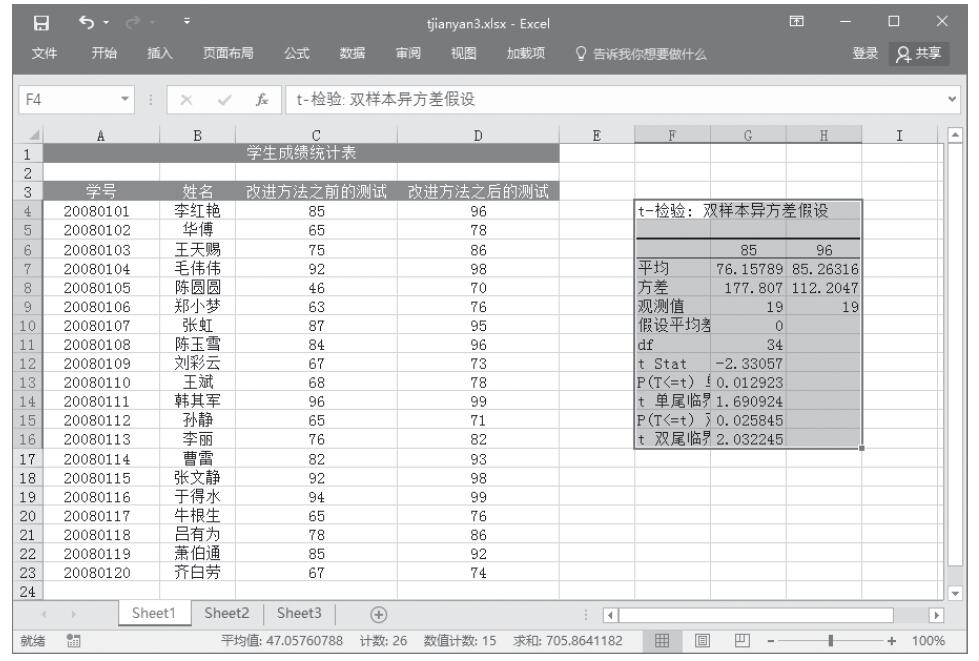
图22-81 t-检验:双样本异方差分析结果