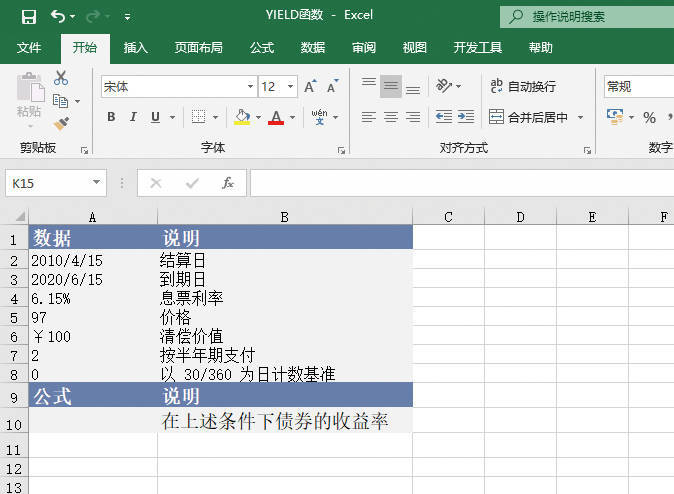
YIELD函数用于计算定期支付利息的证券的收益率。YIELD函数的语法如下。
YIELD(settlement,maturity,rate,pr,redemption,frequency,basis)
其中参数settlement为证券的结算日,即在发行日之后,证券卖给购买者的日期。maturity为有价证券的到期日,即有价证券有效期截止时的日期。rate为有价证券的年息票利率。pr为面值¥100的有价证券的价格。redemption为面值¥100的有价证券的清偿价值。frequency为年付息次数。如果按年支付,frequency=1;按半年期支付,frequency=2;按季支付,frequency=4。basis为日计数基准类型。
典型案例
已知某债券的结算日、到期日、息票利率、价格、清偿价值、支付方式等信息,计算在这些条件下债券的收益率。基础数据如图17-57所示。
步骤1:打开例子工作簿“YIELD.xlsx”。
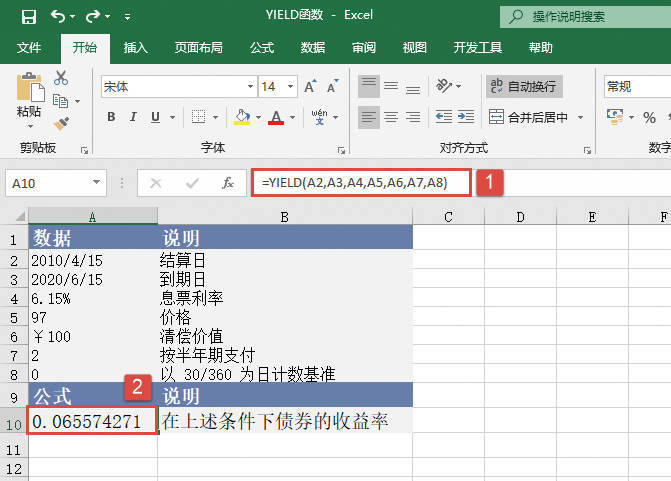
步骤2:在单元格A10中输入公式“=YIELD(A2,A3,A4,A5,A6,A7,A8)”,用于计算在上述条件下债券的收益率。计算结果如图17-58所示。
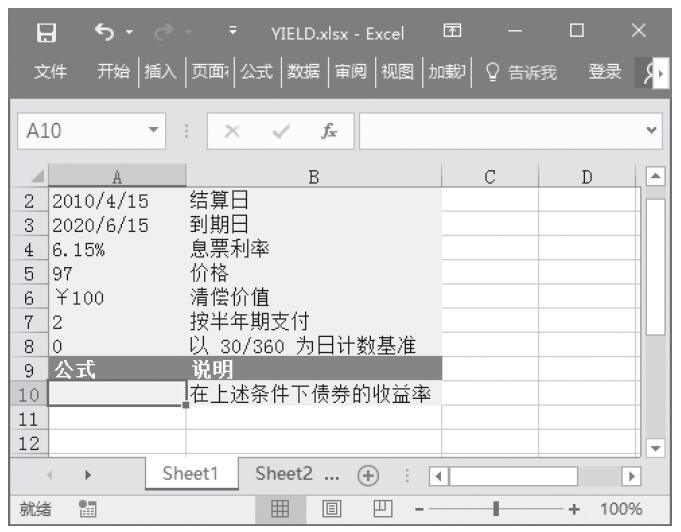
图17-57 基础数据
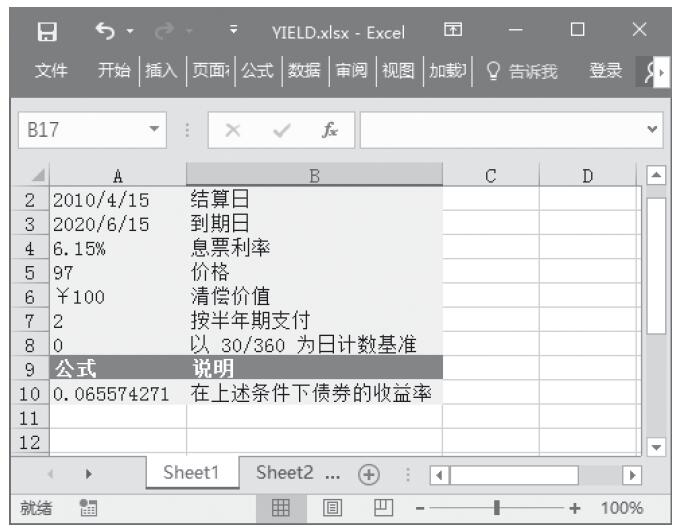
图17-58 计算结果
使用指南
settlement、maturity、frequency和basis若非整数将被截尾取整。如果settlement或maturity不是合法日期,函数YIELD返回错误值“#VALUE!”;如果rate<0,函数YIELD返回错误值“#NUM!”;如果pr≤0或redemption≤0,函数YIELD返回错误值“#NUM!”;如果frequency不为1、2或4,函数YIELD返回错误值“#NUM!”;如果basis<0或basis>4,函数YIELD返回错误值“#NUM!”;如果settlement≥maturity,函数YIELD返回错误值“#NUM!”。
如果在清偿日之前只有一个或是没有付息期间,函数YIELD的计算公式为:

式中:
A为付息期的第一天到结算日之间的天数(应计天数)。
DSR为结算日与清偿日之间的天数。
E为付息期所包含的天数。
如果在redemption之前尚有多个付息期间,则通过100次迭代来计算函数YIELD。基于函数PRICE中给出的公式,并使用牛顿迭代法不断修正计算结果,直到在给定的收益率下的计算价格逼近于实际价格。