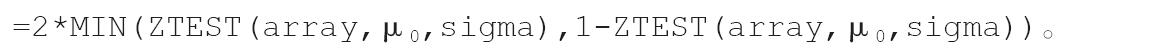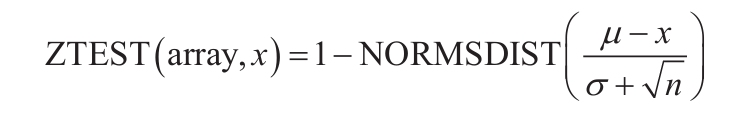z检验 – Excel22

Excel z-检验：双样本平均差检验

“z-检验：双样本平均差检验”分析工具可对具有已知方差的平均值进行双样本z-检验。此工具用于检验两个总体平均值之间不存在差异的空值假设，而不是单方或双方的其他假设。如果方差未知，则应使用工作表函数ZTEST。

当使用“z-检验”工具时，应该仔细理解输出。当总体平均值之间没有差异时，“P（Z≤z）单尾”是P（Z≥ABS（z）），即与z观察值沿着相同的方向远离0的z值的概率。当总体平均值之间没有差异时，“P（Z≤z）双尾”是P（Z≥ABS（z）或Z≤-ABS（z）），即沿着任何方向（而非与观察到的z值的方向一致）远离0的z值的概率。双尾结果只是单尾结果乘以2。z-检验工具还可用于当两个总体平均值之间的差异具有特定非零值的空值假设的情况。例如，可以使用此检验确定两个汽车模型的性能差异。

下面通过实例说明如何进行“z-检验：双样本平均差”分析。

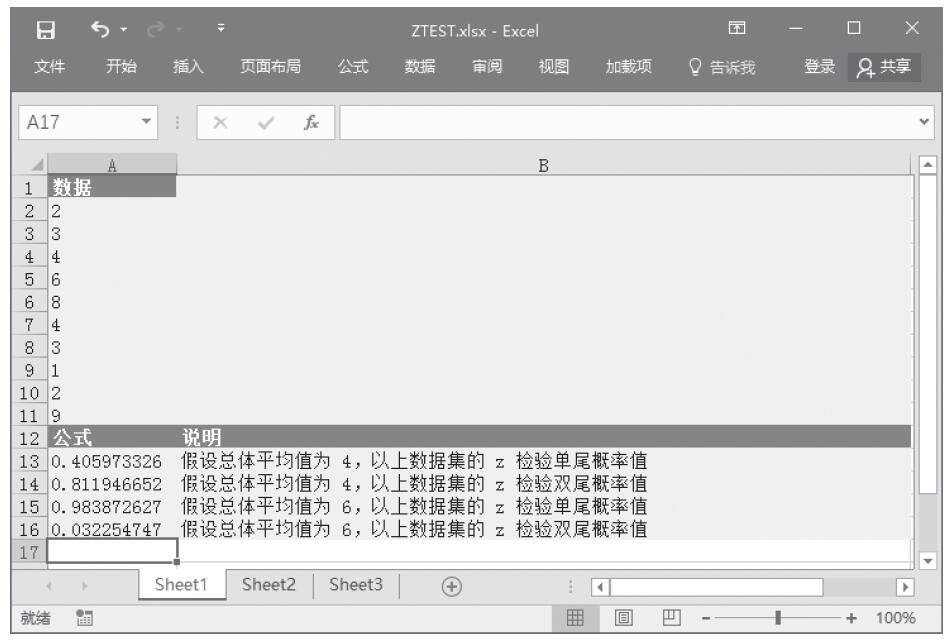
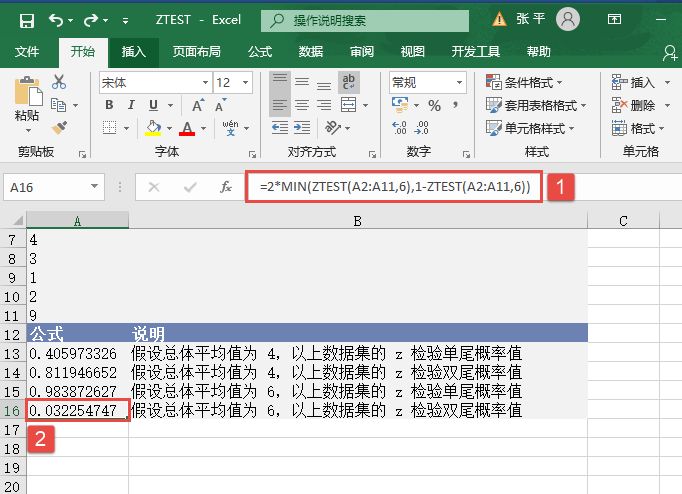
步骤1：打开例子工作表，如图22-82所示。

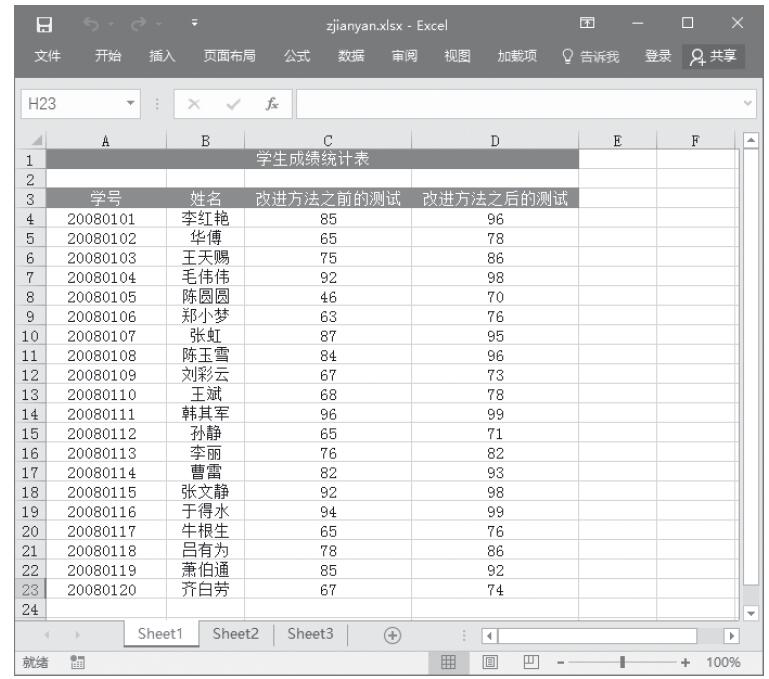
图22-82　例子工作表中的数据

步骤2：单击“数据”选项卡，然后单击“分析”组中的“数据分析”命令，打开“数据分析”对话框。

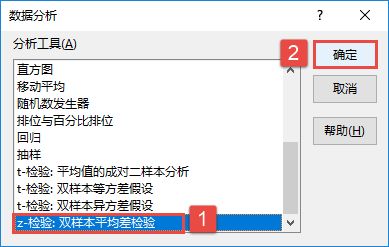
步骤3：选中“分析工具”列表中的“z-检验：双样本平均差检验”，如图22-83所示。

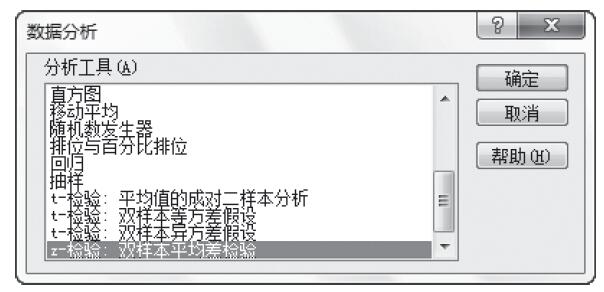
图22-83　选中“t-检验：双样本平均差检验”

步骤4：单击“确定”按钮，打开“z-检验：双样本平均差检验”对话框。

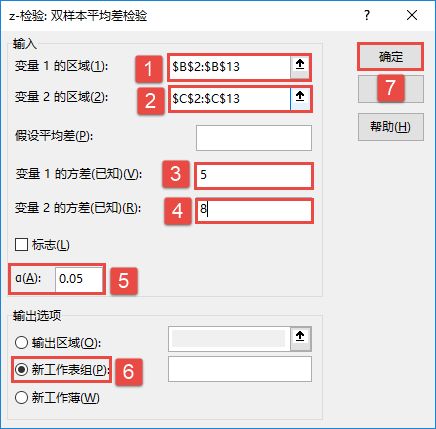
步骤5：根据需要设置各选项，具体设置如图22-84所示。其中一些选项简要介绍如下。

变量1的方差（已知）：输入已知变量1输入区域的总体方差。
变量2的方差（已知）：输入已知变量2输入区域的总体方差。

步骤6：单击“确定”按钮，即可看到分析的结果，如图22-85所示。

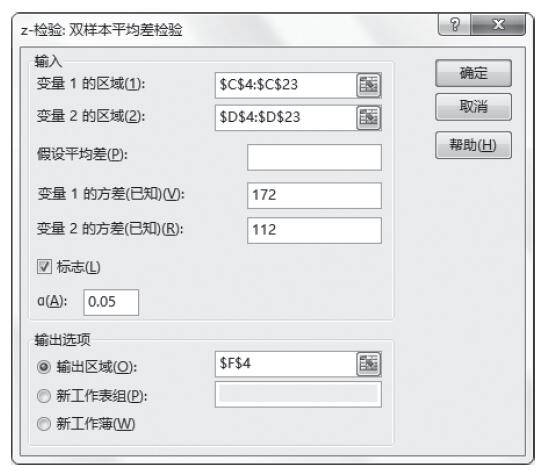
图22-84　设置z-检验：双样本平均差检验分析选项

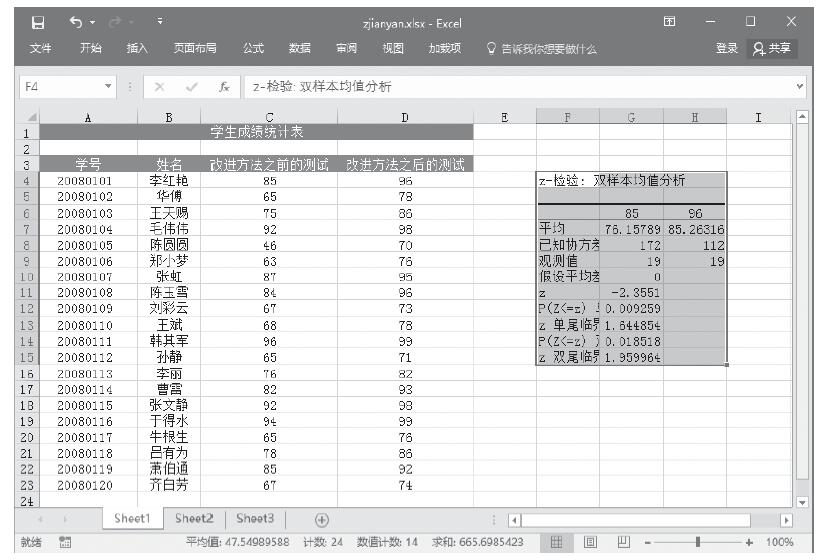
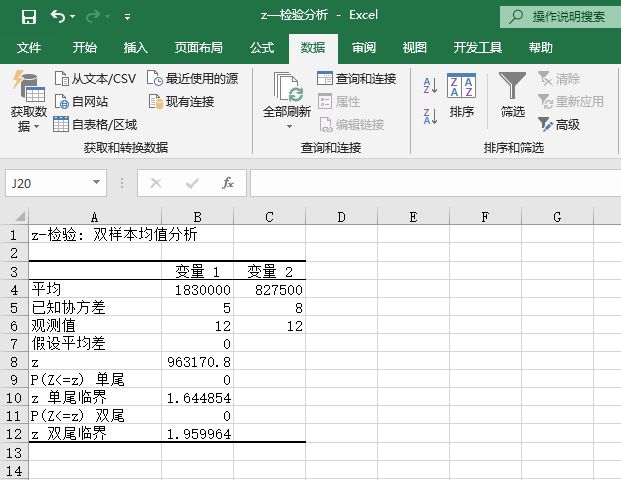
图22-85　z-检验：双样本平均差检验分析结果

Excel 应用ZTEST函数计算z检验的单尾概率值

ZTEST函数用于计算z检验的单尾概率值。对于给定的假设总体平均值μ₀，ZTEST返回样本平均值大于数据集（数组）中观察平均值的概率，即观察样本平均值。ZTEST函数的语法如下。

其中参数array为用来检验μ₀的数组或数据区域。μ₀为被检验的值。sigma为样本总体（已知）的标准偏差，如果省略，则使用样本标准偏差。

【典型案例】已知一组数据，计算z检验的单尾概率值。基础数据如图16-45所示。

步骤1：打开例子工作簿“ZTEST.xlsx”。

步骤2：在单元格A13中输入公式“=ZTEST（A2：A11，4）”，用于计算总体平均值为4时数据集的z检验单尾概率值。

步骤3：在单元格A14中输入公式“=2*MIN（ZTEST（A2：A11，4），1-ZTEST（A2：A11，4））”，用于计算总体平均值为4时数据集的z检验双尾概率值。

步骤4：在单元格A15中输入公式“=ZTEST（A2：A11，6）”，用于计算总体平均值为6时数据集的z检验单尾概率值。

步骤5：在单元格A16中输入公式“=2*MIN（ZTEST（A2：A11，6），1-ZTEST（A2：A11，6））”，用于计算假设总体平均值为6，以上数据集的z检验双尾概率值。计算结果如图16-46所示。

图16-45　基础数据

图16-46　计算结果

【使用指南】如果array为空，函数ZTEST返回错误值“#N/A”。不省略sigma时，函数ZTEST的计算公式如下：

省略sigma时，函数ZTEST的计算公式如下：

其中，x为样本平均值AVERAGE（array）；s为样本标准偏差STDEV（array）；n为样本中的观察值个数COUNT（array）。

ZTEST表示当基础总体平均值为μ₀时，样本平均值大于观察值AVERAGE（array）的概率。由于正态分布是对称的，如果AVERAGE（array）＜μ₀，则ZTEST的返回值将大于0.5。

当基础总体平均值为μ₀，样本平均值从μ₀（沿任一方向）变化到AVERAGE（array）时，下面的Excel公式可用于计算双尾概率。

Excel 计算z检验的单尾概率值：ZTEST函数

ZTEST函数用于计算z检验的单尾概率值。对于给定的假设总体平均值μ0，ZTEST返回样本平均值大于数据集（数组）中观察平均值的概率，即观察样本平均值。ZTEST函数的语法如下：

ZTEST(array,μ0,sigma)

其中，array参数为用来检验μ₀的数组或数据区域，μ0参数为被检验的值，sigma参数为样本总体（已知）的标准偏差，如果省略，则使用样本标准偏差。下面通过实例详细讲解该函数的使用方法与技巧。

打开“ZTEST.xlsx”工作簿，切换至“Sheet1”工作表，本例中的原始数据如图17-25所示。工作表中记录了一组数据，要求根据工作表中的数据计算出z检验的概率值。具体的操作步骤如下。

图17-25　原始数据

STEP01：选中A13单元格，在编辑栏中输入公式“=ZTEST(A2:A11,4)”，用于计算总体平均值为4时数据集的z检验单尾概率值，输入完成后按“Enter”键返回计算结果，如图17-26所示。

STEP02：选中A14单元格，在编辑栏中输入公式“=2*MIN(ZTEST(A2:A11,4),1-ZTEST(A2:A11,4))”，用于计算总体平均值为4时数据集的z检验双尾概率值，输入完成后按“Enter”键返回计算结果，如图17-27所示。

STEP03：选中A15单元格，在编辑栏中输入公式“=ZTEST(A2:A11,6)”，用于计算总体平均值为6时数据集的z检验单尾概率值，输入完成后按“Enter”键返回计算结果，如图17-28所示。

图17-26　计算z检验单尾概率值（一）

图17-27　计算z检验双尾概率值（一）

STEP04：选中A16单元格，在编辑栏中输入公式“=2*MIN(ZTEST(A2:A11,6),1-ZTEST(A2:A11,6))”，用于计算总体平均值为6时数据集的z检验双尾概率值，输入完成后按“Enter”键返回计算结果，如图17-29所示。

图17-28　计算z检验单尾概率值（二）

图17-29　计算z检验双尾概率值（二）

如果array为空，函数ZTEST返回错误值“#N/A”。不省略sigma时，函数ZTEST的计算公式如下：

省略sigma时，函数ZTEST的计算公式如下：

其中，x为样本平均值AVERAGE(array)；s为样本标准偏差STDEV(array)；n为样本中的观察值个数COUNT(array)。

ZTEST表示当基础总体平均值为μ₀时，样本平均值大于观察值AVERAGE(array)的概率。由于正态分布是对称的，如果AVERAGE(array)<μ₀，则ZTEST的返回值将大于0.5。

当基础总体平均值为μ₀，样本平均值从μ₀（沿任一方向）变化到AVERAGE(array)时，下面的Excel公式可用于计算双尾概率：

=2*MIN(ZTEST(array,μ0,sigma),1-ZTEST(array,μ0,sigma))

Excel 2019 z-检验分析图解

z-检验工具对具有已知方差的平均值进行双样本z-检验。通过使用z-检验工具，可以检验两个总体平均值之间不存在差异的空值假设，而不是单方或双方的其他假设。而且，也可以使用z-检验确定两个汽车模型的性能差异。下面通过具体实例来详细讲解利用z-检验分析数据的操作技巧。

已知某公司两个部门的收入数据，使用“双样本平均差检验”分析工具对两个部门的收入数据进行分析，分析两个部门收入情况有无明显差异，具体操作步骤如下。

STEP01：打开“z-检验分析.xlsx”工作簿，切换至“数据”选项卡，然后在“分析”组中单击“数据分析”按钮，打开如图7-105所示的“数据分析”对话框。在“分析工具”列表框中选择“z-检验：双样本平均差检验”选项，然后单击“确定”按钮。

图7-105　选择双样本平均差检验分析工具

STEP02：随后会打开“z-检验:双样本平均差检验”对话框，在“输入”列表区域设置变量1的区域为“$B$2:$B$13”，设置变量2的区域为“$C$2:$C$13”，设置变量1的方差为“5”，变量2的方差为“8”，并设置α的值为“0.05”，然后在“输出选项”列表中单击选中“新工作表组”单选按钮，最后单击“确定”按钮即可，如图7-106所示。

STEP03：此时，工作表中会显示“z-检验:双样本平均差检验”的分析结果，如图7-107所示。

图7-106　设置属性

图7-107　z-检验分析结果