相册 – 第4页

Excel 抽样分析图解

“抽样”分析工具以数据源区域为总体，从而为其创建一个样本。当总体太大而不能进行处理或绘制时，可以选用具有代表性的s样本。如果确认数据源区域中的数据是周期性的，还可以仅对一个周期中特定时间段中的数值进行采样。例如，如果数据源区域包含季度销售量数据，则以“四”为周期进行采样，将在输出区域中生成与数据源区域中相同季度的数值。

下面通过实例说明如何进行抽样分析。

步骤1：打开例子工作表，如图22-66所示。

图22-66　例子工作表中的数据

步骤2：单击“数据”选项卡，然后单击“分析”组中的“数据分析”命令，打开“数据分析”对话框。

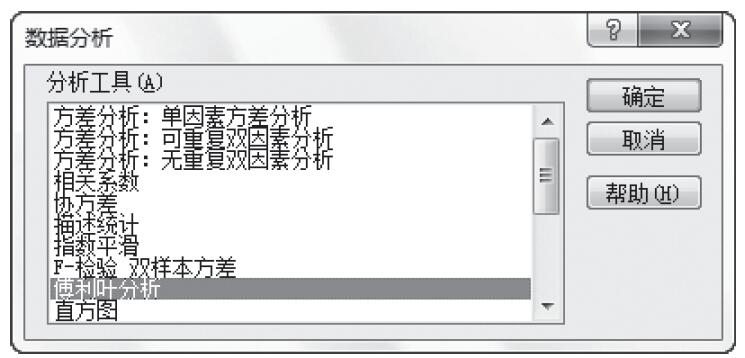
步骤3：选中“分析工具”列表中的“抽样”，如图22-67所示。

步骤4：单击“确定”按钮，打开“抽样”对话框。

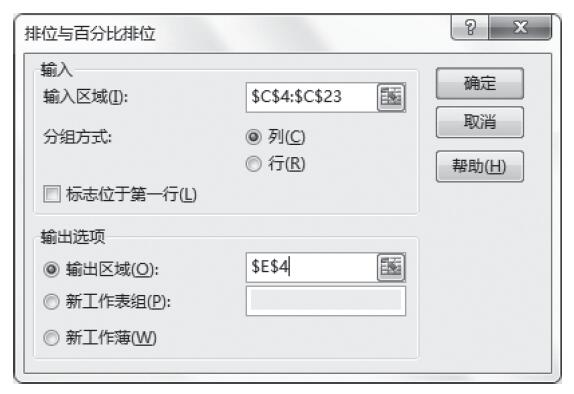
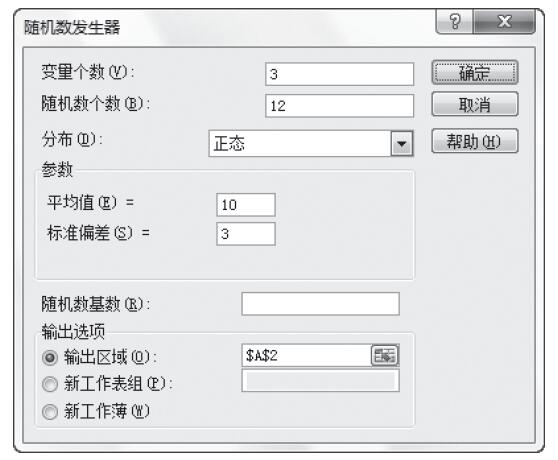
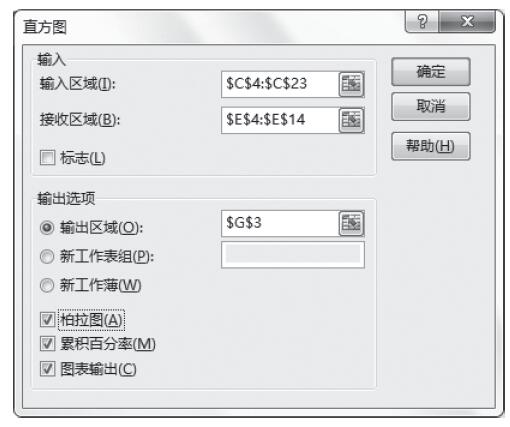
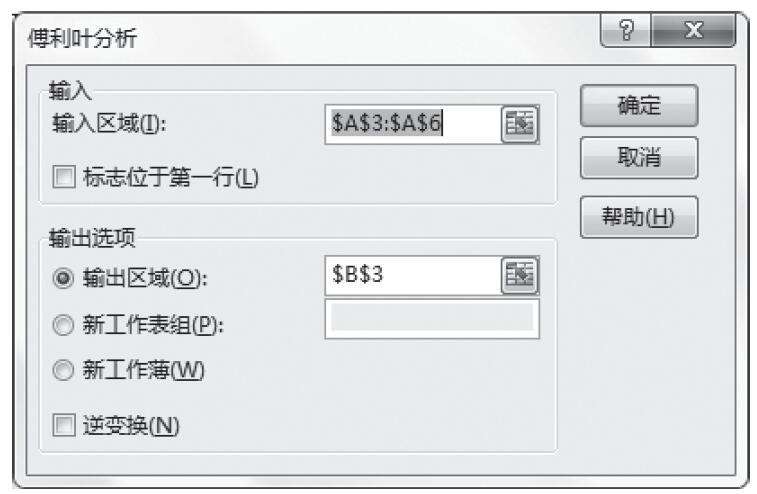
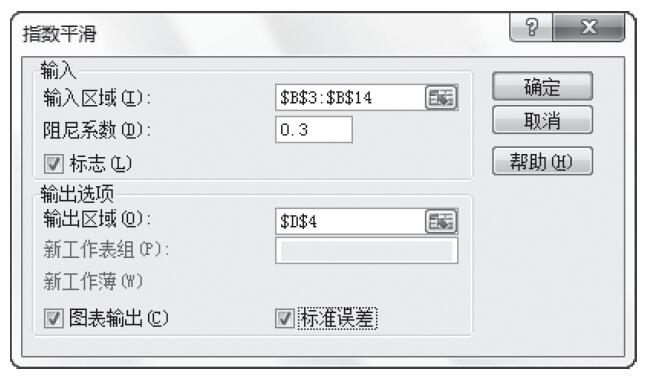
步骤5：根据需要设置以下选项，具体设置如图22-68所示。其中一些选项简要介绍如下。

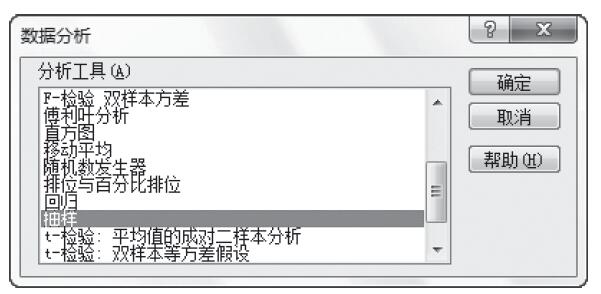
图22-67　选中“分析工具”列表中的“抽样”

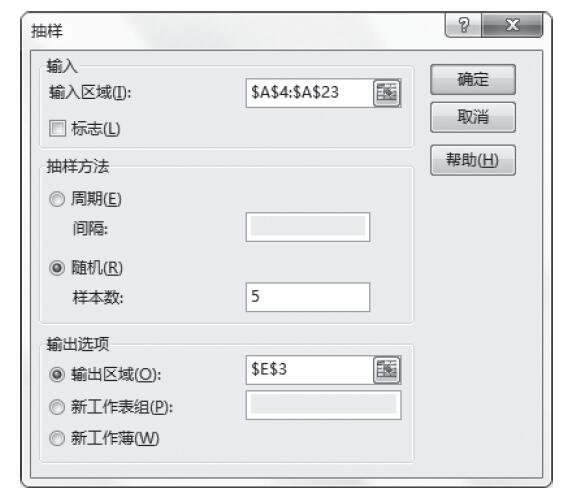
图22-68　设置抽样选项

输入区域：输入数据区域引用，该区域中包含需要进行抽样的总体数据。Excel先从第一列中抽取样本，然后是第二列，等等。
抽样方法：单击“周期”或“随机”可指明所需的抽样间隔。
间隔：输入进行抽样的周期间隔。输入区域中位于间隔点处的数值以及此后每一个间隔点处的数值将被复制到输出列中。当到达输入区域的末尾时，抽样将停止。
样本数：输入需要在输出列中显示的随机数的个数。每个数值是从输入区域中的随机位置上抽取出来的，而且任何数值都可以被多次抽取。
输出区域：输入对输出表左上角单元格的引用。所有数据均将写在该单元格下方的单列里。如果选择的是“周期”，则输出表中数值的个数等于输入区域中数值的个数除以“间隔”。如果选择的是“随机”，则输出表中数值的个数等于“样本数”。

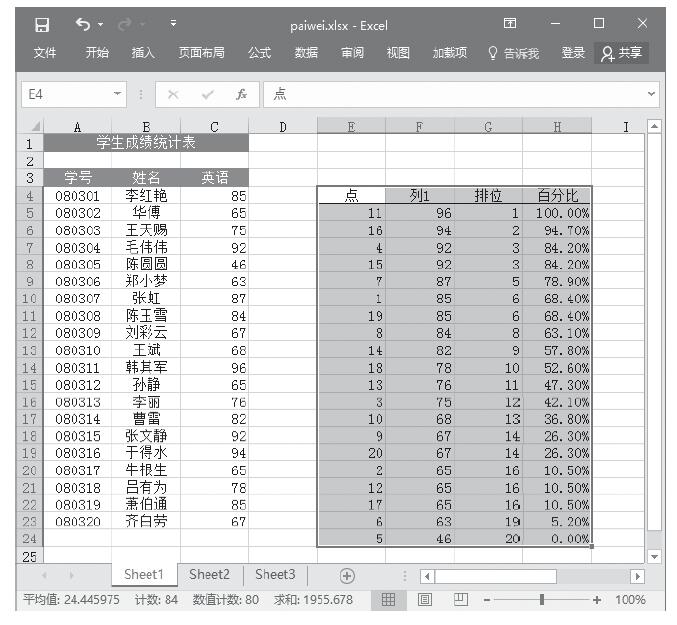
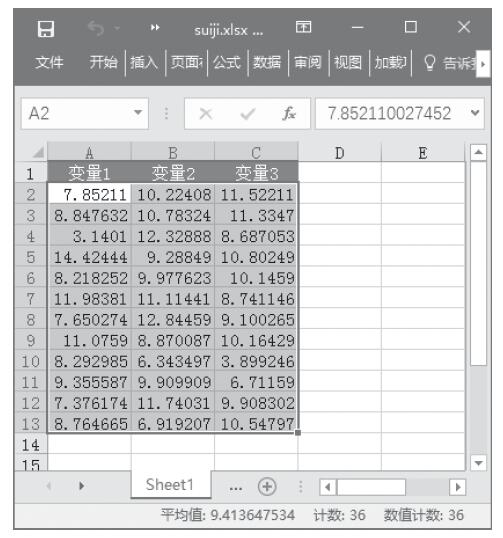
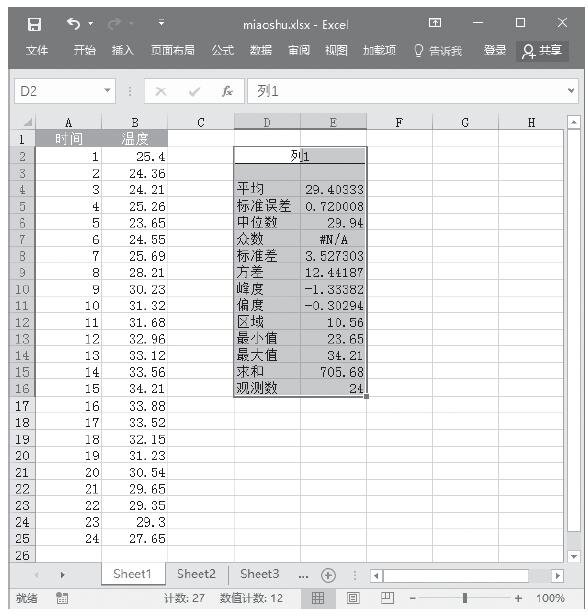
步骤6：单击“确定”按钮，即可看到分析的结果，如图22-69所示。

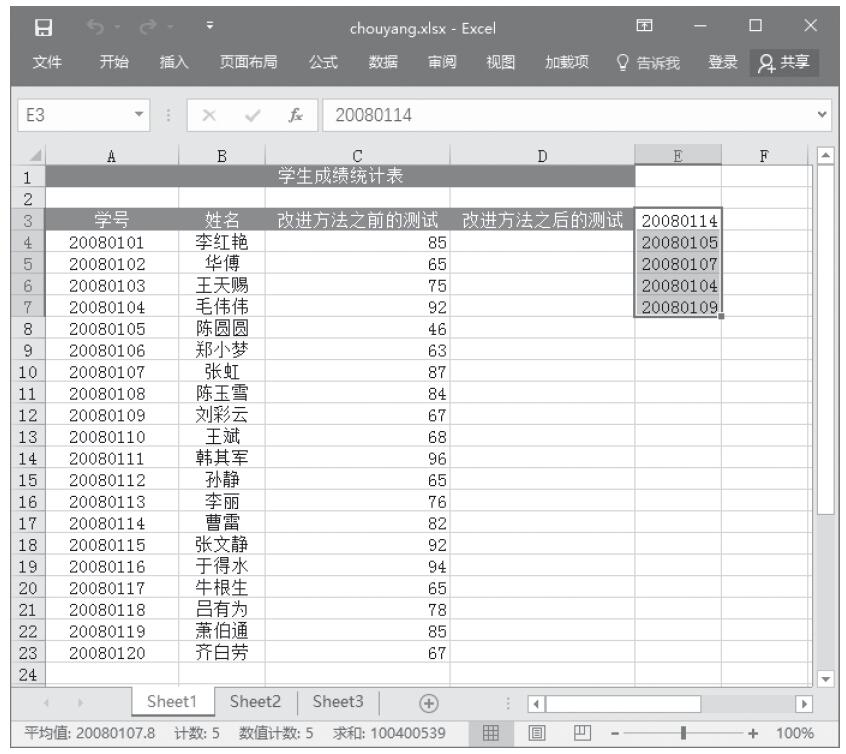
图22-69　抽样分析结果（输出表）

Excel 回归分析图解

“回归”分析工具通过对一组观察值使用“最小二乘法”直线拟合来执行线性回归分析。本工具可用来分析单个因变量是如何受一个或几个自变量的值影响的。例如，观察某个运动员的运动成绩与一系列统计因素（如年龄、身高和体重等）的关系。可以基于一组已知的成绩统计数据，确定这三个因素分别在运动成绩测试中所占的比重，然后使用该结果对尚未进行过测试的运动员的表现进行预测。“回归”工具使用工作表函数LINEST。

图22-64　例子工作表中的数据

下面通过实例说明如何进行回归分析。

步骤1：打开例子工作表，如图22-64所示。

步骤2：单击“数据”选项卡，然后单击“分析”组中的“数据分析”命令，打开“数据分析”对话框。

步骤3：选中“分析工具”列表中的“回归”，如图22-65所示。

图22-65　选中“分析工具”列表中的“回归”

步骤4：单击“确定”按钮，打开“回归”对话框。

步骤5：根据需要设置以下选项。

·Y值输入区域：输入对因变量数据区域的引用，该区域必须由单列数据组成。

·X值输入区域：输入对自变量数据区域的引用，Excel将对此区域中的自变量从左到右进行升序排列。自变量的个数最多为16。

·置信度：如果需要在汇总输出表中包含附加的置信度信息，则选中此复选框。在右侧的框中输入所要使用的置信度，默认值为95%。

·常数为零：如果要强制回归线经过原点，则选中此复选框。

·输出区域：输入对输出表左上角单元格的引用。汇总输出表至少需要有七列，其中包括方差分析表、系数、y估计值的标准误差、r2值、观察值个数以及系数的标准误差。

·残差：如果需要在残差输出表中包含残差，则选中此复选框。

·标准残差：如果需要在残差输出表中包含标准列差，则选中此复选框。

·残差图：如果需要为每个自变量及其残差生成一张图表，则选中此复选框。

·线性拟合图：如果需要为预测值和观察值生成一张图表，则选中此复选框。

·正态概率图：如果需要生成一张图表来绘制正态概率，则选中此复选框。

Excel 排位与百分比排位应用图解

“排位与百分比排位”分析工具可以产生一个数据表，在其中包含数据集中各个数值的顺序排位和百分比排位，用来分析数据集中各数值间的相对位置关系。该工具使用工作表函数RANK和PERCENT-RANK。RANK不考虑重复值。如果希望考虑重复值，则在使用工作表函数RANK的同时，使用帮助文件中所建议的函数RANK的修正因素。

下面通过实例说明如何进行排位与百分比排位分析。

步骤1：打开例子工作表，其中包含预先输入的要处理的数据，如图22-60所示。

步骤2：单击“数据”选项卡，然后单击“分析”组中的“数据分析”命令，打开“数据分析”对话框。

步骤3：选中“分析工具”列表中的“排位与百分比排位”，如图22-61所示。

图22-60　例子工作表中的数据

图22-61　选中“分析工具”列表中的“排位与百分比排位”

步骤4：单击“确定”按钮，打开“排位与百分比排位”对话框。

步骤5：根据需要设置各选项，具体设置如图22-62所示。

步骤6：单击“确定”按钮，即可看到分析的结果，如图22-63所示。

图22-62　设置排位与百分比排位选项

图22-63　排位与百分比排位分析结果

Excel 随机数发生器应用图解

“随机数发生器”分析工具可用几个分布之一产生的独立随机数来填充某个区域。可以通过概率分布来表示一组数据的总体特征。例如，可以使用正态分布来表示人体身高的总体特征，或者使用双值输出的伯努利分布来表示掷币实验结果的总体特征。

下面通过实例说明如何进行随机数发生器分析。

步骤1：打开例子工作表，如图22-56所示。

步骤2：单击“数据”选项卡，然后单击“分析”组中的“数据分析”命令，打开“数据分析”对话框。

步骤3：选中“分析工具”列表中的“随机数发生器”，如图22-57所示。

图22-56　输入将要处理的数据

图22-57　选中“分析工具”列表中的“随机数发生器”

步骤4：单击“确定”按钮，打开“随机数发生器”对话框。

步骤5：根据需要设置以下选项，具体设置如图22-58所示。其中一些选项简要介绍如下。

图22-58　设置随机数发生器选项

随机数个数：在此输入要查看的数据点个数。每一个数据点出现在输出表的一行中。如果没有输入数字，Excel会在指定的输出区域中填充所有的行。
分布：在此选择用于创建随机数的分布方法。
均匀：以下限和上限来表征。其变量是通过对区域中的所有数值进行等概率抽取而得到的。普通的应用是在范围0到1之间的均匀分布。Excel 2016共提供了7种随机数的分布方法，分别为均匀、正态、伯努利、二项式、泊松、模式和离散。
正态：以平均值和标准偏差来表征。普通的应用是平均值为0，标准偏差为1的标准正态分布。
伯努利：以给定的试验中成功的概率（p值）来表征。伯努利随机变量的值为0或1。例如，可以在范围0到1之间抽取均匀分布随机变量。如果变量小于或等于成功的概率，则伯努利随机变量的值为1，否则，随机变量的值为0。
二项式：以一系列试验中成功的概率（p值）来表征。例如，可以按照“试验次数”框中指定的个数生成一系列伯努利随机变量，这些变量之和为一个二项式随机变量。
泊松：以值λ来表征，λ等于平均值的倒数。泊松分布经常用于表示单位时间内事件发生的次数，例如，汽车到达收费停车场的平均速率。
模式：以上界和下界、步长、数值重复率以及序列重复率来表征。
离散：以数值及相应的概率区域来表征。在本对话框中给定的输入区域必须包含两列，左边一列包含数值，右边一列为与数值对应的发生概率。所有概率的和必须为1。
参数：在此输入用于表征选定分布的数值。
随机数基数：在此输入用来构造随机数的可选数值。可以在以后重新使用该数值来生成相同的随机数。

步骤6：单击“确定”按钮，即可看到分析的结果，如图22-59所示。

图22-59　随机数发生器分析结果

Excel 移动平均应用图解

“移动平均”分析工具可以基于特定的过去某段时期中变量的平均值，对未来值进行预测。移动平均值提供了由所有历史数据的简单的平均值所代表的趋势信息。使用此工具可以预测销售量、库存或其他趋势。

下面通过实例说明如何进行移动平均分析。

步骤1：将要处理的数据按图22-52所示输入到工作表中。

图22-52　输入将要处理的数据

步骤2：单击“数据”选项卡，然后单击“分析”组中的“数据分析”命令，打开“数据分析”对话框。

步骤3：选中“分析工具”列表中的“移动平均”，如图22-53所示。

步骤4：单击“确定”按钮，打开“移动平均”对话框。

步骤5：根据需要设置以下选项，具体设置如图22-54所示。其中一些选项简要介绍如下。

输入区域：在此输入待分析数据区域的单元格引用。该区域必须由包含4个或4个以上的数据单元格的单列组成。

间隔：在此输入需要在移动平均计算中包含的数值个数。默认间隔为3。

输出区域：在此输入对输出表左上角单元格的引用。如果选中了“标准误差”复选框，Excel将生成一个两列的输出表，其中右边的一列为标准误差值。如果没有足够的历史数据来设计预测或计算标准误差值，Excel会返回错误值“#N/A”。输出区域必须与输入区域中使用的数据位于同一张工作表中，因此，“新工作表组”和“新工作簿”选项均不可用。

图表输出：选中此复选框可以在输出表中生成一个嵌入直方图。

标准误差：如果要在输出表的一列中包含标准误差值，则选中此复选框。如果只需要单列输出表而不包含标准误差值，则清除此复选框。

步骤6：单击“确定”按钮，即可看到分析的结果，如图22-55所示。

图22-53　选中“分析工具”列表中的“移动平均”

图22-54　设置移动平均选项

图22-55　移动平均分析结果

Excel 直方图应用图解

“直方图”分析工具可计算数据单元格区域和数据接收区间的单个和累积频率。此工具可用于统计数据集中某个数值出现的次数。

例如，在一个有20名学生的班里，可按字母评分的分类来确定成绩的分布情况。直方图表可给出字母评分的边界，以及在最低边界和当前边界之间分数出现的次数。出现频率最多的分数即为数据集中的众数。

下面通过实例说明如何进行直方图分析。

步骤1：将要处理的数据按图22-48所示输入到工作表中。

图22-48　输入将要处理的数据

步骤2：单击“数据”选项卡，然后单击“分析”组中的“数据分析”命令，打开“数据分析”对话框。

步骤3：选中“分析工具”列表中的“直方图”，如图22-49所示。

步骤4：单击“确定”按钮，打开“直方图”对话框。

图22-49　选中“分析工具”列表中的“直方图”

图22-50　设置直方图选项

步骤5：根据需要设置以下选项，具体设置如图22-50所示。其中一些不同于其他分析工具的选项简要介绍如下。

接收区域（可选）：在此输入接收区域的单元格引用，该区域包含一组可选的用来定义接收区域的边界值。这些值应当按升序排列。Excel将统计在当前边界值和相邻边界值之间的数据点个数（如果存在）。如果数值等于或小于边界值，则该值将被归到以该边界值为上限的区域中进行计数。所有小于第一个边界值的数值将一同计数，同样所有大于最后一个边界值的数值也将一同计数。

柏拉图：选中此复选框可以在输出表中按降序来显示数据。如果此复选框被清除，Excel将只按升序来显示数据并省略最右边包含排序数据的三列数据。

累积百分率：选中此复选框可以在输出表中生成一列累积百分比值，并在直方图中包含一条累积百分比线。如果清除此选项，则会省略累积百分比。

图表输出：选中此复选框可以在输出表中生成一个嵌入直方图。

步骤6：单击“确定”按钮，即可看到分析的结果，如图22-51所示。

图22-51　直方图分析结果

Excel 傅里叶分析

“傅里叶分析”分析工具可以解决线性系统问题，并能通过快速傅里叶变换（FFT）进行数据变换来分析周期性的数据。此工具也支持逆变换，即通过对变换后的数据的逆变换返回初始数据。

下面通过实例说明如何进行傅里叶分析。

步骤1：将要处理的数据按图22-43所示输入到工作表中。

步骤2：单击“数据”选项卡，然后单击“分析”组中的“数据分析”命令，打开“数据分析”对话框。

步骤3：选中“分析工具”列表中的“傅里叶分析”，如图22-44所示。

图22-43　输入将要处理的数据

图22-44　选中“分析工具”列表中的“傅里叶分析”

步骤4：单击“确定”按钮，打开“傅里叶分析”对话框。

步骤5：根据需要设置以下选项，具体设置如图22-45所示。其中一些不同于其他分析工具的选项简要介绍如下。

输入区域：在此输入对需要进行变换的实数或复数单元格区域的引用。得数必须表示为“x+yi”或“x+yj”的格式。输入区域中数值的个数必须为2的偶数次幂。如果x为负数，则在前面加上一个撇号（′）。数值的最大个数为4096。

逆变换：如果选中此复选框，则输入区域中的数据将会被认为是经过变换后的数据，并对其进行逆变换，返回初始输入值；如果清除此复选框，则输入区域中的数据在输出表中将进行变换。

步骤6：单击“确定”按钮，即可看到分析的结果，如图22-46所示。

注意：输入区域中数值的个数必须为2的乘幂，比如2、4、6、8、16、32、64、128等，否则会出现错误提示框，如图22-47所示。

图22-45　设置傅里叶分析选项

图22-46　傅里叶分析结果

图22-47　输入区域数值个数错误时的提示框

Excel F-检验双样本方差分析

“F-检验双样本方差”分析工具通过双样本F-检验对两个样本总体的方差进行比较。例如，可在一次游泳比赛中对每两个队的时间样本使用F-检验工具。该工具提供空值假设的检验结果，该假设的内容是：这两个样本来自具有相同方差的分布，而不是方差在基础分布中不相等。

该工具计算F-统计（或F-比值）的F值。F值接近于1，说明基础总体方差是相等的。在输出表中，如果F<1，则当总体方差相等且根据所选择的显著水平“F单尾临界值”返回小于1的临界值时，“P（F≤f）单尾”返回F-统计的观察值小于F的概率Alpha。如果F>1，则当总体方差相等且根据所选择的显著水平“F单尾临界值”返回大于1的临界值时，“P（F≤f）单尾”返回F-统计的观察值大于F的概率Alpha。

下面通过实例说明如何进行F-检验双样本方差分析。

步骤1：将要处理的数据按图22-39所示输入到工作表中。