公司有205件产品需要通过船运出港口,产品的包装箱分为每箱装产品28个、22个、15个、11个和9个等5种规格,现要求用以上5种包装箱装产品,以箱子的空位少为前提,因为空位越多,产品就越容易受到摆晃而损伤。
例如,规格为28的装8箱,那么最后一箱的空位是19,规格为11的装19箱,那么最后一箱的空位是4,假设只有这两种装箱方式,应优先选择后一种。
现在的问题是,如何装箱才能保证每个箱子的剩余空位最少?
解题步骤
人工计算这种装箱问题相当烦琐,而且很难确保找出的解是最优化的。利用规划求解可以快速解决此问题,具体操作步骤如下。
1.根据已知条件在工作表中输入图6.81所示的数据。
2.在 F3 单元格输入公式“=SUMPRODUCT(A2:E2,A3:E3)-G3”,公式的含义是计算规格(每箱中可装产品的件数)乘以箱子数量的乘积之和再减产品数量,从而得到空位的数量。由于当前箱子的数量为0,因此空位将等于产品数量的相反数,效果如图6.82所示。
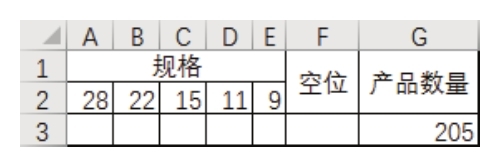
图6.81 输入已知条件
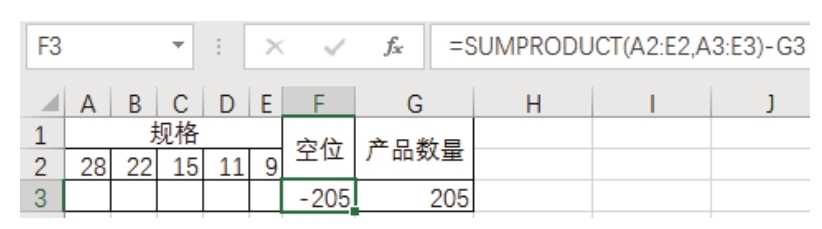
图6.82 设置公式
假设已安装了规划求解,安装过程参考疑难135。
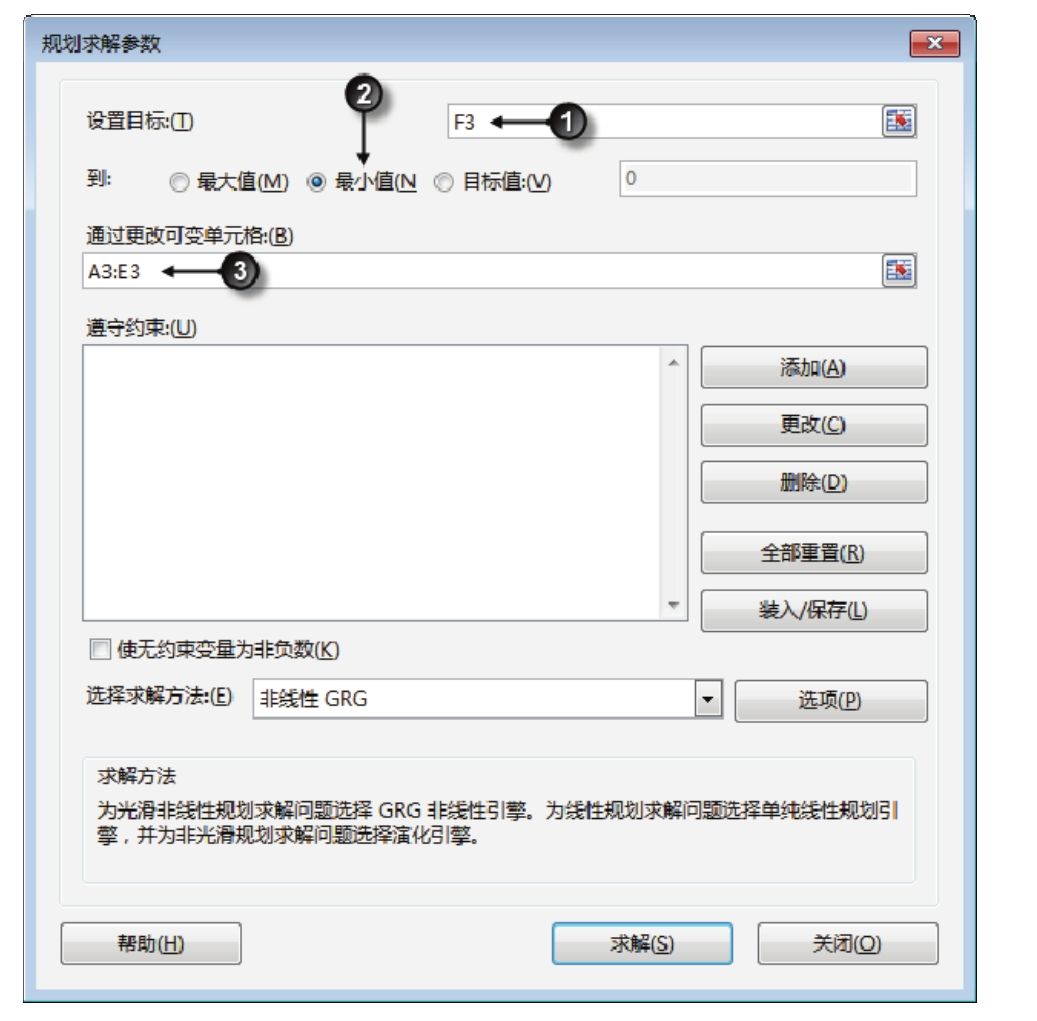
3.单击功能区的“数据”→“规划求解”,从而弹出“规划求解参数”对话框。
4.将目标单元格设置为“F3”,并选择其下方的“最小值”复选框,表示在求解过程中 F3单元格的值最小时停止求解。
5.在“通过更改可变单元格”下方输入“A3:E3”,表示A3:E3区域的值在求解过程中会不断变化,设置界面如图6.83所示。
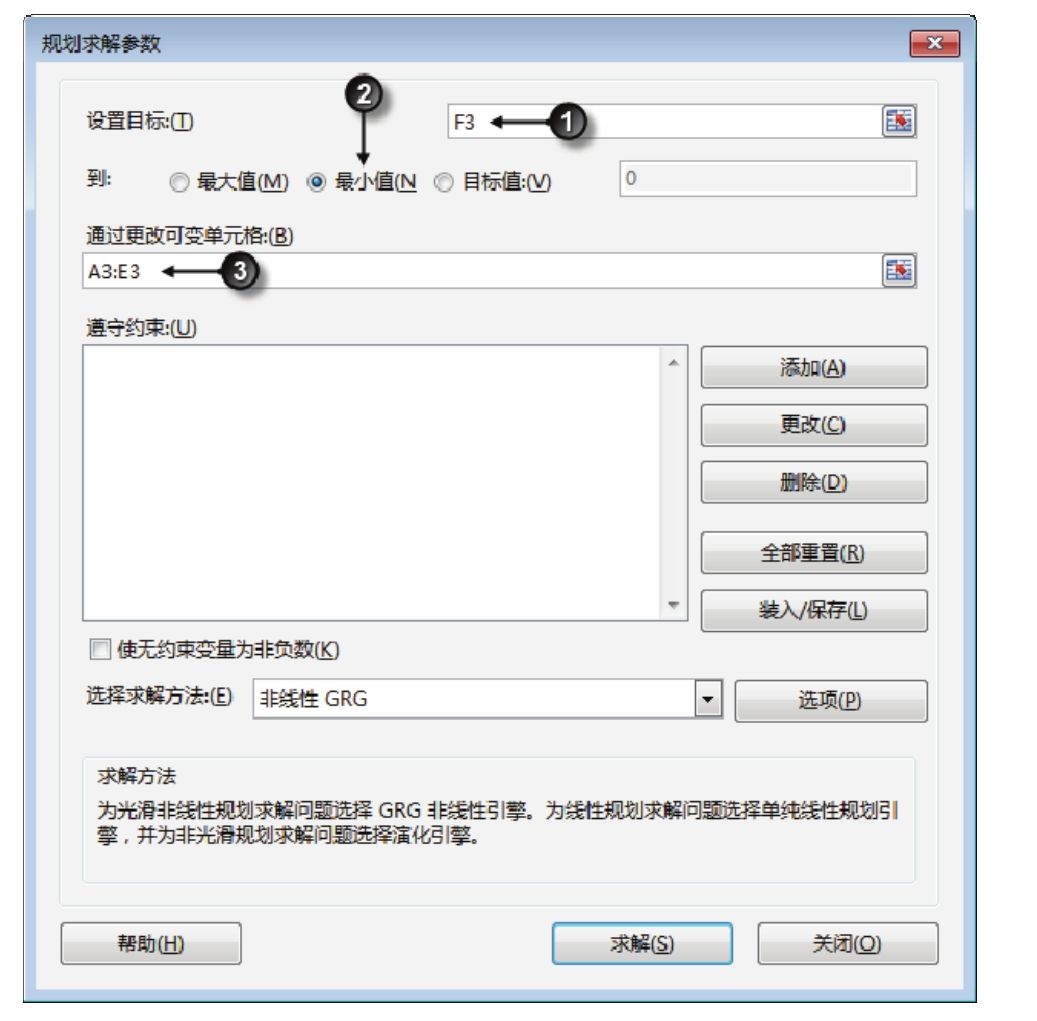
图6.83 设置目标与可变单元格
6.单击右方的“添加”按钮,然后按图6.84所示的方式添加约束条件,此条件表示A3:E3区域只能是整数(箱子的数量不存在小数)。
7.单击“添加约束”对话框中的“添加”按钮,弹出“添加约束”对话框,在对话框中按图6.85的方式设置第二个约束条件,此条件表示A3:E3区域中的值不能是负数。
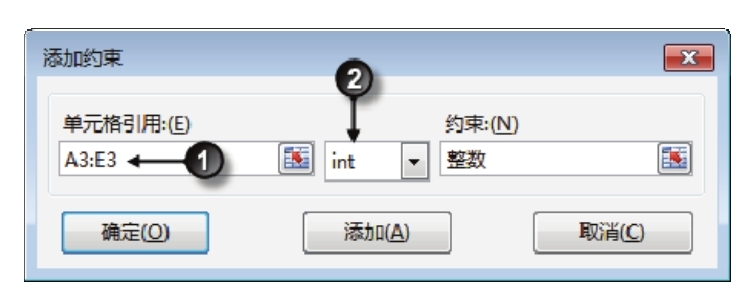
图6.84 添加约束条件一
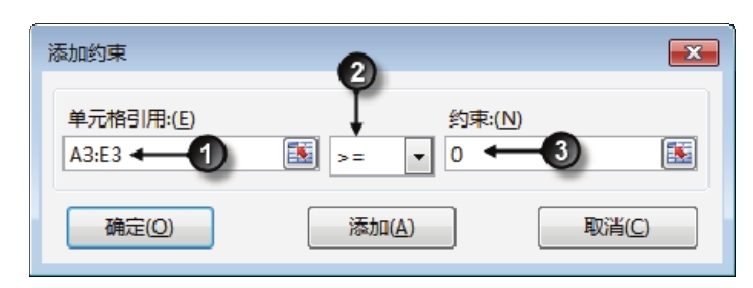
图6.85 添加约束条件二
8.再次单击“添加”按钮,然后按图6.86所示的方式设置约束条件,此条件表示F3单元格的空位数量不能是负数。
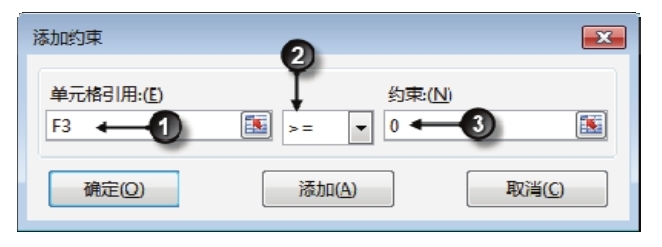
图6.86 添加约束条件三
9.返回“规划求解参数”对话框中,单击“求解”按钮,Excel 得到解后会弹出“规划求解结果”对话框,单击“确定”按钮关闭对话框,然后在工作表中会看到如图6.87所示的结果,其中规格为28的箱子需要7个,规则为11的箱子需要1个,按此方式装箱剩余的空位为2。
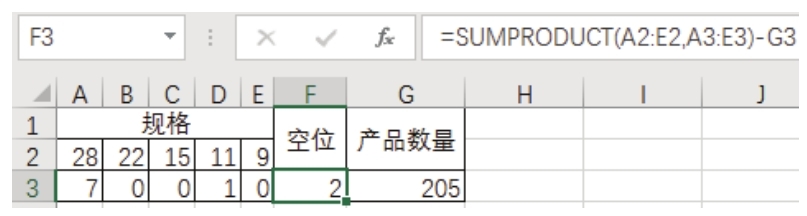
图6.87 最终取得的解
利用公式验算得知上面的计算结果是正确的,但是同样也可以验算得知上面的解并不是最优的,因为规格为11的箱子使用了1个,最后箱子中有两个空位,很显然换成规格为9的箱子可以做到空位为0。
解决这种问题的方法是让公式的计算结果远离0值。因为规划求解其实就是通过一次一次测试的方法查找接近目标的值,本例中的求解目标是大于等于0的最小值,当测试结果越接近0时Excel的测试频率就会越低,往往没有真正找到最优解就停止测试了。而当最优解远离0时,找到最优解的可能性就会大大提升,代价是运算时间更长。
以下步骤可以让规划求解找到最优的解。
10.删除A3:F3的解,然后在H3单元格输入公式“=F3*1000”,此时工作表显示内容如图6.88所示。

图6.88 添加辅助公式
11.单击功能区的“数据”→“规划求解”,弹出如图6.89所示的对话框,对话框中保留了上一次使用的所有参数。
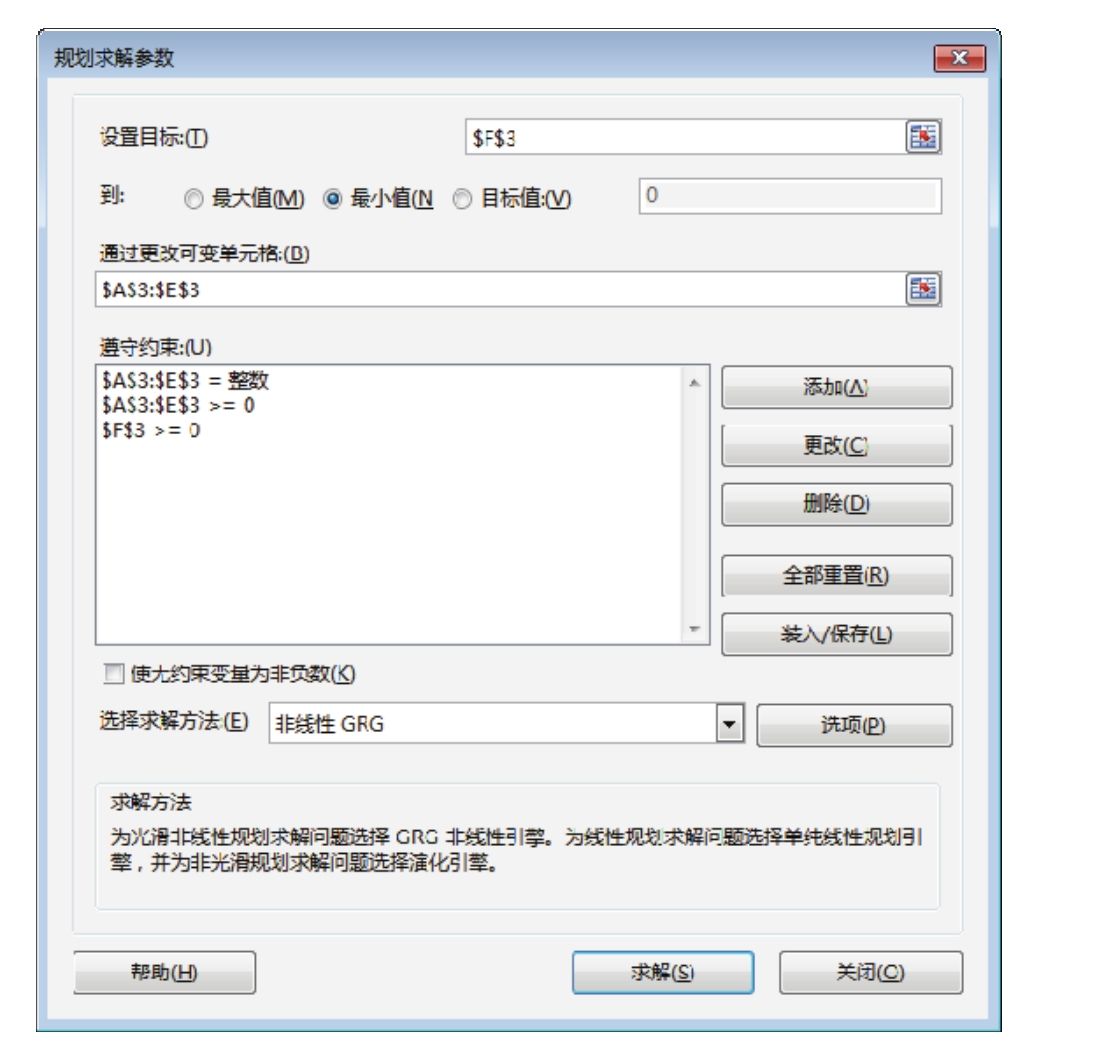
图6.89 保留上次用到的所有参数
12.将目标单元格 F3 修改为 H3,其他参数保持不变,然后单击“求解”按钮,此时得到的结果如图6.90所示。
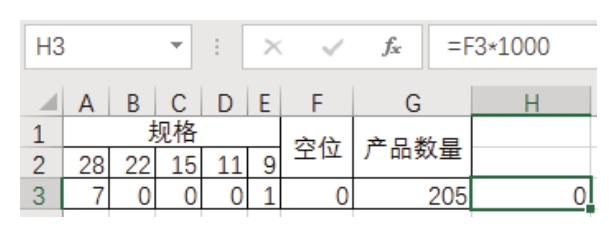
图6.90 优化后的解
知识扩展
1.规划求解主要解决两类问题:一类是解方程那种绝对正确的解,在“规划求解参数”对话框中需要将“目标值”设置为等于某个具体的数值;另一类是求最优的解,要求在多个解中找出最大值或最小值。本例的问题属于第二类。
2.不管问题有多少个解,规划求解工具只列出其中一个解。至于此解是否最优,往往取决于用户设定的约束条件和参数是否正确。
3.并不是最优目标值靠近0时就一定找不到最优的结果,只是说找不到最优解的可能性更大而已。在图6.91和图6.92的测试中,直接将E3单元格的公式计算结果设置为目标,或者在G3中使用辅助公式将E3单元格的值扩大到1000倍后得到的结果都一样。
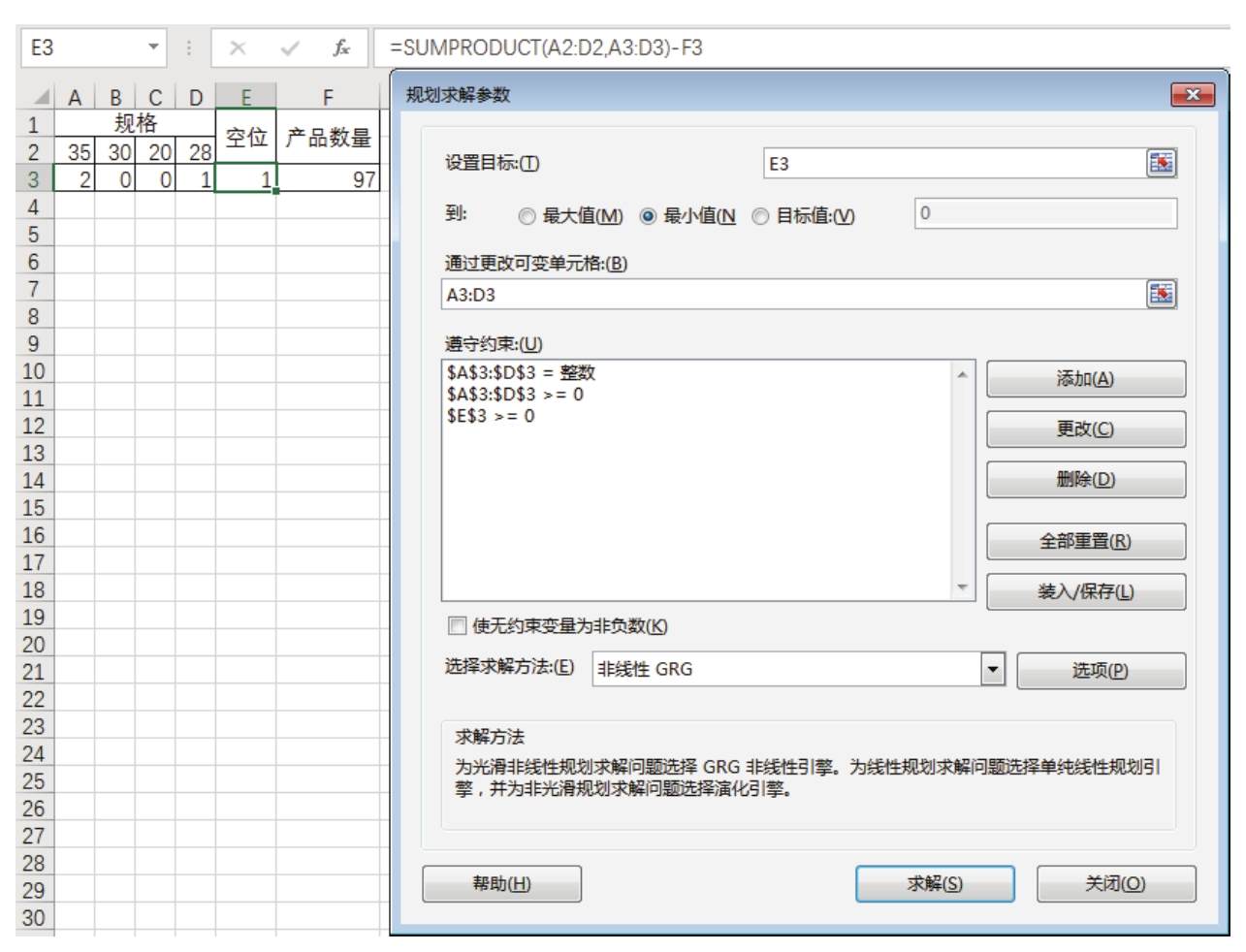
图6.91 直接用E3单元格的公式作为目标求解
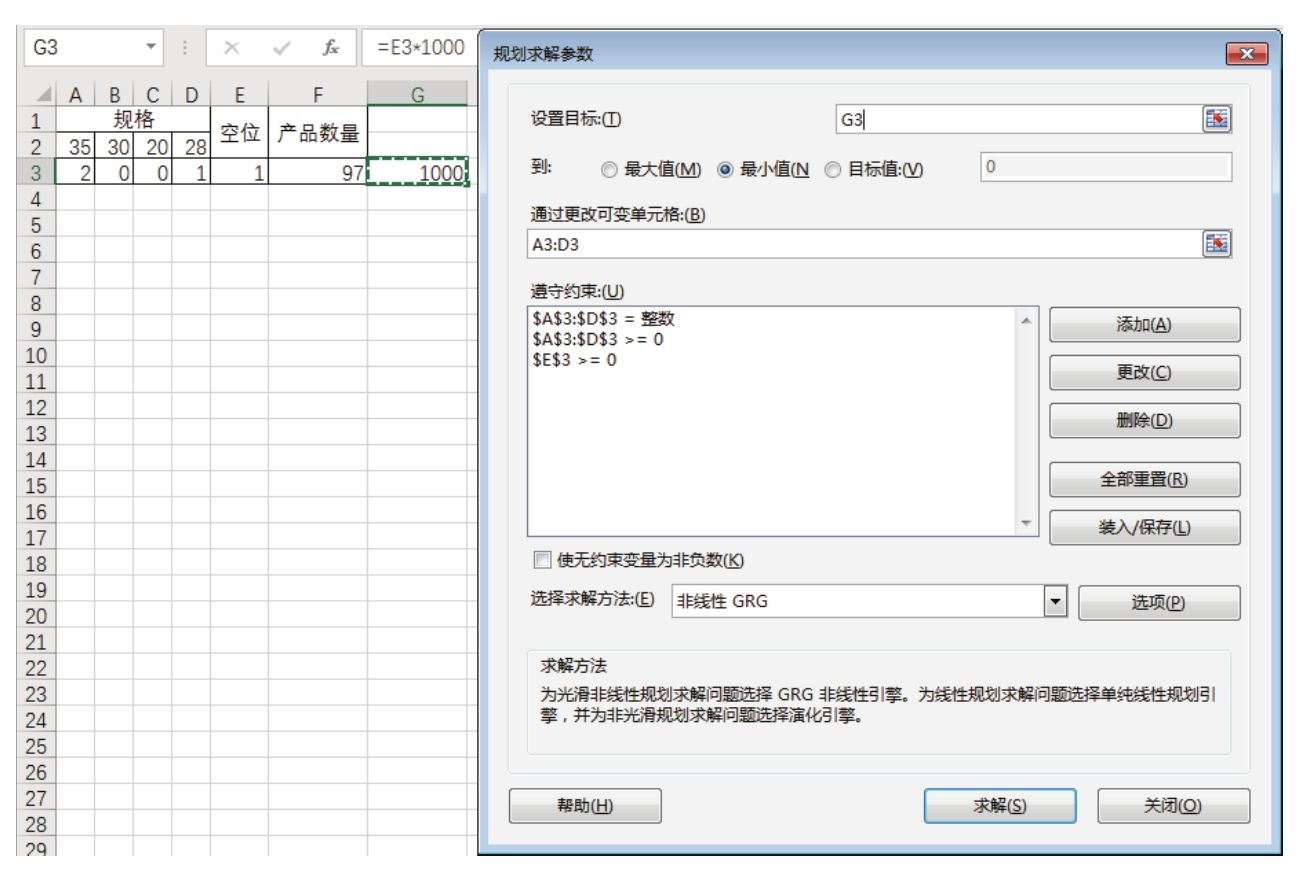
图6.92 将E3单元格的结果扩大到1000倍后再求解
本例中由于第一次就找到了最优解,因此两次求解的结果一致。
判断得到的解是否最优,按上面的方法多试几次,结果一致就表示找到了最优解。