“随机数发生器”分析工具可用几个分布之一产生的独立随机数来填充某个区域。可以通过概率分布来表示一组数据的总体特征。例如,可以使用正态分布来表示人体身高的总体特征,或者使用双值输出的伯努利分布来表示掷币实验结果的总体特征。
下面通过实例说明如何进行随机数发生器分析。
步骤1:打开例子工作表,如图22-56所示。
步骤2:单击“数据”选项卡,然后单击“分析”组中的“数据分析”命令,打开“数据分析”对话框。
步骤3:选中“分析工具”列表中的“随机数发生器”,如图22-57所示。
图22-56 输入将要处理的数据
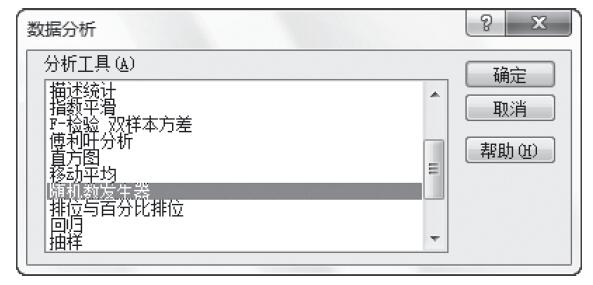
图22-57 选中“分析工具”列表中的“随机数发生器”
步骤4:单击“确定”按钮,打开“随机数发生器”对话框。
步骤5:根据需要设置以下选项,具体设置如图22-58所示。其中一些选项简要介绍如下。
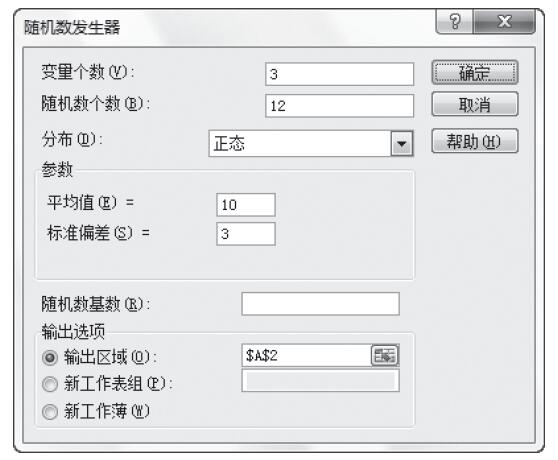
图22-58 设置随机数发生器选项
- 随机数个数:在此输入要查看的数据点个数。每一个数据点出现在输出表的一行中。如果没有输入数字,Excel会在指定的输出区域中填充所有的行。
- 分布:在此选择用于创建随机数的分布方法。
- 均匀:以下限和上限来表征。其变量是通过对区域中的所有数值进行等概率抽取而得到的。普通的应用是在范围0到1之间的均匀分布。Excel 2016共提供了7种随机数的分布方法,分别为均匀、正态、伯努利、二项式、泊松、模式和离散。
- 正态:以平均值和标准偏差来表征。普通的应用是平均值为0,标准偏差为1的标准正态分布。
- 伯努利:以给定的试验中成功的概率(p值)来表征。伯努利随机变量的值为0或1。例如,可以在范围0到1之间抽取均匀分布随机变量。如果变量小于或等于成功的概率,则伯努利随机变量的值为1,否则,随机变量的值为0。
- 二项式:以一系列试验中成功的概率(p值)来表征。例如,可以按照“试验次数”框中指定的个数生成一系列伯努利随机变量,这些变量之和为一个二项式随机变量。
- 泊松:以值λ来表征,λ等于平均值的倒数。泊松分布经常用于表示单位时间内事件发生的次数,例如,汽车到达收费停车场的平均速率。
- 模式:以上界和下界、步长、数值重复率以及序列重复率来表征。
- 离散:以数值及相应的概率区域来表征。在本对话框中给定的输入区域必须包含两列,左边一列包含数值,右边一列为与数值对应的发生概率。所有概率的和必须为1。
- 参数:在此输入用于表征选定分布的数值。
- 随机数基数:在此输入用来构造随机数的可选数值。可以在以后重新使用该数值来生成相同的随机数。
步骤6:单击“确定”按钮,即可看到分析的结果,如图22-59所示。
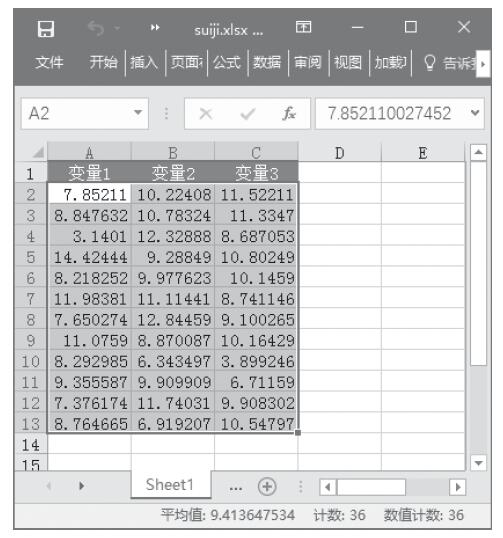
图22-59 随机数发生器分析结果