t-检验工具用于判断每个样本,检验样本总体平均值是否相等。t-检验工具共分为3个工具,分别是平均值的成对二样本分析、双样本等方差假设和双样本异方差假设。
平均值的成对二样本分析
平均值的成对二样本分析可以确定取自处理前后的观察值是否具有相同总体平均值的分布。当样本中出现自然配对的观察值时,可以使用此工具成对检验。在“数据分析”对话框中,选择“t-检验:平均值的成对二样本分析”选项,然后单击“确定”按钮,打开“t-检验:平均值的成对二样本分析”对话框,如图7-99所示。
“平均值的成对二样本分析”对话框中的各项属性设置如下。
- 变量1的区域:需要统计的第1个样本。
- 变量2的区域:需要统计的第2个样本。
- 假设平均差:两个平均值之间的假设差异。
- 标志:指定数据的范围是否包含标签。
- α(A):表示检验的置信水平。
- 输出区域:存放统计结果的单元格区域,可以单击“输出区域”右侧的压缩按钮选择数据区域。
- 新工作表组:新建一个工作表,并将数据分析结果存放在新建工作表中。
- 新工作簿:新建一个工作簿,并将数据分析结果存放在新建工作簿中。
双样本等方差假设
t-检验先假设两个数据集具有相同方差的分布,也称作同方差t-检验。可以使用t-检验来确定两个样本是否具有相同总体平均值的分布。在“数据分析”对话框中,选择“t-检验:双样本等方差假设”选项,然后单击“确定”按钮,打开“t-检验:双样本等方差假设”对话框,如图7-100所示。
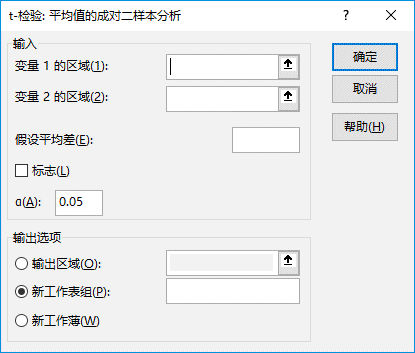
图7-99 “t-检验:平均值的成对二样本分析”对话框
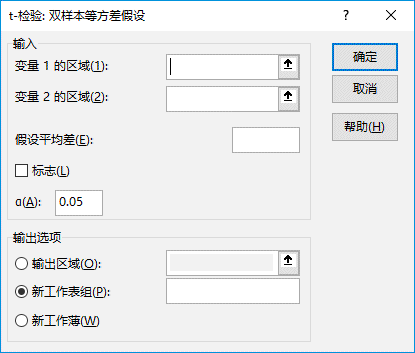
图7-100 “t-检验:双样本等方差假设”对话框
“t-检验:双样本等方差假设”对话框中的各项设置介绍如下。
- 变量1的区域:需要统计的第1个样本。
- 变量2的区域:需要统计的第2个样本。
- 假设平均差:两个平均值之间的假设差异。
- 标志:指定数据的范围是否包含标签。
- α(A):表示检验的置信水平。
- 输出区域:存放统计结果的单元格区域,可以单击“输出区域”右侧的压缩按钮选择数据区域。
- 新工作表组:新建一个工作表,并将数据分析结果存放在新建工作表中。
- 新工作簿:创建一个工作簿,并将数据分析结果存放在新建工作簿中。
双样本异方差假设
双样本异方差假设先假设两个数据集具有不同方差的分布,也称作异方差t-检验。与上面的“等方差”一样,可以使用t-检验来确定两个样本是否具有相同总体平均值的分布。当两个样本存在截然不同的对象时,可使用此检验。在“数据分析”对话框中,选择“t-检验:双样本异方差假设”选项,然后单击“确定”按钮,打开“t-检验:双样本异方差假设”对话框,如图7-101所示。
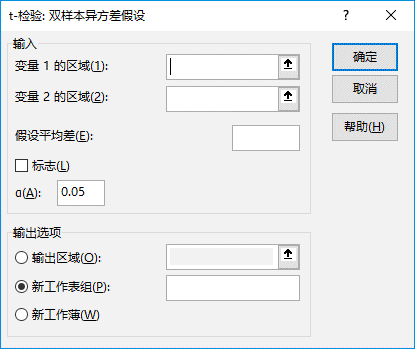
图7-101 “t-检验:双样本异方差假设”对话框
“双样本异方差假设”对话框中的各项设置介绍如下。
- 变量1的区域:需要统计的第1个样本。
- 变量2的区域:需要统计的第2个样本。
- 假设平均差:两个平均值之间的假设差异。
- 标志:指定数据的范围是否包含标签。
- α(A):表示检验的置信水平。
- 输出区域:存放统计结果的单元格区域,可以单击“输出区域”右侧的压缩按钮选择数据区域。
- 新工作表组:新建一个工作表,并将数据分析结果存放在新建工作表中。
- 新工作簿:新建一个工作簿,并将数据分析结果存放在新建工作簿中。
以上简单介绍了3种工具的使用方法,下面通过实例来具体讲解应用技巧。
打开“t-检验分析.xlsx”工作簿,已知两个零件的测试数值,使用“双样本等方差假设分析工具”对测试数据进行分析,具体操作步骤如下所示。
STEP01:切换至“数据”选项卡,然后在“分析”组中单击“数据分析”按钮,打开如图7-102所示的“数据分析”对话框。在“分析工具”列表框中选择“t-检验:双样本等方差假设”选项,然后单击“确定”按钮。
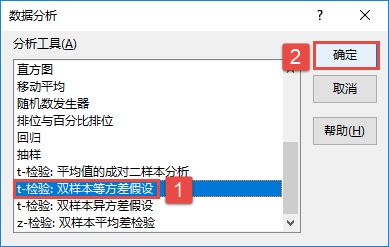
图7-102 选择双样本等方差假设分析工具
STEP02:随后会打开“t-检验:双样本等方差假设”对话框,在“输入”列表区域设置变量1的区域为“$B$2:$B$15”,设置变量2的区域为“$C$2:$C$15”,勾选“标志”复选框,并设置α的值为“0.05”,然后在“输出选项”列表中单击选中“新工作表组”单选按钮,最后单击“确定”按钮,如图7-103所示。
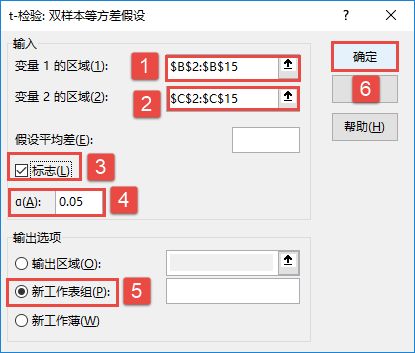
图7-103 设置属性
STEP03:此时,工作表中会显示“t-检验:双样本等方差假设”的分析结果,如图7-104所示。
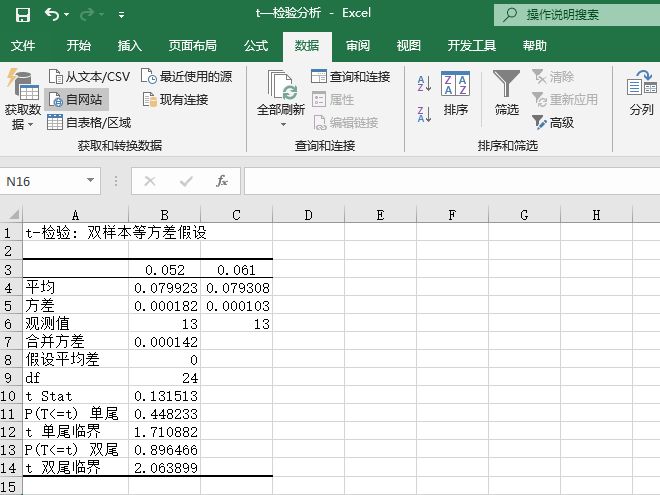
图7-104 “t-检验:双样本等方差假设”分析结果