SERIESSUM函数的功能是计算基于幂级数展开式的幂级数之和。许多函数可由幂级数展开式近似地得到。其语法如下:
SERIESSUM(x,n,m,coeffi cients)
其中,x参数为幂级数的输入值;参数n为参数x的首项乘幂;m参数为级数中每一项的乘幂n的步长增加值;coefficients参数为一系列与参数x各级乘幂相乘的系数,它的数目决定了幂级数的项数,如果参数coefficients中有3个值,幂级数中将有3项。
在该函数的功能提到一个概念——幂级数。幂级数形式上是个无穷多项式,通常依变量x的升幂顺序来表示。幂级数是微积分中的重要内容,许多重要的函数可以幂级数表示,而幂级数全体也代表了相当广泛的函数类别。下面通过实例详细讲解该函数的使用方法与技巧。
根据幂级数展开式求解函数y=sinx在x=π/3的近似函数值,并将该近似值与直接求解的结果进行比较,其中sinx的级数展开式为:sinx=x-x3/3!+x5/5!-x7/7!+……。打开“SERIESSUM函数.xlsx”工作簿,本例的原始数据如图14-64所示。具体操作步骤如下。
图14-64 原始数据
STEP01:选中B8单元格,在编辑栏中输入公式“=SIN(PI()/3)”,然后按“Enter”键返回,即可计算出y=sinx在x=π/3的准确结果,如图14-65所示。
STEP02:选中B9单元格,在编辑栏中输入公式“=SERIESSUM(B2,1,2,B3:B6)”,然后按“Enter”键返回,即可计算出y=sinx在x=π/3的级数展开数值,如图14-66所示。
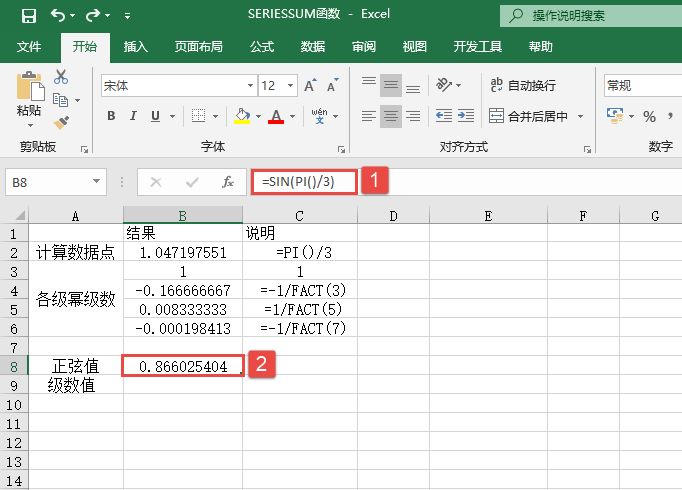
图14-65 计算y=sinx在x=π/3的准确结果
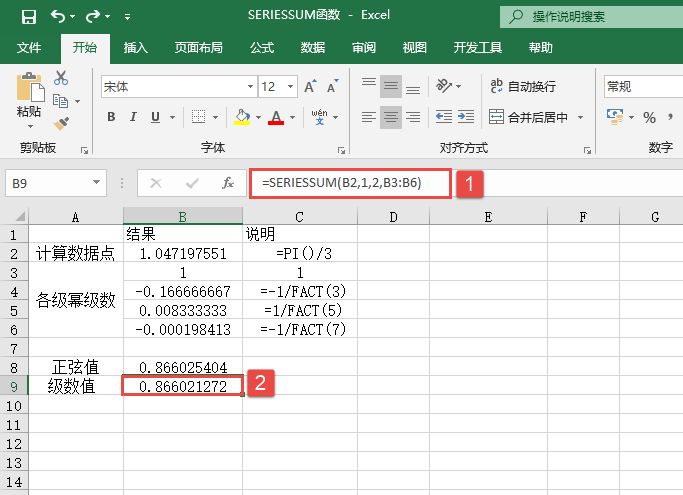
图14-66 计算函数的级数值
SERIESSUM函数主要用来求解函数在某一点的近似值。对该函数来说,如果任一参数为非数值型,SERIESSUM函数将会返回错误值“#VALUE!”。